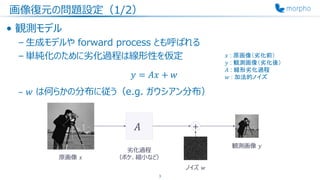
今回は、最適化アルゴリズムとノイズ除去アルゴリズムを組み合わせた非線形画像復元のフレームワークを紹介します。 画像復元とは、劣化した観測画像からクリーンな未知の原画像を推定するタスクであり、ボケ除去や超解像、インペインティングなど幅広い問題を内包しています。 一般に、観測画像は原画像の情報を十分に持っていないので、原画像の推定は劣決定となり解が一意に定まりません。 そのため、原画像に関する事前知識（Prior）を与えた最適化問題として画像復元を定式化し、解空間に制約を与えることがよく行われます。 制約付き最適化問題の解放として、ADMM（Alternating Direction Method of Multipliers; 交互方向乗数法）が有名です。 ADMMは非 Deep Learning 系の反復アルゴリズムの一種であり、もとの問題を複数の小さな部分問題に分割し順番に更新することで最適化を実現します。 また、部分問題が単純であれば一次収束が保証されるメリットがあります。 ------------------ Morpho, Inc. Website: https://www.morphoinc.com/ Tech Blog: https://techblog.morphoinc.com/

1. 紹介論文：
S. H. Chan, X. Wang, and O. A. Elgendy,
“Plug-and-Play ADMM for Image Restoration:
Fixed Point Convergence and Applications”
CTO室 長山知司

2. 概要
• 汎用のノイズ除去アルゴリズム（デノイザ）を使って画像復元を実現
– デノイザはパッチベース（BM3Dなど）やNNベース（DnCNNなど）
の種類を問わない
– 最適化理論の背景により収束性が保証される
• Contributions
– 拡張した Plug-and-Play ADMM (PnP-ADMM) の枠組みを提案
– 有界デノイザと呼ばれるクラスを導入し、PnP-ADMM が適切に動作する
デノイザの条件を明確化
• 従来法より幅広い種類のデノイザが利用できるように
– ポリフェーズ分解に基づく単一画像超解像の高速実装法を提案
1

3. I. Introduction
2

4. 画像復元の問題設定（1/2）
• 観測モデル
– 生成モデルや forward process とも呼ばれる
– 単純化のために劣化過程は線形性を仮定
𝑦 = 𝐴𝑥 + 𝑤
– 𝑤 は何らかの分布に従う（e.g. ガウシアン分布）
3
𝑥 : 原画像（劣化前）
𝑦 : 観測画像（劣化後）
𝐴 : 線形劣化過程
𝑤 : 加法的ノイズ
𝐴 +
原画像 𝑥
ノイズ 𝑤
観測画像 𝑦
劣化過程
（ボケ、縮小など）

5. 画像復元の問題設定（2/2）
• 復元モデル（MAP推定）
– 確率モデルによって観測画像 𝑦 から 原画像 𝑥 を推定
– 最適化問題として定式化
ො𝑥 = argmax 𝑥 𝑝 𝑦 𝑥 𝑝 𝑥
= argmin 𝑥 𝑓 𝑥 + 𝜆𝑔 𝑥
• 𝑓 𝑥 : データ忠実項
– 劣化させた推定値と観測画像との類似度を表す
– 二乗誤差 𝐴𝑥 − 𝑦 2 がよく用いられる
• 𝑔 𝑥 : 正則化項
– 復元画像の解空間に対する制約を表す
– L1 ノルムやTotal Variation (TV) などが画像処理では代表的
4
ො𝑥 : 𝑥 の推定値（復元画像）
𝑝 𝑦 𝑥 : 尤度関数
𝑝 𝑥 : 𝑥 の事前分布（Prior）
𝑓 𝑥 ≔ − log 𝑝 𝑦 𝑥
𝜆𝑔 𝑥 ≔ − log 𝑝 𝑥

6. ADMMの概要（1/4）
• MAP推定を解くアルゴリズムとして ADMM が有名
– Alternating Direction Method of Multipliers; 交互方向乗数法
• 利点
– 直接的に最適化が困難な問題を 𝑓, 𝑔 それぞれの最適化に分解できる
– 適切な設定のもとで一次収束が保証
5
𝜌 𝑘 > 0 とし、初期値 𝑥 0 , 𝑣 0 , 𝑢 0 を設定する。
以下の更新式を停止条件が満たされるまで反復：
𝑥 𝑘+1
∈ argmin 𝑥 𝑓 𝑥 +
𝜌 𝑘
2
𝑥 − 𝑣 𝑘
+ 𝑢 𝑘 2
𝑣 𝑘+1
∈ argmin 𝑣 𝜆𝑔 𝑣 +
𝜌 𝑘
2
𝑥 𝑘+1
− 𝑣 + 𝑢 𝑘 2
𝑢(𝑘+1)
= 𝑢 𝑘
+ 𝑥 𝑘+1
− 𝑣 𝑘+1
このとき、ある種の条件のもとで 𝑥 𝑘 は最適解に近づく

7. ADMMの概要（2/4）
• ラフな導出(1/2)
– 𝑓, 𝑔 を凸関数と仮定する
– 変数 𝑣 を導入し、制約付き最適化問題に置き換える
• minimize 𝑥,𝑣 𝑓 𝑥 + 𝜆𝑔 𝑣 s. t. 𝑥 − 𝑣 = 0
– 拡張ラグランジアン 𝐿 𝜌(𝑥, 𝑣, 𝜏) を定義（𝜏 : ラグランジュ乗数, 𝜌 > 0）
• 𝐿 𝜌 𝑥, 𝑣, 𝜏 ≔ 𝑓 𝑥 + 𝜆𝑔 𝑣 + 𝜏 𝑇
𝑥 − 𝑣 +
𝜌
2
𝑥 − 𝑣 2
• 𝑥∗
, 𝑣∗
∈ argmin 𝑥,𝑣 max 𝜏 𝐿 𝜌(𝑥, 𝑣, 𝜏) はもとの最適化問題の解
• 𝑓, 𝑔 が凸ならば 𝐿 𝜌 は (𝑥, 𝑣) に関して強凸（min 𝑥,𝑣 𝐿 𝜌(𝑥, 𝑣, 𝜏) の解は唯一）
– 主変数 𝑥, 𝑣 と双対変数 𝜏 を交互に最適化（双対上昇法）
• 𝑥 𝑘+1
, 𝑣 𝑘+1
= argmin(𝑥,𝑣) 𝐿 𝜌 𝑥, 𝑣, 𝜏 𝑘
• 𝜏 𝑘+1
= 𝜏 𝑘
+ 𝜌 𝑥 𝑘+1
− 𝑣 𝑘+1
6

8. ADMMの概要（3/4）
• ラフな導出(2/2)
– 𝑢 ≔ 𝜏/𝜌 に変換（𝑢 : 規格化したラグランジュ乗数）
• 𝑥 𝑘+1
, 𝑣 𝑘+1
= argmin(𝑥,𝑣) 𝑓 𝑥 + 𝜆𝑔 𝑣 +
𝜌
2
𝑥 − 𝑣 + 𝑢 𝑘 2
• 𝑢 𝑘+1
= 𝑢 𝑘
+ 𝑥 𝑘+1
− 𝑣 𝑘+1
– 同時最適化の箇所を分解
• 𝑥 𝑘+1
= argmin 𝑥 𝑓 𝑥 +
𝜌
2
𝑥 − 𝑣 𝑘
+ 𝑢 𝑘 2
• 𝑣 𝑘+1
= argmin 𝑣 𝜆𝑔 𝑣 +
𝜌
2
𝑥 𝑘+1
− 𝑣 + 𝑢 𝑘 2
• 𝑢 𝑘+1
= 𝑢 𝑘
+ 𝑥 𝑘+1
− 𝑣 𝑘+1
7

9. ADMMの概要（4/4）
• 収束定理（大域的収束性）
– 𝑓, 𝑔 に与える制約や 𝜌 𝑘 の違いなどにより多数のヴァリエーションが存在
– ここでは、次の条件を仮定する：
1. 𝑓: ℝ 𝑛
→ ℝ, 𝑔: ℝ 𝑛
→ ℝ はそれぞれプロパー1かつ下半連続2な最小値をもつ凸関数
2. 任意の 𝑘 ∈ ℕ について 𝜌 𝑘 = 𝜌 > 0
– 仮定のもとで次の定理が成り立つ[2]
8
1 定義域が空ではない i.e. dom 𝑓 ≠ ∅
2 任意の𝑥0 ∈ dom 𝑓について𝑓 𝑥0 ≤ liminf
𝑥→𝑥0
𝑓 𝑥
3 𝑓∗ −𝑢 + 𝑔∗(𝑢/𝜆) ： 関数 𝑓 𝑥 + 𝜆𝑔(𝑥) の凸共役
残差収束 : 𝑘 → ∞ のとき 𝑥 𝑘
− 𝑣 𝑘
→ 0
目的収束 : 𝑘 → ∞ のとき 𝑓 𝑥 𝑘
+ 𝜆𝑔 𝑣 𝑘
→ min
𝑥, 𝑣
𝑓 𝑥 + 𝜆𝑔 𝑣 s. t. 𝑥 = 𝑣
双対変数収束3 : 𝑘 → ∞ のとき 𝑢 𝑘
→ argmin 𝑢 𝑓∗
−𝑢 + 𝑔∗
(𝑢/𝜆)

10. Plug-and-Play Schemeの概要（1/3）
• ADMMは最適化問題を分解しただけなので、𝑓 と 𝑔 それぞれの
最適化が難しければ実用的ではない
– そのため、正則化項 𝑔 の選択には強い制限がかかる
– データ忠実項 𝑓 については、そもそも最適化が容易なことが多いので
深く考えなくとも良い（e.g. MSE）
• ここで、𝑔 についての argmin を作用素として捉えてみる
– 作用素 𝒟 𝑔 は Proximity operator (Prox) と呼ばれる4
– 正則化項（Prior）𝑔 により 𝒟 𝑔 が定まる構造
9
𝑣 𝑘+1
∈ 𝒟 𝑔 𝑥(𝑘+1)
− 𝑢 𝑘
𝒟 𝑔 𝑥 ≔ argmin 𝑣 𝜆𝑔 𝑣 + 𝜌/2 ⋅ 𝑥 − 𝑣 2
4 通常は 𝑔 の凸性を要求するが、ここでは仮定しない。
また、標準的な記法では 𝒟 𝑔 = Prox 𝜆/𝜌 𝑔 と表される。

11. Plug-and-Play Schemeの概要（2/3）
• Plug-and-Play Schemeの基本的なアイディア
– Prior と Prox の因果関係を逆転
• Plug-and-Play ADMM（PnP-ADMM）[3]
– ℱ, 𝒟 はユーザが定義する写像
– 尤度関数とPriorはそれぞれ ℱ, 𝒟 から implicit に導かれるものとして扱う
10
初期値 𝑥 0 , 𝑣 0 , 𝑢 0 を設定する。
以下の更新式を停止条件が満たされるまで反復：
𝑥 𝑘+1
= ℱ 𝑣 𝑘
− 𝑢 𝑘
𝑣 𝑘+1
= 𝒟 𝑥 𝑘+1
+ 𝑢 𝑘
𝑢(𝑘+1)
= 𝑢 𝑘
+ 𝑥 𝑘+1
− 𝑣 𝑘+1
通常のADMM: Prior を定義 → 対応する Prox が定まる
Plug-and Play Scheme: Prox を定義 → 対応する Prior が定まる

12. Plug-and-Play Schemeの概要（3/3）
• ノイズ除去アルゴリズムとしての Prox
– ADMMの正則化項 𝑔 には画像を滑らかにする Prior を選ぶことが多い
• TV正則化やTikhonov 正則化など
– つまり、𝑔 に対応する Prox はノイズ除去の作用をもつと解釈できる
• 例えば、Tikhonov 正則化 𝑔 𝑣 = 𝑄𝑣 2
2
（𝑄 は畳み込み行列）
に対応する Prox は Wienerフィルタ[4; Theorem 3.1]
– この類推より、PnP-ADMM の写像 𝒟 をノイズ除去アルゴリズム
（デノイザ）と呼ぶ
• 既存のデノイザを柔軟に組み込めるメリット
• 先行研究ではNon-local means、 BM3D、K-SVD, TVなどが
用いられている[3,5,6]
11

13. II. 提案アルゴリズム
（不動点収束 PnP-ADMM）
12

14. PnP-ADMM の課題
• 一般のデノイザは非線形かつClosed form を持たないので、
次のような課題がある：
1. アルゴリズムの収束性
• 古典的なアプローチでは 𝑔 𝑥 が下半連続かつプロパーな凸関数であれば
収束する。また、非凸関数でも収束する十分条件がいくつか示されているが、
一般のデノイザに対しては知られていない
2. 対応するPriorの存在・具体形
3. 実装
• Inversion mapの高速な実装が応用上必須
• また、Priorによっては 𝑥 = 𝑣 の制約を一般化する必要がある（𝐴𝑥 = 𝐵𝑣 など）
• 提案法は (1.) と (3.) の解決を目的とする
13

15. 提案アルゴリズム
• 従来法からの変更点
– 𝜌 𝑘 を増加させるパラメータ 𝛾 𝑘 を導入
– デノイザ 𝒟 𝜎 𝑘
の強度をステップごとに更新
𝜎 𝑘 ≔ 𝜆/𝜌 𝑘 はデノイザの強度パラメータ（ガウシアンノイズの偏差とは無関係で良い）
14
𝛾 𝑘 ≥ 1, 𝜌0 > 0 とし、初期値 𝑥 0
, 𝑣 0
, 𝑢 0
を設定する。
以下の更新式を停止条件が満たされるまで反復：
𝑥 𝑘+1
= argmin 𝑥 𝑓 𝑥 +
𝜌 𝑘
2
𝑥 − 𝑣 𝑘
− 𝑢 𝑘 2
𝑣 𝑘+1
= 𝒟 𝜎 𝑘
𝑥 𝑘+1
+ 𝑢 𝑘
𝑢(𝑘+1)
= 𝑢 𝑘
+ 𝑥 𝑘+1
− 𝑣 𝑘+1
𝜌 𝑘+1 = 𝛾 𝑘 𝜌 𝑘

16. パラメータ 𝜌 𝑘 の更新方法
• 𝑘 → ∞ のとき十分大きい値になるように設定
– 𝜌 𝑘 が小さいと 𝑥 = 𝑣 の制約が弱まり収束しないおそれがある
• 論文では２種類提案
1. 単調更新ルール
• 𝛾 > 1 とし、𝜌 𝑘+1 = 𝛾𝜌 𝑘 の規則で更新する
2. 適応的更新ルール
• 相対的残差を次のように定義する：
Δ 𝑘+1 ≔
1
𝑛
𝑥 𝑘+1
− 𝑥 𝑘
2
+ 𝑣 𝑘+1
− 𝑣 𝑘
2
+ 𝑢 𝑘+1
− 𝑢 𝑘
2
• 𝜂 ∈ 0,1 , 𝛾 > 1 とし、次の規則に従って更新する：
1. Δ 𝑘+1 ≥ 𝜂Δ 𝑘 ならば 𝜌 𝑘+1 = 𝛾𝜌 𝑘 とする
2. Δ 𝑘+1 < 𝜂Δ 𝑘 ならば 𝜌 𝑘+1 = 𝜌 𝑘 とする
15

17. 提案アルゴリズムの収束性（1/3）
• 非拡大デノイザ（Non-expansive denoiser）
– 伝統的なADMMの収束定理ではデノイザの非拡大性が必要
• 非拡大写像 𝒟 𝜎: ∀𝑥 ∀𝑦 ∃𝜅 ∈ 0,1 𝒟 𝜎 𝑥 − 𝒟 𝜎 𝑦 ≤ 𝜅‖𝑥 − 𝑦‖
• 言い換えれば リプシッツ定数 ≤ 1
– 任意の 𝑥, 𝑦 のペアで成り立つ必要があるため、証明は難しい
• 一般のデノイザに求める性質としては制約が強すぎる
• 直感的に非拡大に見えるアルゴリズムでも反例が見つかる場合がある（e.g. NLM）
16
NLMの反例（𝜅 = 1.1775）
引用：[1; Fig. 10]

18. 提案アルゴリズムの収束性（2/3）
• 有界デノイザ（Bounded Denoiser）
– 非拡大デノイザよりもう少し緩い制約のクラスを考えたい
– 任意の 𝑥 ∈ ℝ 𝑛
に対して、以下の関係を満たすデノイザ 𝒟 𝜎 を
有界デノイザと定義：
𝒟 𝜎 𝑥 − 𝑥 2
/𝑛 ≤ 𝜎2
𝐶
• 𝐶 は 𝑛 と 𝜎 に無関係な定数
• 加法的ノイズのエネルギーの変化量が、デノイズの前後で一定の範囲内に収まる性質
• 𝜎 → 0 のとき 𝒟 𝜎 が恒等写像に収束することを要求
17

19. 提案アルゴリズムの収束性（3/3）
• 定理（PnP-ADMMの不動点収束性）
– 単調更新、適応的更新のいずれでも成立
– ※不動点の存在と収束を保証しているが、最適解との関係は述べていない
• 大域的収束性とは相補的な関係
• もし 𝑓, 𝒟 𝜎 が大域的収束性も同時に満たすならば、 𝑥(𝑘)
が最適解 𝑥∗
に
収束することが言える
18
5 任意の𝑥 ∈ 0,1 𝑛
で勾配が存在し ∇𝑓 𝑥 < ∞を満たす
𝑓 ∶ 0,1 𝑛
→ ℝ を有界勾配5 の関数、𝒟 𝜎 を有界デノイザとする。
このときPnP-ADMMの更新式は不動点収束する。すなわち、
(𝑥∗
, 𝑣∗
, 𝑢∗
) が存在し 𝑘 → ∞ のとき
𝑥 𝑘
− 𝑥∗
2
→ 0, 𝑣 𝑘
− 𝑣∗
2
→ 0, 𝑢 𝑘
− 𝑢∗
2
→ 0
が成り立つ。
また、𝑥 𝑘
→ 𝑣 𝑘
も同時に成立する

20. 停止条件
• 変数 𝑥 𝑘
, 𝑣 𝑘
, 𝑢 𝑘
の相対残差を基準
– 論文では二種類提案（tol: 許容誤差）
1. 相対残差の和（Δ 𝑘+1 ≤ tol）
2. 相対残差の最大値（max 𝜀1, 𝜀2, 𝜀3 ≤ tol/3）
– 𝜀1 ≔ 𝑥 𝑘+1 − 𝑥 𝑘
2
/ 𝑛,
– 𝜀2 ≔ 𝑣 𝑘+1 − 𝑣 𝑘
2
/ 𝑛,
– 𝜀3 ≔ 𝑢 𝑘+1 − 𝑢 𝑘
2
/ 𝑛
• tol を極端に小さくする必要はない
– 経験的に tol ≈ 10−3
程度で十分
19
※実験のデノイザはBM3Dを使用
引用：[1; Fig. 1]

21. 初期パラメータ 𝜌0
• 調整が必要だが、𝜌0 ∈ 10−5
, 10−2
程度でうまくいく
– 右図は 𝜌0 ∈ [10−4
, 100
] の振る舞い
• 赤：オリジナル、青：単調、黒：適応的
• オリジナルのPnP-ADMMと比較：
– 広い範囲の 𝜌0 で動作する
• オリジナルは𝜌0 = 1 でベストを達成、
𝜌0 ≤ 10−2
で非常に悪化
– チューニングを行えば必ずオリジナルよりも
高いPSNRを達成可能
• オリジナルは提案法で 𝛾 𝑘 = 1 とした
特殊ケースに対応
20
※実験のデノイザはBM3Dを使用
引用：[1; Fig. 3]

22. 初期画像
• 初期値 𝑥(0)
, 𝑣 0
, 𝑢 0
は最終的なPSNRに
あまり影響を与えない
– 0,1 𝑛
の一様分布に従う 𝑥 0
を100個
使って実験（右図）
• 𝑣 0
= 𝑥 0
, 𝑢 0
= 0
– 極限での標準偏差は 0.0059 dB
• PSNRは99.7%(3シグマ)の確率で
平均から ±0.0176 dB の範囲に収まる
21
※実験のデノイザはBM3Dを使用
引用：[1; Fig. 3]

23. III. 応用例
22

24. 超解像（1/7）
• Forward モデル
– アンチエイリアス & サブサンプル
• 更新ルール
– 𝑥 の更新式は closed form で与えられる
– 𝐺 ≔ 𝑆𝐻
23
𝑓 𝑥 = 𝑆𝐻𝑥 − 𝑦 2
𝑆 ∈ ℝ 𝑚×𝑛
: バイナリサブサンプリング行列
𝐻 ∈ ℝ 𝑛×𝑛
: アンチエイリアシング（畳み込み行列）
𝑥 𝑘+1
= 𝐺 𝑇
𝐺 + 𝜌𝐼 −1
𝐺 𝑇
𝑦 + 𝜌 𝑣 𝑘
− 𝑢 𝑘
𝑣 𝑘+1
= 𝒟 𝜎 𝑘
𝑥 𝑘+1
+ 𝑢 𝑘

25. 超解像（2/7）
• 高速実装化（1/3）
– 𝑥 𝑘
の更新は毎回 𝑛 × 𝑛 の逆行列の計算が必要で非効率
– Sherman-Morrison-Woodburyの行列恒等式を適用
• より小さい 𝑚 × 𝑚 の逆行列計算のみを含む形式に変形
24
𝑥 𝑘+1
= 𝜌−1
𝑏 𝑘
− 𝜌−1
𝐺 𝑇
𝜌𝐼 + 𝐺𝐺 𝑇 −1
𝐺𝑏 𝑘
𝑏 𝑘
≔ 𝐺 𝑇
𝑦 + 𝜌 𝑣 𝑘
− 𝑢 𝑘

26. 超解像（3/7）
• 高速実装化（2/3）
– 結局 𝜌𝐼 + 𝐺𝐺 𝑇 −1
の計算は避けられない
– 𝐺𝐺 𝑇
= 𝑆𝐻𝐻 𝑇
𝑆 𝑇
は アップサンプル-フィルタ-ダウンサンプルの構造
→ ポリフェーズ分解が可能
• アップサンプル → フィルタの処理をフィルタ → アップサンプルの順に入れ替え可能
– この関係は novel identity と呼ばれる
• フィルタ長を短くできるメリット
25
෩𝐻 𝑘 𝑧 : 𝐻𝐻 𝑇 に対応するフィルタ（z-domain）
↑ 𝐾 : アップサンプラ
↓ 𝐾 : ダウンサンプラ
引用：[1; Fig. 5]

27. 超解像（4/7）
• 高速実装化（3/3）
– 𝑥 𝑘
の更新式の比較
• 青：共役勾配法による解法（反復法）
• 赤 : 高速実装（Closed form）
• 横軸：共役勾配法の反復回数
– 高速実装版はFourierドメインで
フィルタリング
26
引用：[1; Fig. 6]

28. 超解像（5/7）
• 実験A: グレースケール超解像
– 右上図の10枚の画像をGTとする
• サイズ 256x256 or 512x512
– デノイザはBM3D
– 4パターンの設定で実験（右下表）
• 𝐻 は bicubic or ガウスボケ
• 𝐾 : サンプリングファクタ
27
引用：[1; Fig. 7]
引用：[1, Table 1]

29. 超解像（6/7）
• 実験Aの結果
– パッチベースや
NNベースと比較しても
良好な結果
– 適応的更新よりも
単調更新のほうが
若干良いPSNR
28
Ours-M : 単調更新
Ours-A : 適応的更新
Ours-M* : 単調更新、復元モデルの
𝐻 をbicubic とする
引用：[1, Table 2]

30. 超解像（7/7）
• 実験B: カラー画像超解像
– デノイザ：BM3D
– 他手法と比べてわずかに
エッジがシャープ
– ハロー効果も少なく見える
– DCNNにPSNRで劣っている
• train-freeアルゴリズムなので
仕方ない一面はある
29
引用：[1; Fig. 8]

31. Reference
• [1] S. H. Chan, X. Wang, and O. A. Elgendy, “Plug-and-Play ADMM for Image Restoration: Fixed
Point Convergence and Applications,” arXiv:1605.01710[cs], Nov. 2016.
• [2] S. Boyd, “Distributed Optimization and Statistical Learning via the Alternating Direction Method of
Multipliers,” FNT in Machine Learning, vol. 3, no. 1, pp. 1–122, 2010.
• [3] S. V. Venkatakrishnan, C. A. Bouman, and B. Wohlberg, “Plug-and-Play priors for model based
reconstruction,” in 2013 IEEE Global Conference on Signal and Information Processing, Austin, TX,
USA, 2013, pp. 945–948.
• [4] A. Murli, L. D'Amore and V. De Simone, "The Wiener filter and regularization methods for image
restoration problems," Proceedings 10th International Conference on Image Analysis and Processing,
Venice, Italy, 1999, pp. 394-399, doi: 10.1109/ICIAP.1999.797627.
• [5] A. Rond, R. Giryes, and M. Elad, “Poisson Inverse Problems by the Plug-and-Play scheme,”
arXiv:1511.02500[cs, math], Nov. 2015.
• [6] S. Sreehari, S. V. Venkatakrishnan, B. Wohlberg, L. F. Drummy, J. P. Simmons, and C. A.
Bouman, “Plug-and-Play Priors for Bright Field Electron Tomography and Sparse Interpolation,” IEEE
Trans. Comput. Imaging, pp. 1–1, 2016.
30