1. An Inverse Power Method for
Nonlinear
Eigenproblems with Applications in
1-Spectral Clustering and Sparse PCA
NIPS 2010, 1133
江原 遥
@niam
12/26
1

2. 全体の流れ
選んだ理由：
•行列やグラフの話が俯瞰できそう？
• 応用としての目的 •逆べき乗法だからAlgorithmは複雑
じゃないだろう．
– p-Laplacian法というGraph-cutの方法ではp=1に
近い方が経験的に良いので効率的な解法欲しい
– PCAで最大固有ベクトルをSparseにしたい
通常(p=2)どちらもIPM（逆べき乗法）を使用して行
列の固有値/固有ベクトルを用いる方法で解かれる．
1. 固有値問題自体を一回非線形(p>=1)に拡張する
2. IPMを非線形な場合の固有値問題に拡張
3. 拡張したIPMでこの２つの問題を解く
All proofs had to be omitted due to space restrictions and
can be found in the supplementary material.
2

3. ベキ乗法 (Power Method)
（半正定値）対称行列Aの最大固有値/ベクトル
xk+1 =Axk
を繰り返すと，xkは最大固有値に対応する固有
ベクトルの定数倍に近づく．理由：
3

4. Courant-Fischerの定理
(2)
レイリー商．
Courant-Fischerの
定理は，
固有値・固有ベクトル
をレイリー商との
関係から説明する
定理．
http://www.math.meiji.ac.jp/~mk/labo/text/generalized-eigenvalue-
problem/node16.html
4

5. レイリー商の非線形拡張
(2) (3)
関数R,Sに必要な条件を列挙してやる
A:対称n x n
f∈Rn
凸 (convex)
vが固有ベクトル
⇒α∈R, αvも
偶関数 (even)
固有ベクトル． p-homogeneous あるpに対して
S(f)=0 ⇔ f=0
Lipschitz連続 なら関数Gは
p-homogeneous.
微分不可能な点を含む場合が
あってもよい．
Lipschitz連続は微分不可能な点が
高々測度0であることに使われる．
（Rademacherの定理） 5

6. 固有値問題の非線形拡張
(2)
と，おく．
R,Sがquadratic functionなら，通常の(1)の場合に帰着．
簡単に確かめる：R(f)=<f,Bf>, S(f)=<f,Cf>
Bf – λCf = 0⇒Bf=λCf⇒A=C-1Bとおけば(1)
C-1が存在しない⇒f!=0かつ<f,Cf>=0であるようなfが存在する⇒S(f)=0⇔f=0に反す
Fが微分可能なら∇は普通の微分だと思って良い．
Fが微分不可能な点を含む場合，一般化微分を使う．
6

7. 一般化微分 (general differential)
Fがnonconvex, nondifferentialな場合に微分の
概念を拡張．
Fがconvexの時は，∂Fは劣微分，F0は方向微分
と一致．
7

8. Theorem 2.2
通常の線形代数の場合で考えると，
fがF=R(f)/S(f)のcritical point⇔∇F(f)=0
⇔∇(<f,Af>)-λ∇(<f,f>)=0, λ=R(f)/S(f)
⇔Af-λf=0, λ=<f,Af>/<f,f>
定義より，fはAの固有ベクトルで，λがAの固有値．
定理2.2は，一般の場合でも，⇔が⇒なら成り立つよ，さらにSが連続微分可能
なら，⇔が保たれるよ，と言っている．
8

9. ベキ乗法 (Power Method)
半正定値対称行列Aの最大固有値/ベクトル
xk+1 =Axk
を繰り返すと，xkは最大固有値に対応する固有
ベクトルの定数倍に近づく．理由：
9

10. Inverse Power Method
Inverse Power Method（逆べき乗法）：半正定値対称行列Aの最
小固有値に対応する固有ベクトルを求める方法．
を，fが収束するまで繰り返す．
つまり，各kで次の最適化問題を解くことに相当．
これを一般化すると，
10

11. Algorithm 1
そうしないと発散してしまう．
2-norm以外でもよい．
necessary to guarantee descent
11

12. inner optimization problem (p=1)
inner optimization problem
•s(fk)をどうやって見つける？
•早く解きたい．
1-Laplacianの場合は凸性は保たれる
ので普通に解いてもよいが，
双対問題を考えるともっと効率的．
p>1はこの論文では直接使わ sparse PCAの場合は，解析解で出る．
ないが，悔しいから書かれて
いるだけなので，省略．
12

13. 収束証明
更新すると必ず小さい固有値に近づき良くなりますよ．
Algorithm 1は，下の（５）式のλ*に近づきますよ．
13

14. Application2: sparse PCA
データ行列Xに対して，通常のPCAで第一主成分fを求めるとは：
これは，次の問題と同じ：
目的としては，f*をsparseにしたい．そのためには，1-normの項を導入して，
とし，これに対して，前述のIPMを適用すれば良い．
論文ではApplication 1（p-Laplacian)とApplication 2（PCA)の順だが，
Applicaiton2の方がstraight-forwardなので，
14

15. 再掲：Algorithm 1
inner optimization problem
15

16. Algorithm 4: Sparse PCA
4.でinner optimization problemが閉形式で解けるのがミソ
16

17. Application 1: p-Laplacian, Graph-
cut
いわゆる普通のGraph laplacian (2-Laplacian)
=1/2 fT (D-W) f
graph Laplacian
各エッジの重要度×(エッジの両端のノードのスコアの差)2
重要なエッジの両端のスコアは極端に違わないよう
にして欲しい．通常は，この問題のsecond
eigenvector (2番目に小さい固有値に対応する固有
ベクトル）を求め，fとする．（最小固有値=0だから）
p-Laplacian:
17

18. Cheeger cut
頂点集合がV，weight matrixがWであるようなグラフGの頂点を２つに分け
る．
とすると，h_RCCは次のように書けることが知られている．
1-Laplacian
18

19. 提案する問題
つまり，この問題の固有ベクトルはmedian zeroという特性をも
つ．一方，この問題のsecond eigenvectorはh_RCCに一致する
が，second eigenvectorを直接求めることは出来ない．
（線形じゃないからGram-Schmidtのようなことが出来ないため？
そこで， Algorithm 1でmedian zero という条件を満たしながら更
新していくアルゴリズムを提案し，収束を証明する．
19

20. 再掲：Algorithm 1
20

21. Algorithm 3
median 0 なので，medianの分を引く
vはs(f)に相当．medianを引いても
4.の目的関数の値が保たれるように
をみたすように更新
RCCに関して通常のp=2のLaplacianを使った方法より必ず良いことが証明
できる．
21

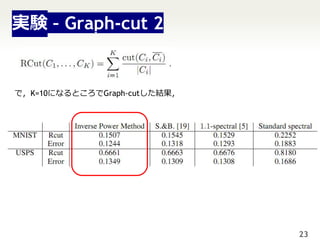
22. 実験 – Graph cut
two-moonsをどれだけ上手くGraph-cutで分けられるか．
1-Laplacian 2-Laplacian
2000点からなるtwo-moonsを100回描画したときの性能：
22

23. 実験 – Graph-cut 2
で，K=10になるところでGraph-cutした結果，
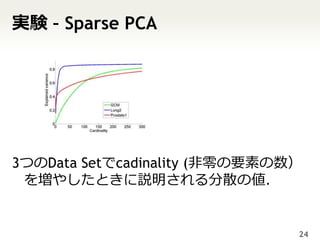
23

24. 実験 – Sparse PCA
3つのData Setでcadinality (非零の要素の数）
を増やしたときに説明される分散の値．
24

25. まとめ
やりたかったこと：
行列操作による典型的な２つの問題，Graph-cutと
PCAの第一主成分についてSparse（p=1に近い）解
を得たい．
前者はそうすると性能が上がることが経験的に知られてい
るから．後者は解釈しやすくなるから．
個々の問題でSparseにする方法は色々提案されてい
るが，元の固有値問題を一般化してp=1の場合を考
え，IPMも一般化すると両方の問題に対して収束性
が示された良いアルゴリズムが一気に得られるよ．
25

26. ご清澄ありがとうございました
26