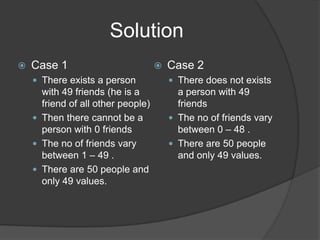
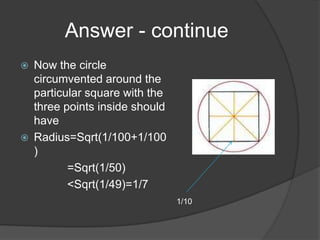
The document discusses the pigeonhole principle, which states that if n items are put into m containers where n > m, then at least one container must contain more than one item. It provides various formulations and applications of the principle in areas like data compression, hash tables, and the Chinese Remainder Theorem. The principle is believed to have first been stated by Dirichlet in 1834 and is also known as the drawer or shelf principle. Examples are given to illustrate how it can be used to solve problems related to birthdays, friend relationships, and geometry.

1. J.M.S.S. Silva

2. Pigeon-hole Principle
 If n (> m)
pigeons are put
into m
pigeonholes, th
ere's a hole
with more than
one pigeon.

3. Alternative Forms
• If n objects are to be allocated to m
containers, then at least one container
must hold at least ceil(n/m) objects.
• For any finite set A , there does not exist
a bijection between A and a proper
subset of A .
• Let |A| denote the number of elements in
a finite set A. For two finite sets A and
B, there exists a 1-1 correspondence
f: A->B iff |A| = |B|.

4. History
 The first statement of the
principle is believed to
have been made by
Dirichlet in 1834 under the
name Schubfachprinzip
("drawer principle" or
"shelf principle")
 Also known as Dirichlet's
box (or drawer) principle

5. General Problems
 There 750 students in the a batch at
UOM. Prove that at least 3 of them have
their birthdays on the same date ?
○ 366 * 2= 732 < 750
○ Thus at least 3 students have the birthday
on the same date.

6. Problems on Relations
 There are 50 people in a room. some of them are
friends. If A is a friend of B then B is also a friend of
A. Prove that there are two persons in the room
who have a same number of friends.
 In league T20 tournament of 16 cricket
teams, every two teams have to meet in a game.
Prove that at any time there are two teams which
played equal number of matches.

7. Solution
 Case 1  Case 2
 There exists a person  There does not exists
with 49 friends (he is a a person with 49
friend of all other people) friends
 Then there cannot be a  The no of friends vary
person with 0 friends between 0 – 48 .
 The no of friends vary  There are 50 people
between 1 – 49 . and only 49 values.
 There are 50 people and
only 49 values.

8. Problems On Divisibility
 Prove that there
exists a multiple of
2009 whose decimal
expansion contains
only digits 1 and 0.

9. Answer
 Consider 2010 numbers
- 1,11,111,1111, … ,1111…111.
 Each of these numbers produce one of 2009
remainders
- 0,1,2,3 ,…,2008
 We have 2010 numbers and 2009 remainders
 By pigeon-hole principle some two numbers have the
same remainder .Let those 2 numbers be A and B
(A>B)
 Consider A-B. which is a multiple of 2009.
- In the form of 11…1100…000

10. Problems On Divisibility
 Prove that of any 52 natural numbers one can find
two numbers n and m such that either their sum m+n
or difference m-n is divisible by 100.
 Consider sets {0},{1,99},{2,98}….{49,51},{50}
 There are 51 sets
 By pigeon hole principle at least 1 set should have 2
members
 If we consider any set above if they have 2 members in the
set, m+n or m-n is divisible by 100

11. Problems on Geometry
 51 points are placed, in a random way, into a
square of side 1 unit. Can we prove that 3 of these
points can be covered by a circle of radius 1/7 units
?

12. Answer
 To prove the result, we may divide
the square into 25 equal smaller
squares of side 1/5 units each.
Then by the Pigeonhole Principle, at
least one of these small squares
should contain at least 3 points.
Otherwise, each of the small
squares will contain 2 or less points
which will then mean that the total
number of points will be less than
50 , which is a contradiction to the
fact that we have 51 points in the
first case !

13. Answer - continue
 Now the circle
circumvented around the
particular square with the
three points inside should
have
 Radius=Sqrt(1/100+1/100
)
=Sqrt(1/50)
<Sqrt(1/49)=1/7
1/10

14. Applications
 Lossless data compression cannot guarantee
compression for all data input files.
 The pigeonhole principle often arises in
computer science. For example, collisions are
inevitable in a hash table because the number
of possible keys exceeds the number of
indices in the array
 In probability theory, the birthday problem, or
birthday paradox pertains to the probability
that in a set of randomly chosen people some
pair of them will have the same birthday

15. Applications
 The proof of Chinese Remainder Theorem
is based on pigeon-hole principle
Let m and n be relatively prime positive
Integers. Then the system:
x = a (mod m)
x = b (mod n)
has a solution.

16. References
 http://en.wikipedia.org/wiki/Pigeonhole_principle
 http://en.wikipedia.org/wiki/Johann_Peter_Gustav_
Lejeune_Dirichlet
 http://en.wikipedia.org/wiki/Lossless_data_compre
ssion#Limitations
 Article on "What is Pigeonhole Principle?" by
Alexandre V. Borovik, Elena V. Bessonova.
 Article on "Applications of the Pigeonhole
Principle" by Edwin Kwek Swee Hee ,Huang
Meiizhuo ,Koh Chan Swee ,Heng Wee Kuan
, River Valley High School

17. Thank You