Physics of tablet compression

Amity Institute of Pharmacy
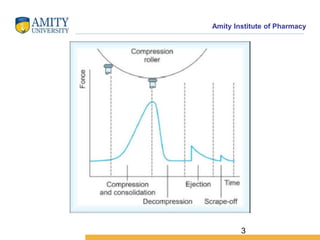
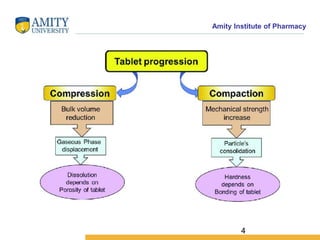
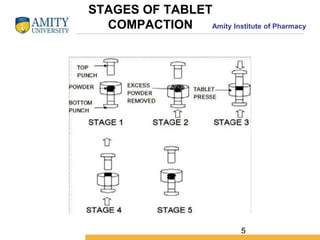
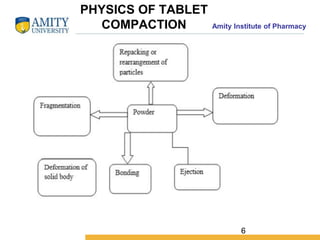
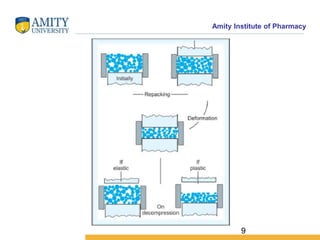
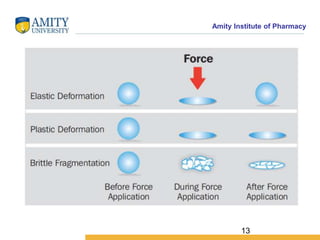
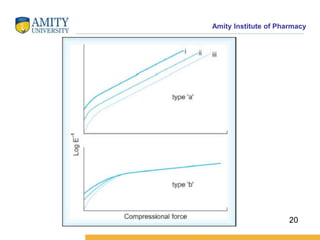
PHYSICS OF TABLET
COMPRESSION AND
COMPACTION
UNNATI GARG
M. Pharm (Pharmaceutics)
1

INTRODUCTION
COMPACTION:
Compaction of a powder is a general term used to describe
a situation in which powdered material is subjected to some
level of mechanical force.
COMPRESSION:
Compression of a powder means reduction in the bulk
volume of a material as a result of displacement of the
gaseous phase under pressure.
2

STAGES OF TABLET
COMPACTION
5

PHYSICS OF TABLET
COMPACTION
6

PARTICLE
REARRANGEMENT
• Particles rearranged under low pressure to form a closer
packing structure
• The finer particles enter the voids
• Energy evolved
7

DEFORMATION
• Depends on physical properties of the material as well
as the amount of compaction force applied.
• Energy lost during this process
• As the load increases, however, rearrangement
becomes more difficult, and further compression involves
some type of particle deformation
• Deformation can be of three types:
a. Elastic Deformation
b. Plastic Deformation
c. Brittle fracture
8

Elastic Deformation:
• If on removal of the load, the deformation is to a large extent
spontaneously reversible, i.e. if it behaves like rubber, then the
deformation is said to be elastic.
• With several pharmaceutical materials, such as acetylsalicyclic
acid and microcrystalline cellulose, elastic deformation
becomes the dominant mechanism of compression within the
range of maximum forces normally encountered in practice.
10

Plastic Deformation:
• In other groups of powdered solids, an elastic limit, or yield
point, is reached, and loads above this level result in
deformation not immediately reversible on removal of the
applied force.
• Bulk volume reduction in these cases results from plastic
deformation and/or viscous flow of the particles, which are
squeezed into the remaining void spaces, resembling the
behavior of modeling clay. This mechanism predominates in
materials in which the shear strength is less than the tensile or
breaking strength.
11

Brittle Fracture:
• When the shear strength is greater, particles may be
preferentially fractured, and the smaller fragments then help to
fill up any adjacent air space. This is most likely to occur with
hard, brittle particles and in fact is known as brittle fracture;
sucrose behaves in this manner.
• The predisposition of a material to deform in a particular
manner depends on the lattice structure, in particular whether
weakly bonded lattice planes are inherently present.
12

13

BONDING OF
PARTICLES
• Interparticulate bonds are formed and frictional heat is
generated.
• The mechanical strength of a tablet depends on the
dominating bonding mechanism between the particles and
the surface area over which these bonds act.
• When the surfaces of two particles approach each other
closely enough, their surface energies result in a strong
attractive force, a process called cold welding.
1
4

EJECTION
• This process requires force in three phases
• The force necessary to eject a tablet involves the
distinctive peak force required to initiate ejection, by
breaking of die wall– tablet adhesion.
• The second stage involves the force required to push the
tablet up the die wall,
• The final stage is marked by a declining force of ejection
as the tablet emerges from the die.
15

FORCE
DISTRIBUTION
Most investigations of the fundamentals of tabletting have been
carried out on singlestation presses (sometimes called eccentric
presses), or even on isolated punch and die sets in conjunction
with a hydraulic press.
Most systems work with force being applied to the top of a
cylindric powder mass. This simple compaction system provides
a convenient way to examine the process in greater detail. More
specifically, the following basic relationships apply. Since there
must be an axial (vertical) balance of forces:
FA = FL + FD
FA: force applied to upper punch,
FL- force transmitted to lower punch,
FD- reaction at die wall
16

Because of this inherent difference between the force applied at
the upper punch and that affecting material close to the lower
punch, a mean compaction force, FM, has been proposed, where:
FM = (FA + FL) /2
A recent report confirms that FM offers a practical friction-
independent measure of compaction load, which is generally
more relevant than FA. In single-station presses, where the
applied force transmission decays exponentially. A more
appropriate geometric mean force (FG) might be:
FG = (FA x FL) 1/2
17

COMPACTION
EQUATION
HECKEL EQUATION
The Heckel equation is based on the assumption that
densification of the bulk powder under force follows first-order
kinetics. It is expressed as:
where, Ky is a material-dependent constant inversely proportional
to its yield strength S (Ky = 1/3S), and KR is related to the initial
repacking stage, and hence E0, P is applied pressure and E is
porosity.
18
𝒍𝒐𝒈 𝟏
𝑬 = 𝒌𝒚𝑷 + 𝒌𝑹

• The particular value of Heckel plots arises from their ability to
identify the predominant form of deformation in a given
sample. Materials that are comparatively soft and that readily
undergo plastic deformation retain different degrees of
porosity, depending upon the initial packing in the die.
• This in turn is influenced by the size distribution, shape, etc. of
the original particles. Heckel plots for such materials are
shown by type ‘a’; sodium chloride is a typical example.
• Conversely, harder materials with higher yield pressure values
usually undergo compression by fragmentation first, to provide
a denser packing. Label ‘b’ shows Heckel plots for different
size fractions of the same material that are typical of this
behavior. Lactose is one such material.
19

20

• The two regions of the Heckel plot are thought to represent the
initial repacking stage and the subsequent deformation
process, the point of intersection corresponding to the lowest
force at which a coherent tablet is formed.
• In addition, the crushing strength of tablets can be correlated
with the value of Ky of the Heckel plot; larger values of Ky
usually indicate harder tablets. Such information can be used
as a means of binder selection when designing tablet
formulations.
21

REFERNCES
• Khar, Roop K; Vyas, SP; Ahmad, Farhan J; Jain, Gaurav K.
Industrial Pharmacy (pp. 1203-1204). CBS Publishers &
Distributors Pvt Ltd, India.
• Patel S, Kaushal AM, Bansal AK. Compression physics in the
formulation development of tablets. Crit Rev The Drug Carrier
Syst. 2006;23(1):1-65. doi:
10.1615/critrevtherdrugcarriersyst.v23.i1.10. PMID: 16749898
• Yadav P., Sahdev A.K., Physics of tablet with compaction and
compression process for novel drug dosage form, International
Journal of Advanced Science and Research; July 208, 4(3); 28-
34
22

23

Physics of tablet compression

More Related Content

What's hot

Similar to Physics of tablet compression

More from Unnati Garg

Recently uploaded

Physics of tablet compression