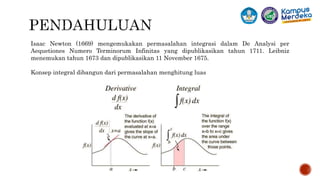
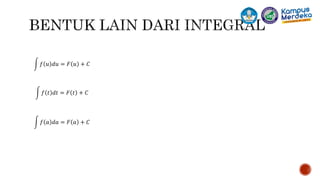
Mata kuliah ini membahas konsep integral tak tentu, tertentu, dan operasi matriks untuk memecahkan permasalahan teknik. Mahasiswa akan mempelajari teknik-teknik integral seperti integral dasar, integral pecah rasional, dan integral parsial beserta penerapannya dalam masalah teknik sipil menggunakan integral. Penilaian terdiri atas tugas, UTS, dan UAS. Kuliah dilaksanakan secara tatap muka atau daring tergantung kebijakan univers

1. Aswar Amiruddin, ST., MT

2. Nama mata kuliah : Matematika Teknik 1
Kode mata kuliah : TW123112
SKS : 3 SKS
Capaian pembelajaran MK :
Memahami konsep integral tak tentu, tertentu dan operasi matriks serta
memecahkan permasalahan menggunakan konsep integral dan juga
matriks.
Referensi :
Erwyn, K. Matematika Teknik Lanjutan. 1993. Erlangga. Jakarta
Varberg, Purcell, Rigdon. Kalkulus. 2007. Erlangga. Jakarta.
Ratnadewi, dkk. Matematika Teknik Untuk Perguruan Tinggi. 2016.
Rekayasa Sains
KA. Stroud. Matematika Teknik.
2

3.  Integral dasar
 Integral pecah rasional
 Integral parsial
 Integral lipat dua, integral lipat tiga
 Penyelesaian masalah ketekniksipilan dengan integral
 PTS
3

4. a. Tugas 30%
b. PTS 30%
c. PAS 40%
d. Metode perkuliahan : Tatap muka / Hybrid
(bergantung pada kebijakan Pimpinan)
e. Platform kuliah daring : Borneo E learning,
Zoom

5. Silahkan klik berikut untuk mengetahui pemahaman integral mahasiswa
Link :

6. Isaac Newton (1669) mengemukakan permasalahan integrasi dalam De Analysi per
Aequetiones Numero Terminorum Infinitas yang dipublikasikan tahun 1711. Leibniz
menemukan tahun 1673 dan dipublikasikan 11 November 1675.
Konsep integral dibangun dari permasalahan menghitung luas

7. Setiap operasi di matematika memiliki kebalikan,
+ − ÷ ×
Sementara itu integral merupakan kebalikan dari turunan, integral merupakan
antiturunan
𝑓(𝑥) 𝑓′(𝑥)
turunan
integral

8. Misal F(x) merupakan antiturunan dari f(x)
adalah lambang integrasi, f(x) dinamakan integran, dan C konstanta integral
𝑓(𝑥) 𝑑𝑥 = 𝐹 𝑥 + 𝐶
Misal fungsi 𝑥2 jika diturunkan menjadi 2x, mengacu pada definisi integral pada slide
7 maka integral dari 2x adalah 𝑥2 atau dalam matematika dapat dituliskan :
2𝑥 𝑑𝑥 = 𝑥2 + 𝐶

9. Jika 𝑓 𝑥 = 𝑥2
+ 1, maka 𝑓′
𝑥 = 2𝑥
Jika 𝑓 𝑥 = 𝑥2 + 2, maka 𝑓′ 𝑥 = 2𝑥
Jika 𝑓 𝑥 = 𝑥2
+ 3, maka 𝑓′
𝑥 = 2𝑥
Jika 𝑓 𝑥 = 𝑥2 + 𝐶, maka 𝑓′ 𝑥 = 2𝑥
Misal dari beberapa fungsi berikut
Berdasarkan contoh di atas dapat disimpulkan jika 𝑓′
𝑥 = 2𝑥, maka integral 𝐹 𝑥 = 𝑥2
+ 𝐶

10. Dari uraian sebelumnya nampak bahwa jika 𝑓′
𝑥 = 𝑥𝑛
, maka 𝑓 𝑥 =
1
𝑛+1
𝑥𝑛+1
+ 𝐶 atau
dapat dituliskan :
𝑥𝑛 𝑑𝑥 =
1
𝑛+1
𝑥𝑛+1 + 𝐶
𝑑𝑥 = 𝑥 + 𝐶
𝐾𝑓(𝑥) 𝑑𝑥 = 𝐾 𝑓(𝑥) 𝑑𝑥
𝑓 𝑥 ± 𝑔 𝑥 𝑑𝑥 = 𝑓 𝑥 𝑑𝑥 ± 𝑔 𝑥 𝑑𝑥
Rumus dasar integral tak tentu

11. Latihan soal :
1. 5 𝑑𝑥
2. 𝑥3
𝑑𝑥
3. 𝑥 𝑥 𝑑𝑥
4. 6𝑥2 + 8𝑥 𝑑𝑥
5. 2𝑥 − 6 𝑑𝑥

12. 𝑓 𝑢 𝑑𝑢 = 𝐹 𝑢 + 𝐶
𝑓 𝑡 𝑑𝑡 = 𝐹 𝑡 + 𝐶
𝑓 𝑎 𝑑𝑎 = 𝐹 𝑎 + 𝐶

14. Integrasi u-substitusi merupakan teknik yang paling mudah dalam menyelesaikan
persoalan integral. Kita memilih fungsi permisalan u dari sebuah integran. Jika fungsi u
sudah dipilih, selanjutnya semua unsur yang mengandung nilai x kita gantikan dengan
nilai u. Langkah-Langkah penyelesaian teknik integrasi u-substitusi adalah:
a. Pilih fungsi yang diganti, misalkan u = g(x)
b. Hitung du/dx = g’(x)
c. Buat substitusi u = g(x) dan du = g’(x)dx
d. Evaluasi proses integrasi
e. Gantikan u oleh g(x) untuk jawaban akhir dalam x.
Catatan:
Setiap jawaban dari hasil integral (fungsi primitif)  shg turunannya sama dengan
integran

16. (𝑥3 + 2)23𝑥2𝑑𝑥 = ⋯
sin 5𝑥 𝑑𝑥 = ⋯

17. Teknik integrasi bagian/parsial umumnya dilakukan jika kita menjumpai integran terdiri
dari dua fungsi yang berbeda. Untuk integran yang terdiri dari dua buah fungsi, ada
bagian integran yang dimisalkan sebagai fungsi u=g(x) dan unsur yang lain dimisalkan
sebagai dv. Rumus umum untuk menyelesaikan soal integrasi bagian adalah:
Catatan:
Setiap jawaban dari hasil integral (fungsi primitif)  shg turunannya sama dengan
integran

18. 𝑥 𝑒𝑥𝑑𝑥 = ⋯
𝑥 sin 𝑥 𝑑𝑥 = ⋯
𝑥2 𝑒𝑥𝑑𝑥 = ⋯

20. Berpikir adalah pekerjaan berat, yang mungkin
menjadi alasan mengapa begitu sedikit yang terlibat
di dalamnya.