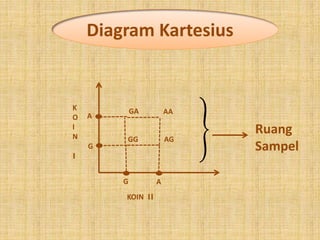
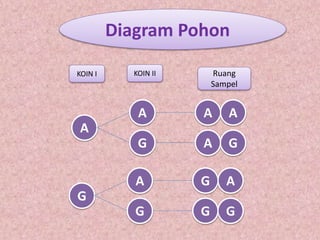
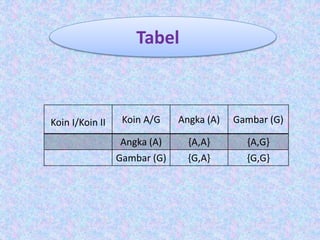
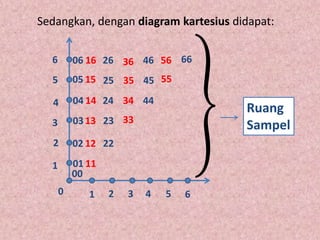
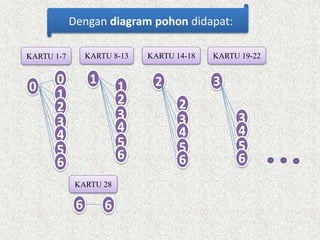
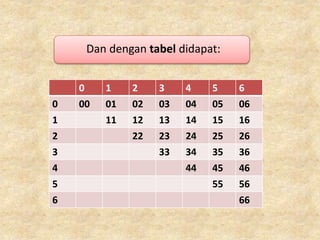
Dokumen ini membahas tentang pengertian ruang sampel dan cara menemukan peluang empirik dengan menggunakan berbagai metode, termasuk percobaan pelemparan koin dan dadu. Juga dijelaskan tentang cara penyajian ruang sampel menggunakan daftar, diagram kartesian, diagram pohon, dan tabel. Contoh dilengkapi dengan analisis jumlah kemungkinan hasil pada percobaan yang dilakukan.

1. DINI NURFADILAH EHOM
1101874
PENDIDIKAN MATEMATIKA
UNIVERSITAS PENDIDIKAN INDONESIA

2. KOMPETENSI DASAR
INDIKATOR
10.1 MENEMUKAN
KONSEP RUANG SAMPEL

3. KOMPETENSI DASAR
Menemukan peluang empirik dari data luaran
(output) yang mungkin diperoleh berdasarkan
sekelompok data.
Melakukan percobaan untuk menemukan
peluang empirik dari masalah nyata serta
menyajikannya dalam bentuk tabel dan grafik.

4. INDIKATOR
 Menyajikan ruang dan titik sampel dengan
cara mendaftar
 Menyajikan ruang dan titik sampel dengan
diagram kartesisus
 Menyajikan ruang dan titik sampel dengan
diagram pohon
 Menyajikan ruang dan titik sampel dengan
tabel

5. ILUSTRASI 1
Bila yang muncul angka, maka salah satu tim diminta
Wasit memanggil kapten kedua tim dan meminta keduanya
Sebelum pertandingan sepak bola dimulai, wasit melambungkan
menentukan tempat atau menendang duluan sesuai perjanjian
koin untuk menentukan posisi awal masing-masing tim pemain.
untuk memilih angka atau gambar.
awal yang disepakati.

6. 10.1 MENEMUKAN KONSEP RUANG SAMPEL
Cara pengundian dengan menggunakan koin seperti pada
ilustrasi tersebut merupakan salah satu contoh percobaan
statistika.
Hasil percobaan pada pelemparan koin yang dapat terjadi
adalah munculnya angka (A) atau gambar (G).
Peristiwa munculnya angka (A) atau gambar (G) pada
pelemparan sebuah koin disebut kejadian tunggal.
Apabila semua hasil percobaan tersebut dihimpun dalam
suatu himpunan S, dengan S = { A, G}, maka:
S disebut ruang sampel
A dan G disebut titik sampel
Banyak anggota S dinyatakan dengan n(S)

7. Jadi, pada pelemparan sebuah
koin, didapat ruang sampel S
dengan S = {A, G} dan n(S)=2.
Sekarang, tentukan ada berapa
banyak titik sampel yang
didapat pada pelemparan
sebuah dadu?

8. Sebuah dadu memiliki mata di setiap sisinya.
Jumlah mata pada setiap sisi dimulai dari 1
sampai 6. Maka, semua kemungkinan yang akan
muncul dari kejadian tersebut adalah:
Bagaimana dengan pelemparan
dua buah dadu? Apakah akan
didapat n(S) yang sama dengan
pelemparan 1 buah dadu saja?
1 2 3 4 5 6
Jadi, pada pelemparan sebuah dadu didapat
sebuah ruang sampel S dengan:
S = {1, 2, 3, 4, 5, 6} dan n(S) =
6

9. ILUSTRASI 2
Suatu hari, Sita, Dewi, Nana dan Gigin
bermain MONOPOLI. Mereka mengocok
2 dadu sekaligus secara bergiliran
Jadi, ada berapa pasang mata dadu
yang DGNeSiawgintiinaammmeneenndddaapaappaataattmmmaataaatttaadddaadaadduuu4265---mungkin muncul pada setiap
4636
pengocokan?

10. Peristiwa pengundian dua buah dadu seperti pada
ilustrasi tersebut adalah kejadian majemuk, karena
terdiri lebih dari 1 kejadian yang akan muncul.
Pada setiap kali pengundian akan muncul 2 mata dadu
sekaligus yaitu:
1,1 1,2 1,3 1,4 1,5 1,6
2,1
2,2 2,3 2,4 2,5 2,6
3,1
3,2 3,3 3,4 3,5 3,6
4,1
4,2 4,3 4,4 4,5 4,6
5,1
5,2 5,3 5,4 5,5 5,6
6,1
6,2 6,3 6,4 6,5 6,6

11. Jadi, pada pelemparan 2 buah dadu didapat sebuah
ruang sampel S dengan :
S = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2),
(2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5),
(3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2),
(5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5),
(6,6)} dan n(S) = 36
Sekarang, tentukan ada berapa banyak
anggota ruang sampel yang didapat pada
pelemparan 2 buah koin secara bersamaan?

12. Sebuah koin memiliki sisi angka (A)
dan gambar (G)
Pada setiap pelemparan akan
menghasilkan pasangan :
A A
G A
A G
G G
Jadi, pada pelemparan 2 buah koin didapat
sebuah ruang sampel S dengan S = {(AA), (AG),
(GA), (GG)} dan n(S) = 4

13. Adakah cara lain?
Cara yang sejak tadi kita gunakan
dalam menentukan titik-titik
sampel pada suatu percobaan
disebut dengan cara mendaftar.

14. • Diagram Cartesius
• Diagram Pohon
• Tabel
Ada 3 cara lain yang dapat digunakan
untuk menyajikan semua kejadian yang
muncul pada percobaan statistika

15. Diagram Kartesius
K
O
I
N
I
GG
KOIN II
A
A
G
G
GA
AA
AG
Ruang
Sampel

16. Diagram Pohon
KOIN I KOIN II Ruang
Sampel
A
A
G
A
A
G
A
G
A
G
G
A
G
G

17. Tabel
Koin I/Koin II Koin A/G Angka (A) Gambar (G)
Angka (A) {A,A} {A,G}
Gambar (G) {G,A} {G,G}

18. Nah sekarang, sajikanlah ruang dan titik sampel pada
pencabutan satu set kartu domino dengan cara:
a. Mendaftar
b. Diagram Kartesius
c. Diagram Pohon
d. Tabel
TUGAS
----- Selamat Mengerjakan -----

19. Jadi, dengan cara mendaftar didapat:
Kartu ke 1 muncul 00
Kartu ke 2 muncul 01
Kartu ke 3 muncul 02
Jawab :
Setiap kartu domino memiliki dua
mata pada setiap lembarnya. Paling
sedikit .
mata nol dan paling banyak
mata .
enam.
.
Misalkan Kartu ke 28 kartu muncul bermata 66
satu-satu
ditulis Sehingga 11,
diperoleh:
tiga-tiga ditulis 33,
dan seterusnya.
Pada kartu domino, 23 sama dengan 32, artinya
tidak ada pasangan yang berulang.
S = {(00) (01), (02), (03), (04), (05), (06), (11), (12),
(13), (14), (15), (16), (22), (23), (24), (25), (26), (33),
(34), (35), (36), (44), (45), (46), (55), (56), (6,6)} dan
n(S) = 28

20. Sedangkan, dengan diagram kartesius didapat:
16
15
14
13
12
26
25
24
23
36
35
34
46
45
56 66
1 2 3 4 5 6
6
5
4
3
2
1
0
Ruang
Sampel
06
05
04
03
02
01
00
11
22
33
44
55

21. Dengan diagram pohon didapat:
KARTU 1-7 KARTU 8-13 KARTU 14-18 KARTU 19-22
0
0
12
34
56
1
6 6
1234
56
2
2
34
56
3
34
56
KARTU 28

22. Dan dengan tabel didapat:
0 1 2 3 4 5 6
0 00 01 02 03 04 05 06
1 11 12 13 14 15 16
2 22 23 24 25 26
3 33 34 35 36
4 44 45 46
5 55 56
6 66

23. SEKIAN
DAN
TERIMA KASIH