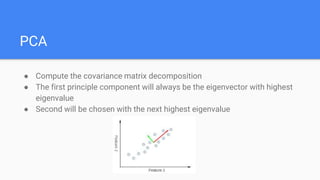
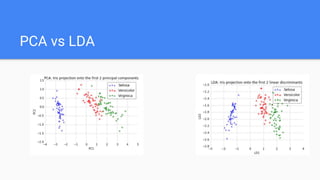
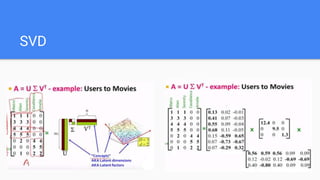
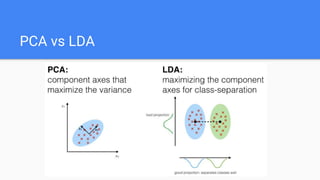
The document provides an overview of dimensionality reduction techniques, including PCA, SVD, and LDA. PCA uses linear projections to reduce dimensions while preserving variance in the data. It computes eigenvectors of the covariance matrix. SVD is similar to PCA but works directly with the data matrix rather than the covariance matrix. LDA aims to maximize class separability during dimensionality reduction for classification tasks. It computes within-class and between-class scatter matrices. While PCA maximizes variance, LDA maximizes class discrimination.

1. zekeLabs
Dimensionality Reduction

2. “Goal - Become a Data Scientist”
“A Dream becomes a Goal when action is taken towards its achievement” - Bo Bennett
“The Plan”
“A Goal without a Plan is just a wish”

3. ● Real Data
● PCA
● Eigenvectors
● Covariance Matrix
● Matrix Decomposition
● Covariance Matrix Decomposition
● SVD
● PCA vs SVD
● LDA
● PCA vs LDA
Overview of
Dimensionality
Reduction
Techniques

4. Real Data
● Real world data and information therein may be
○ Noisy
■ Some dimensions may not carry any useful information
■ Variation in that dimension is purely due to noise in the observations
○ Redundant
■ One variables may carry the same information as the other variable
■ Information covered by a set of variable may overlap
● How to reduce the dimensions?

5. PCA
● Dimensionality reduction technique
● Linear projection of Data into Orthogonal Basis System
● Minimum redundancy and preserves variance in the data
● Smallest reconstruction error
● Applications include Image-compression, Data Visualisation

6. Eigenvectors
● If A is a square matrix, vector v is an eigenvector of if there is a scalar 𝝀
such that
Av = 𝝀v
● Example:
● Simply, if we transform the eigenvector, it doesn’t change it’s direction
● Matrix multiplication of A with v is a transformation

7. Covariance Matrix
● Covariance Matrix of X
● Diagonal Terms: Variance
● Off-Diagonal Terms: covariance
● Covariance matrix is always symmetric
● n - no. of observation in X here

8. Matrix Decomposition
● If square d x d matrix S is a real and symmetric matrix then

9. Covariance Matrix Decomposition
● If square d x d matrix S is a real and symmetric matrix then

10. PCA
● Compute the covariance matrix decomposition
● The first principle component will always be the eigenvector with highest
eigenvalue
● Second will be chosen with the next highest eigenvalue

11. Linear Discriminant Analysis - LDA
● Dimensionality reduction technique in the pre-processing step for pattern-
classification and machine learning applications.
● Project data into lower dimension with good class separability to avoid
over-fitting & reduced computation
● In addition to finding component axis that maximizes the variance of our
data, we are additionally interested in the axes that maximize the
separation between multiple classes
● project a feature space onto a smaller subspace k (where k≤n−1) while
maintaining the class-discriminatory information.

12. PCA vs LDA
● It’s not true that LDA is superior
than PCA for classification
● PCA outperforms classification
for smaller dataset.
● PCA & SVD can be combined

13. PCA vs LDA

14. Normality Assumptions of LDA
● It should be mentioned that LDA assumes normal distributed data,
features that are statistically independent, and identical covariance
matrices for every class.
● However, this only applies for LDA as classifier and LDA for dimensionality
reduction can also work reasonably well if those assumptions are violated.

15. Singular Value Decomposition - SVD

16. SVD - Basics

17. SVD

18. SVD - Understanding Decomposition

19. SVD - Understanding Decomposition

20. PCA vs SVD
● The eigenvectors of C are the same as the right singular vectors of X
● The eigenvectors of covariance matrix are same as vector V
● Working directly with X will produce much more accurate results
● Working directly with X is faster

21. LDA
● LDA - Linear Discriminant Analysis
○ Compute the d-dimensional mean vectors for the different classes from the dataset
○ Compute the scatter matrices (in-between-class and within-class scatter matrix)
○ Compute the eigenvectors and corresponding eigenvalues for the scatter matrices
○ Sort the eigenvectors by decreasing eigenvalues and choose kk eigenvectors

22. PCA vs LDA