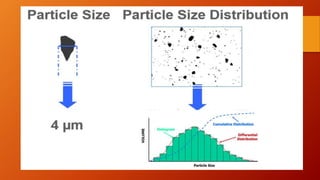
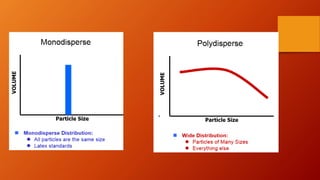
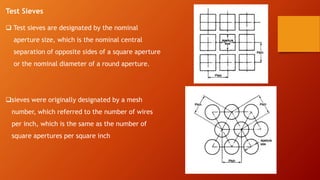
This document discusses particle size distribution (PSD), which is a list or function that defines the relative amounts of particles sorted by size. It explains that PSD is important for industries like pharmaceutical, chemical, ceramics, etc. It describes different size terminology used like micrometers and nanometers. It also discusses different ways to measure particle size based on volume, weight or area. Finally, it provides examples of analytical distribution functions used to model PSD like normal, log-normal and Weibull distributions.

1. Particle Size Distribution Function
By- Rohit Dixit

2. Objectives
Significance of Particle Size Distribution
Understanding of Particle Size and Particle Shape
 Particle Size Distribution (PSD)
 Particle Size Distribution: Measurement Techniques
Analytical distribution function

3. Who cares about particle size?
• Pharmaceutical
• Chemical
• Ceramics
• Cement
• Food
• Abrasives
• Cosmetics
• Mining
• Powder metals
• University
• Others

4. Size terminology
• The most common designation is micrometer or micron.
• For very small size nanometer is used.

6. Which is the most meaningful size?
Different size definition Different result

7. The Basic
• What size can be measured?

8. Which size to measure?
• Vol. based particle size equals the diameter of the sphere that has a same vol as the
given particle.
D=2*(3
3𝑉/4π)
Weight based particle size equals the diameter of the sphere that has a same weight
as the given particle.
D=2*(3
3𝑊/4π𝑑 𝑔)
Area based particle size equals the diameter of the sphere that has a same weight as
the given particle.
D=2(2
𝐴/4𝜋)

9. Particle Size Distribution
“Particle size distribution (PSD) of a powder, or
granular material, or particles dispersed in fluid,
is a list of values or a mathematical function
that defines the relative amounts of particles
present, sorted according to size.”

12. Symmetric and Asymmetric distribution
Distribution is along side of the center value Distribution is not same along side of the center value
Mean: Sum of values of a data set divided by number of values
Mode: most frequent set in data set
Median: Middle value separating the greater and lesser halves of a data set

13. Analytical distribution function
Some analytical distribution funtions are:
• Normal distribution
• Log-normal distribution
• Weibull distribution

14. Normal distribution
• Probability distribution function:
Where
µ is mean
σ is standard deviation
σ2 is variance

15. Log- normal distribution function:
Probability distribution function:
Where
µ is mean
σ is standard deviation
σ2 is variance

16. Weibull distribution
Probability distribution function:
Where
µ is mean
σ is standard deviation
σ2 is variance

17. Class example
Mean size: 135.9992 nm
Standard deviation :
37.38654

18. Normal distribution fitting
R^2 : .604

19. Thanks