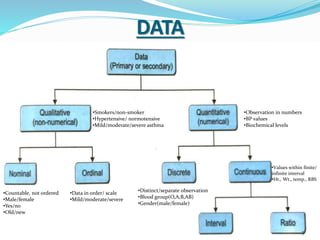
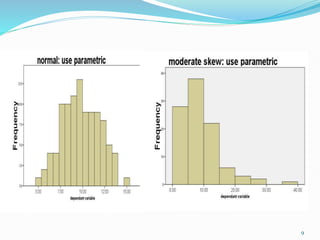
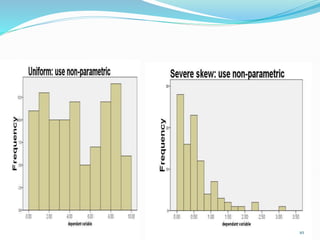
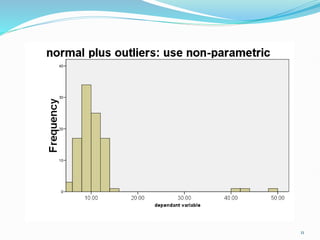
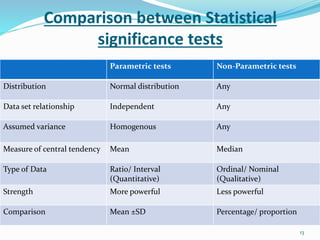
This document discusses statistical tests and data analysis. It defines statistical power and describes two broad classifications of data: qualitative and quantitative. It then discusses different measures of central tendency like mean, median and mode. The document outlines different types of data distribution such as normal, binomial and Poisson distributions. It compares parametric and non-parametric statistical tests and their strengths. Finally, it discusses some commonly used parametric tests like t-tests and ANOVA to compare means between two or more samples.

1. Dr. Devesh Pandey
MBBS, MD (Pharmacology)
8-12-2020 1

2. Statistical Tests
 Mathematical calculation or analysis of observed and
collected data from the population or sampling.
 Statistical Power- Result obtained of tests, measure of
probability that a statistical test rejects a false null
hypothesis or probability of finding a significant result.
 Broadly, data classified into two-
1. Qualitative data (non-numerical)
2. Quantitative data (numerical)
2

3. DATA
•Smokers/non-smoker
•Hypertensive/ normotensive
•Mild/moderate/severe asthma
•Observation in numbers
•BP values
•Biochemical levels
•Countable, not ordered
•Male/female
•Yes/no
•Old/new
•Data in order/ scale
•Mild/moderate/severe
•Distinct/separate observation
•Blood group(O,A,B,AB)
•Gender(male/female)
•Values within finite/
infinite interval
•Ht., Wt., temp., RBS
3

4. Measure of Data
(A) Mean-
 Arithmetic average of any given data.
(B) Median-
 Middle value of any given data when it is arranged in
ascending/ descending order.
(C) Mode-
 Very frequently occuring event in given data.
4

5. TYPES OF DATA DISTRIBUTION
(A) NORMAL (Gussian) DISTRIBUTION-
 Mean=Median=Mode
 Variables have tendency to cluster around central value with a
symmetric distribution on either side.
 Skew is zero
If tail skew towards right side- Positive skewed
If tail skew towards left side- Negative skewed
In skewed distribution Median- good measure of central
tendency.
• Such made to normal distribution by suitable transformation
by taking logarithum, square root or reciprocal.
5

6. 6

7. (B) BINOMIAL DISTRIBUTION-
 Data where only two possibilities.
 E.g. smokers/ non-smokers, male/ females, survived/
not survived.
 Two peaks
7

8. (C) POISSON DISTRIBUTION-
 Commonly used distribution in health sciences.
 Distribution of number of occurrences of some random
event in an interval of time or space.
8

9. 9

10. 10

11. 11

12. Classification
12

13. Comparison between Statistical
significance tests
Parametric tests Non-Parametric tests
Distribution Normal distribution Any
Data set relationship Independent Any
Assumed variance Homogenous Any
Measure of central tendency Mean Median
Type of Data Ratio/ Interval
(Quantitative)
Ordinal/ Nominal
(Qualitative)
Strength More powerful Less powerful
Comparison Mean ±SD Percentage/ proportion
13

14. Equivalent Tests
Parametric tests Non-Parametric tests
Correlation test- Pearson Spearman rank order
(Independent measures 2 groups)
Unpaired student t-test
Mann-Whitney U test
(Repeated measures 2 condition)
Paired t - test
Wilcoxon signed rank test
(Independent measures >2 conditions)
ANOVA one way
Kruskal-wallis test
(Repeated measures > 2 conditions)
ANOVA one way
Friedman test
14

15. PARAMETRIC TESTS
Parameter: is any numerical quantity that characterizes a
given population or some aspect of it.
P-value- (Statistical significance)
Represents risk observed in experiment due to chance.
Determines significance/non-significance of a result.
<0.05 value- significant (uncertainty of 5%)
Confidence interval (CI)- (Clinical significance)
95%- means 95% chance of cases to fall in the range.
15

16. Differences Between Means –
Parametric Data
t-Tests- compare the means of two parametric samples
 Excel: t-Test (paired and unpaired) – in Tools – Data
Analysis
 E.g. Is there a difference in the mean height of men and
women?
 E.g. A researcher compared the height of plants grown in
high and low light levels. Use a T-test to determine whether
there is a statistically significant difference in the heights of
the two groups
 E.g. the length and weight of something –> parametric vs.
did the bacteria grow or not grow –> non-parametric
16

17. ANOVA (Analysis of Variance)- compares the means of
two or more parametric samples.
 Excel: ANOVA – check type under Tools – Data Analysis
 E.g. Is there a difference in the mean height of plants grown
under red, green and blue light?
 E.g. A researcher fed pigs on four different foods. At the end
of a month feeding, he weighed the pigs. Use an ANOVA
test to determine if the different foods resulted in
differences in growth of the pigs.
17

18. Advantages of non-parametric tests
 These tests are distribution free.
 Easier to calculate & less time consuming than parametric
tests when sample size is small.
 Can be used with any type of data.
 Many non-parametric methods make it possible to work
with very small samples, particularly helpful in collecting
pilot study data or medical researcher working with a rare
disease.
18

19. 19