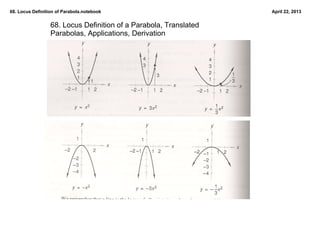
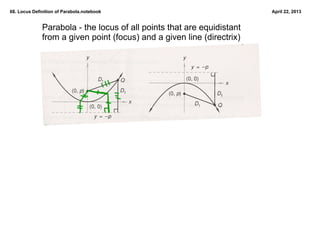
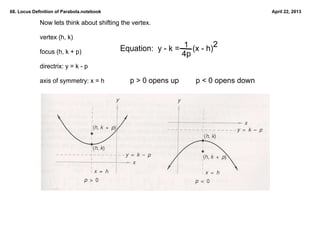
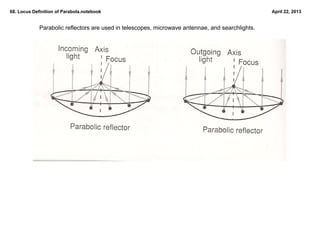
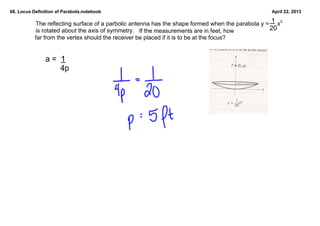
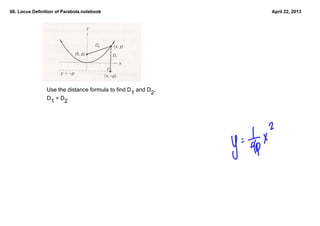
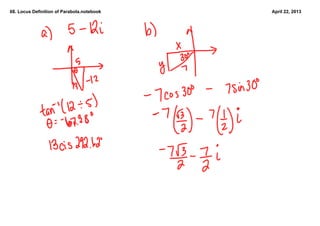This document defines and discusses parabolas using the locus definition. It states that a parabola is the locus of all points that are equidistant from a fixed point (the focus) and a fixed line (the directrix). The document provides examples of finding the equation of a parabola given the focus and directrix, as well as shifting the vertex. It also discusses applications of parabolic reflectors and how to place a receiver at the focus of a rotating parabolic antenna based on the given equation.

1. 68. Locus Definition of Parabola.notebook April 22, 2013
68. Locus Definition of a Parabola, Translated
Parabolas, Applications, Derivation
scan page 430 all pictures

2. 68. Locus Definition of Parabola.notebook April 22, 2013
Locus method of a line
A line is the locus of all the points equidistant from 2 points.
A circle is the locus of all points that are equidistant from the center.

3. 68. Locus Definition of Parabola.notebook April 22, 2013
Parabola ­ the locus of all points that are equidistant
from a given point (focus) and a given line (directrix)
scan pics p 431

4. 68. Locus Definition of Parabola.notebook April 22, 2013
For a parabola whose vertex is at the origin the equation is
1 2
y = x
4p
(0, 0) vertex
(0, p) coordinate of the focus
y = ­p equation of the directrix

5. 68. Locus Definition of Parabola.notebook April 22, 2013
1. Find the coordinates of the focus and the equation of the directrix for the parabola
3 2
y = x 1 2
y = x
7 4p
Focus (0, ) Directrix y =

6. 68. Locus Definition of Parabola.notebook April 22, 2013
2. The focus of a parabola has coordinates (0, ­5/3) and the vertex
is at the origin. Find the equation of the parabola and sketch it.
Focus: (0, p) 1 2
y = x
Directrix: y = ­p 4p
scan p 432

7. 68. Locus Definition of Parabola.notebook April 22, 2013
Now lets think about shifting the vertex.
vertex (h, k)
focus (h, k + p) Equation: y ­ k = (x ­ h)2
1
4p
directrix: y = k ­ p
axis of symmetry: x = h p > 0 opens up p < 0 opens down
scan p 433

8. 68. Locus Definition of Parabola.notebook April 22, 2013
(h, k) (h, k+p)
3. A parabola has a vertex of (­2, 1) and focus (­2, ­1). Write the equations for
the parabola, the directrix, and the axis of symmetry. Sketch the parabola.
y ­ k = (x ­ h)2
1 directrix: y = k­p
4p
aos: x = h

9. 68. Locus Definition of Parabola.notebook April 22, 2013
Parabolic reflectors are used in telescopes, microwave antennae, and searchlights.
scan p 434

10. 68. Locus Definition of Parabola.notebook April 22, 2013
1
The reflecting surface of a parbolic antenna has the shape formed when the parabola y = x2
is rotated about the axis of symmetry. If the measurements are in feet, how 20
far from the vertex should the receiver be placed if it is to be at the focus?
a = 1
4p

11. 68. Locus Definition of Parabola.notebook April 22, 2013
scan picture on page 435
Use the distance formula to find D1 and D2.
D1 = D2

12. 68. Locus Definition of Parabola.notebook April 22, 2013

13. 68. Locus Definition of Parabola.notebook April 22, 2013

14. 68. Locus Definition of Parabola.notebook April 22, 2013

15. 68. Locus Definition of Parabola.notebook April 22, 2013