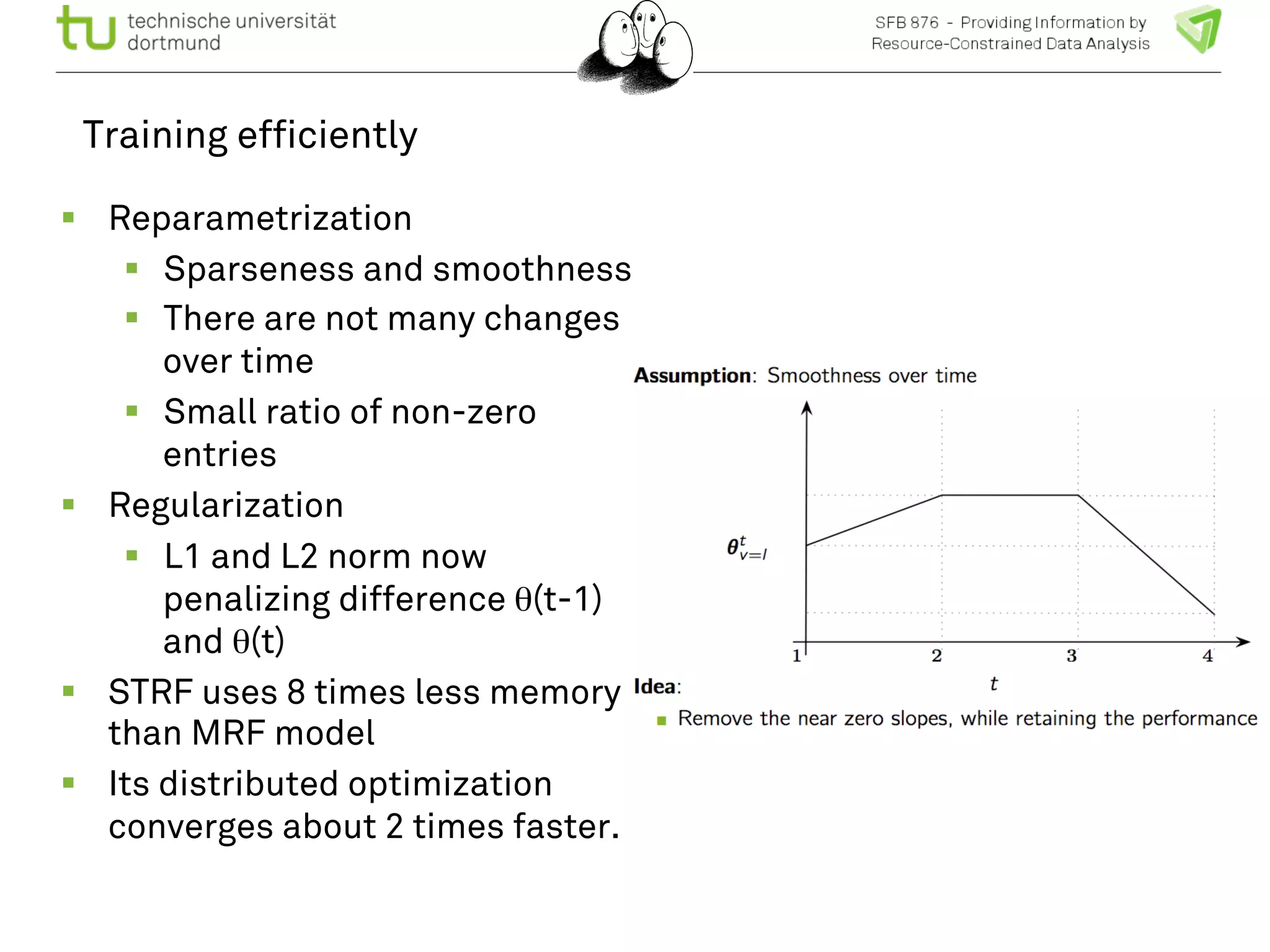
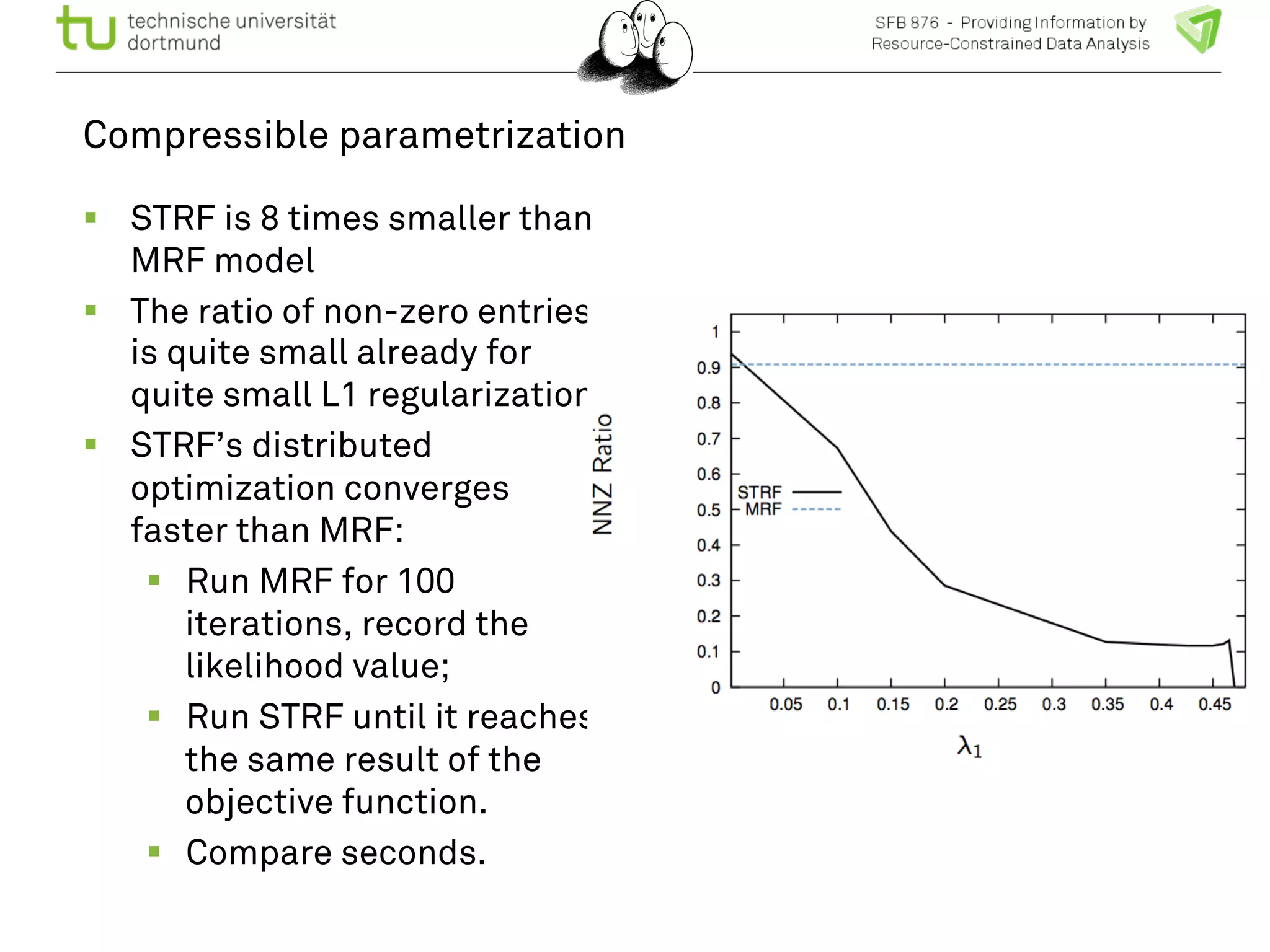
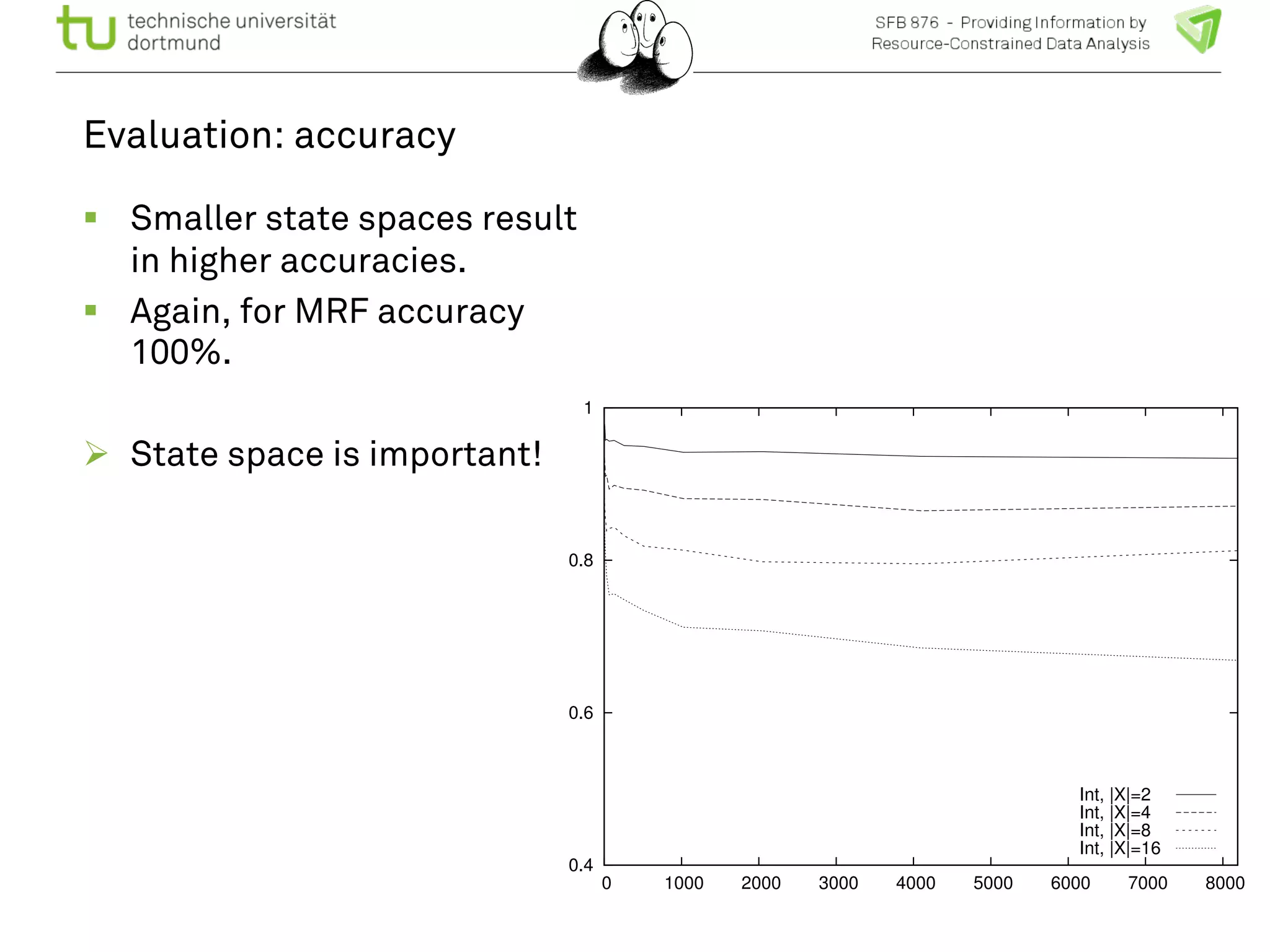
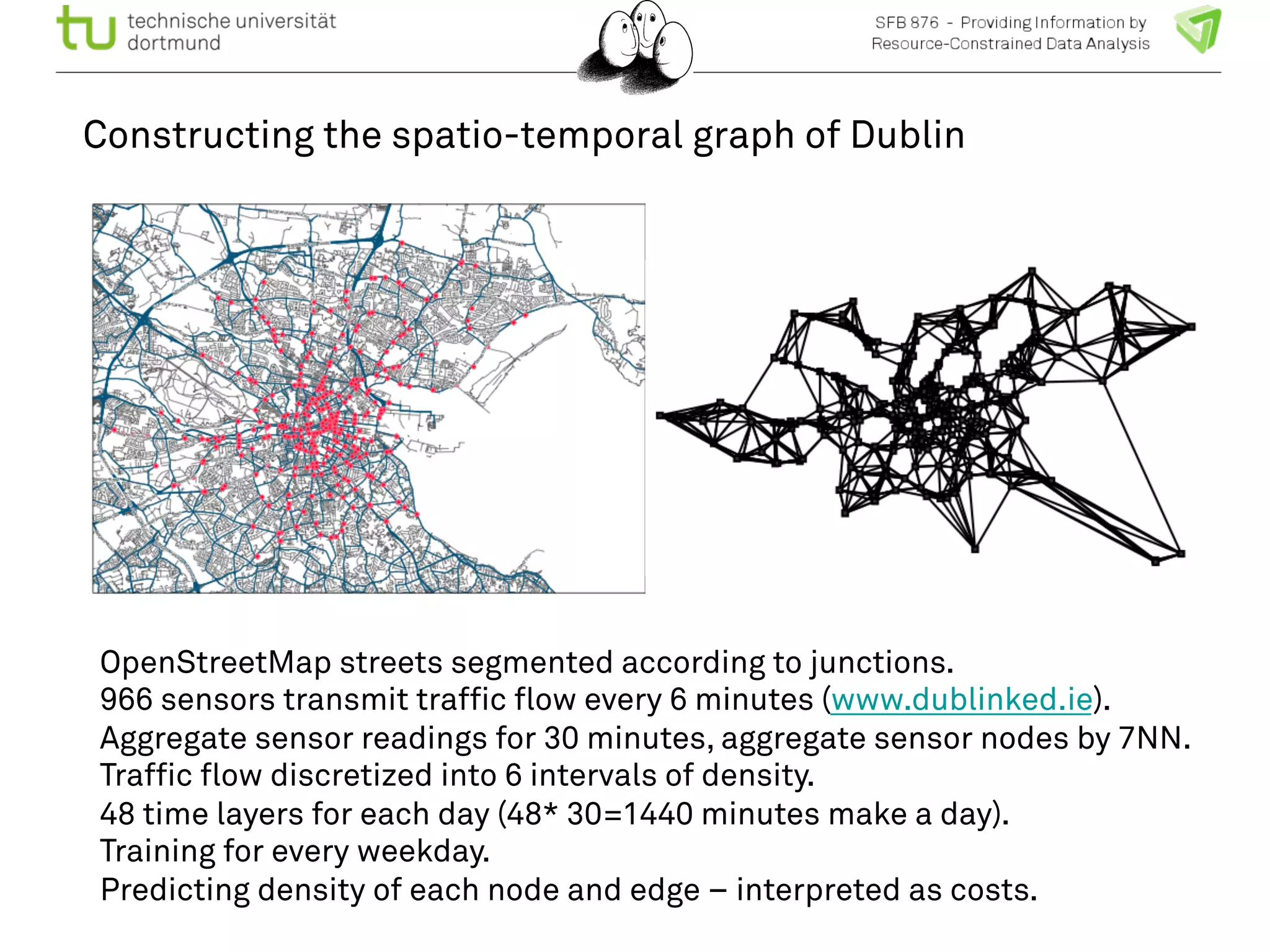
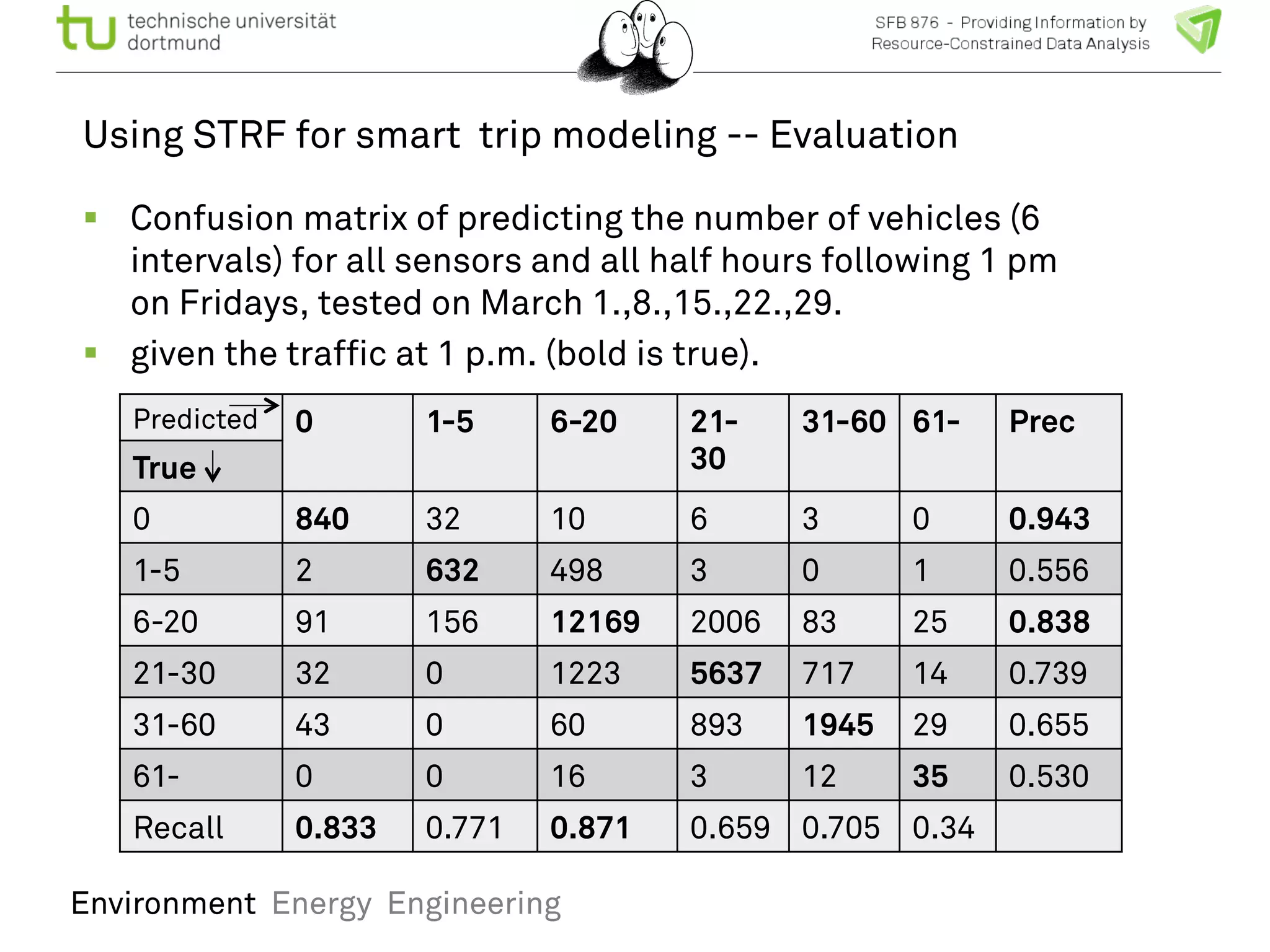
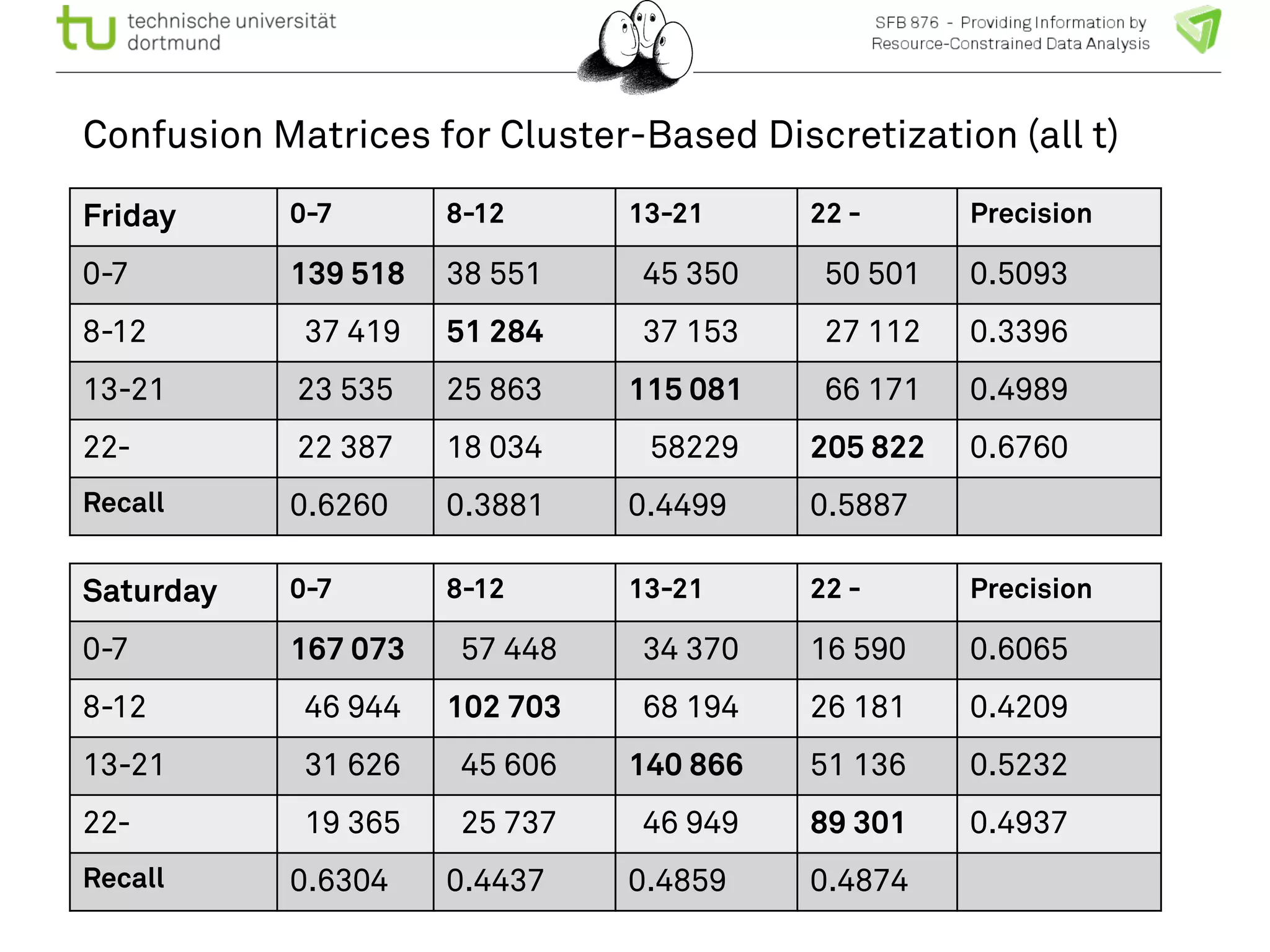
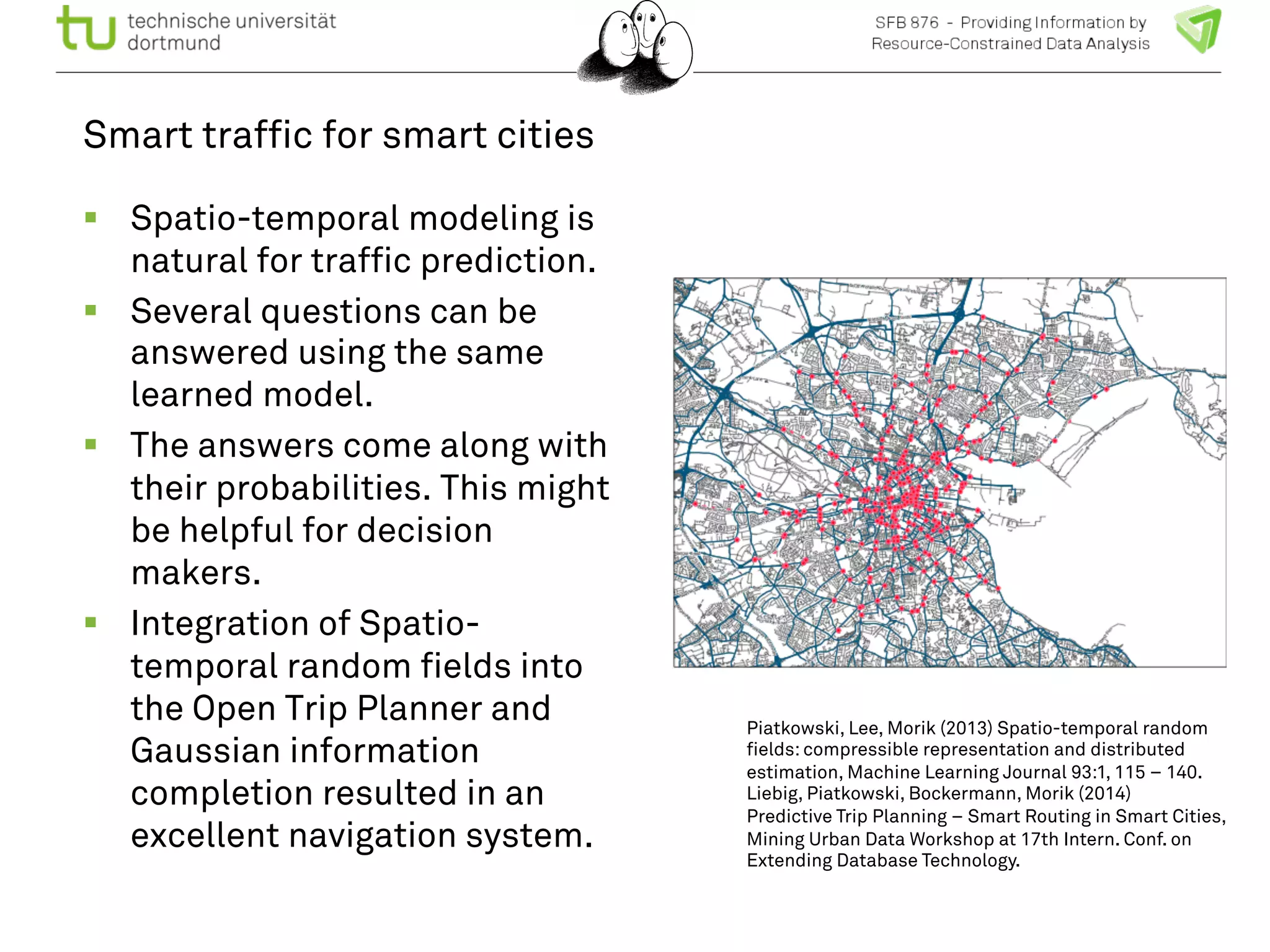
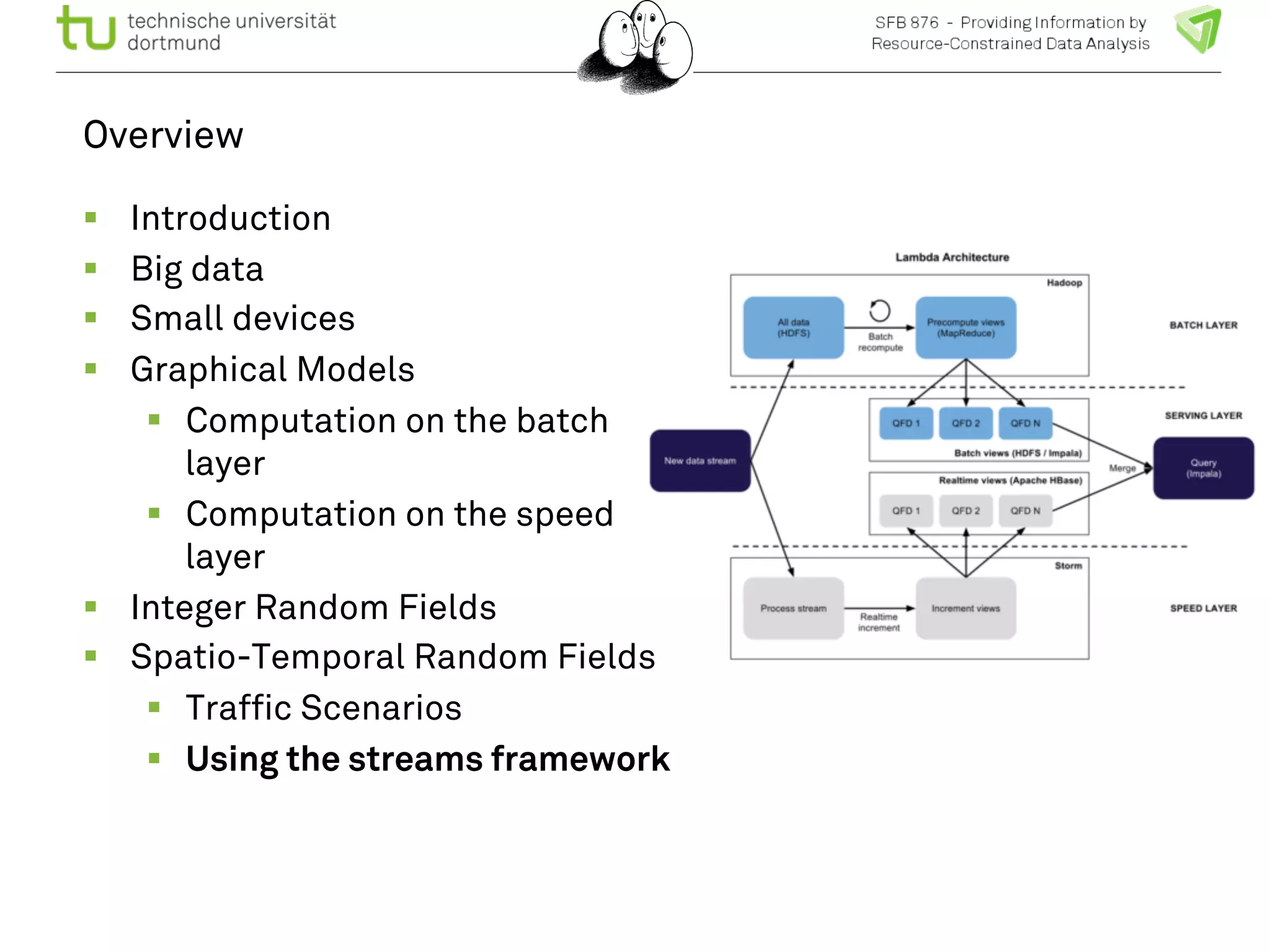
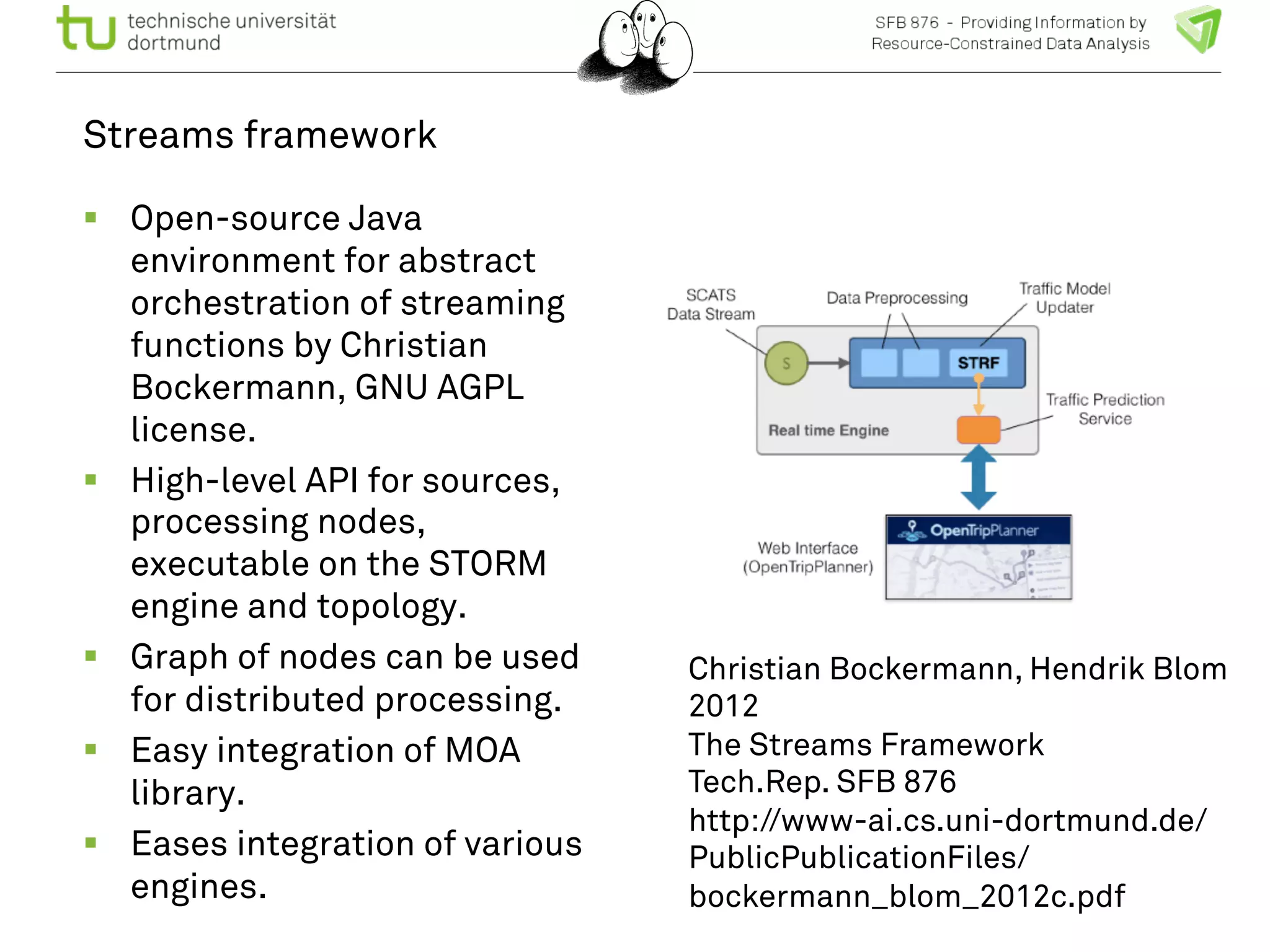
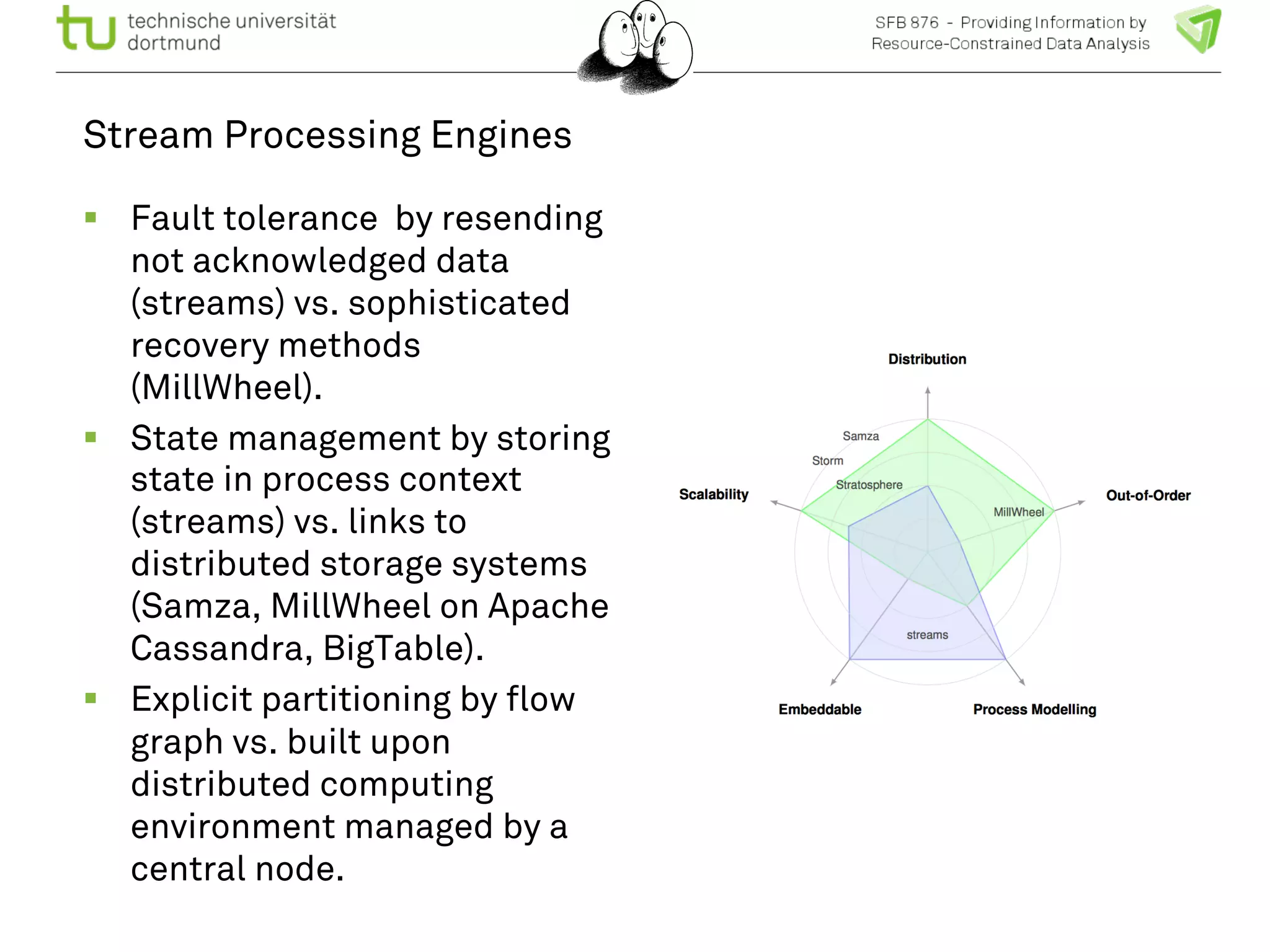
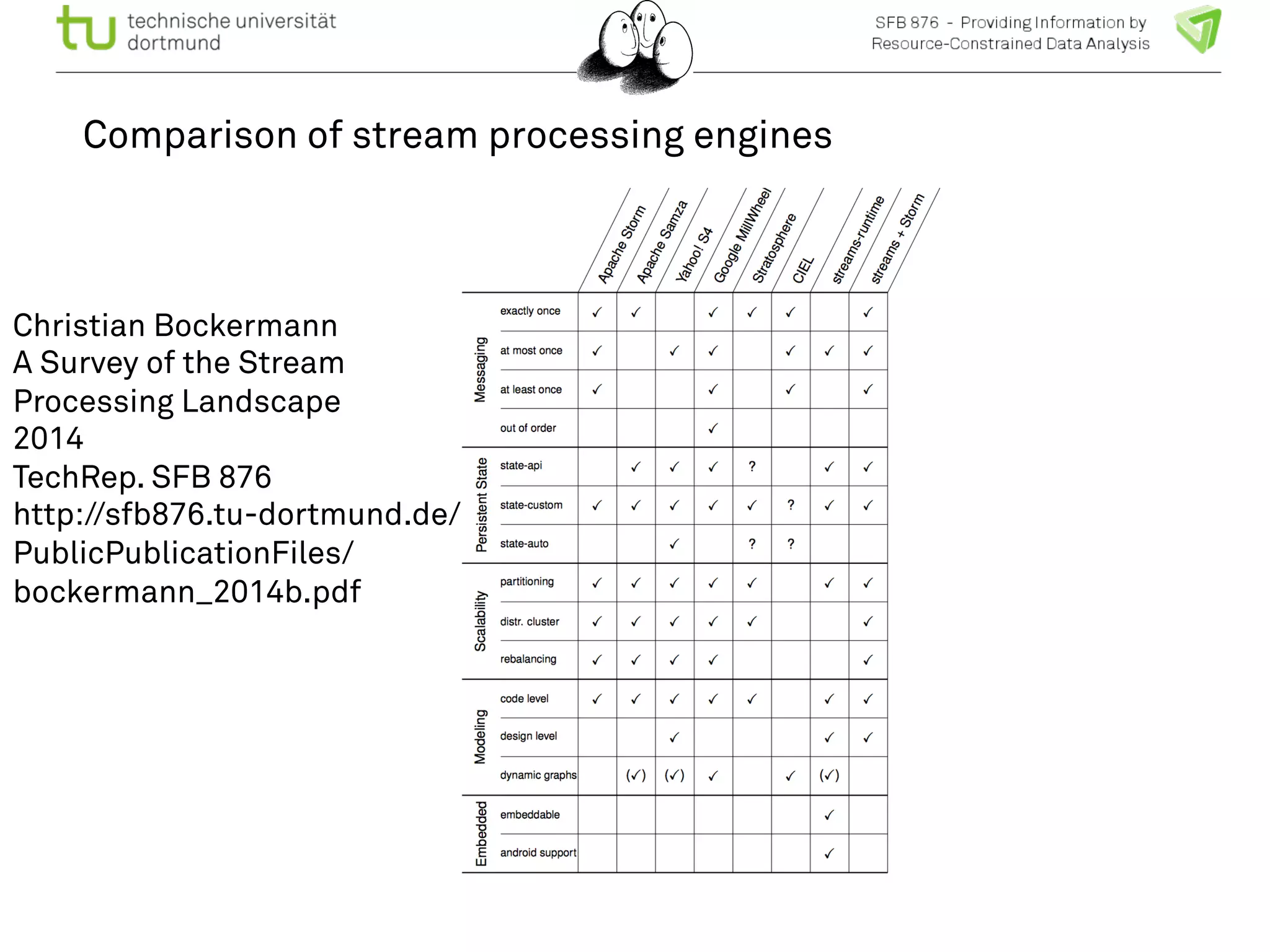
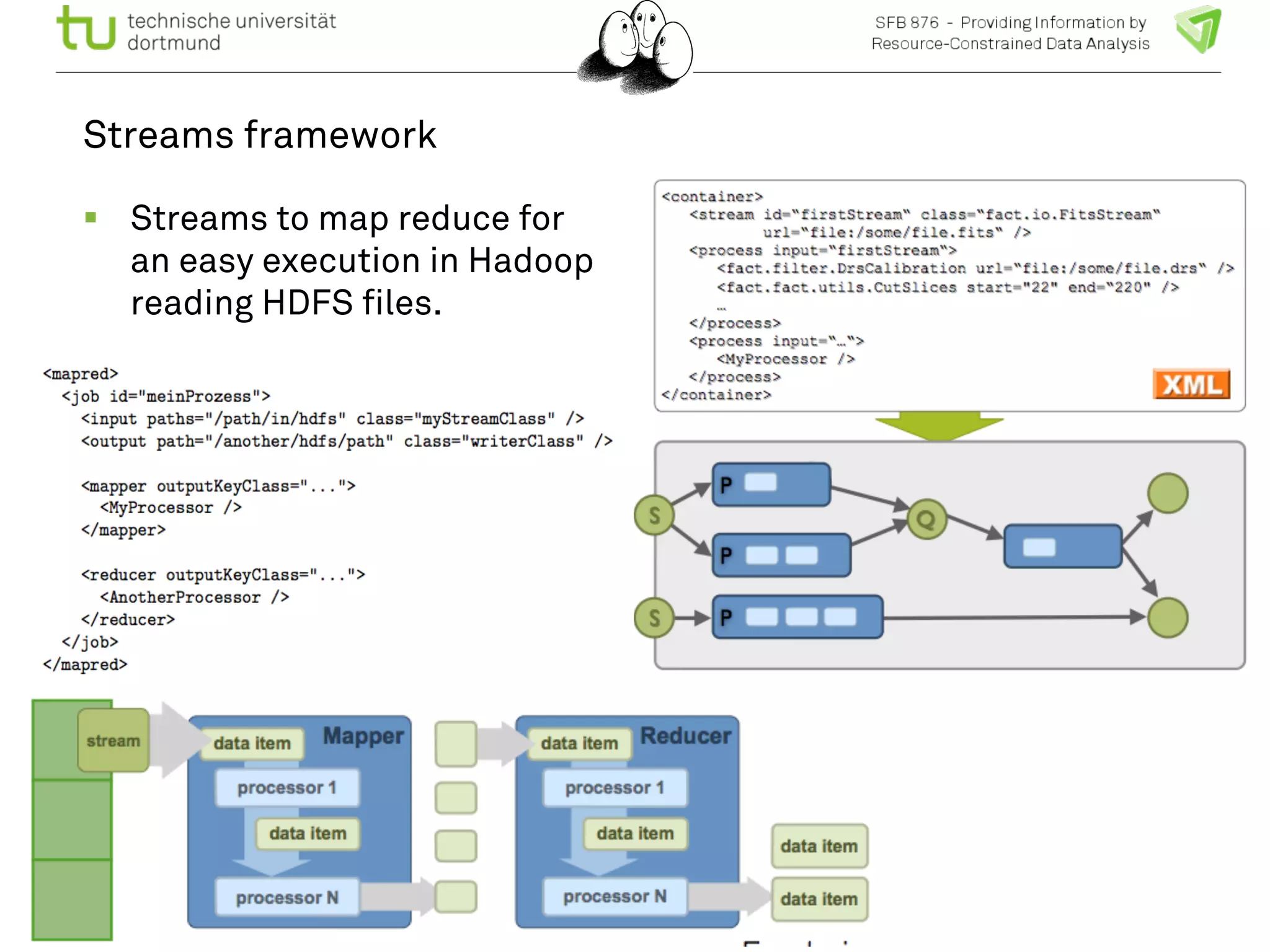
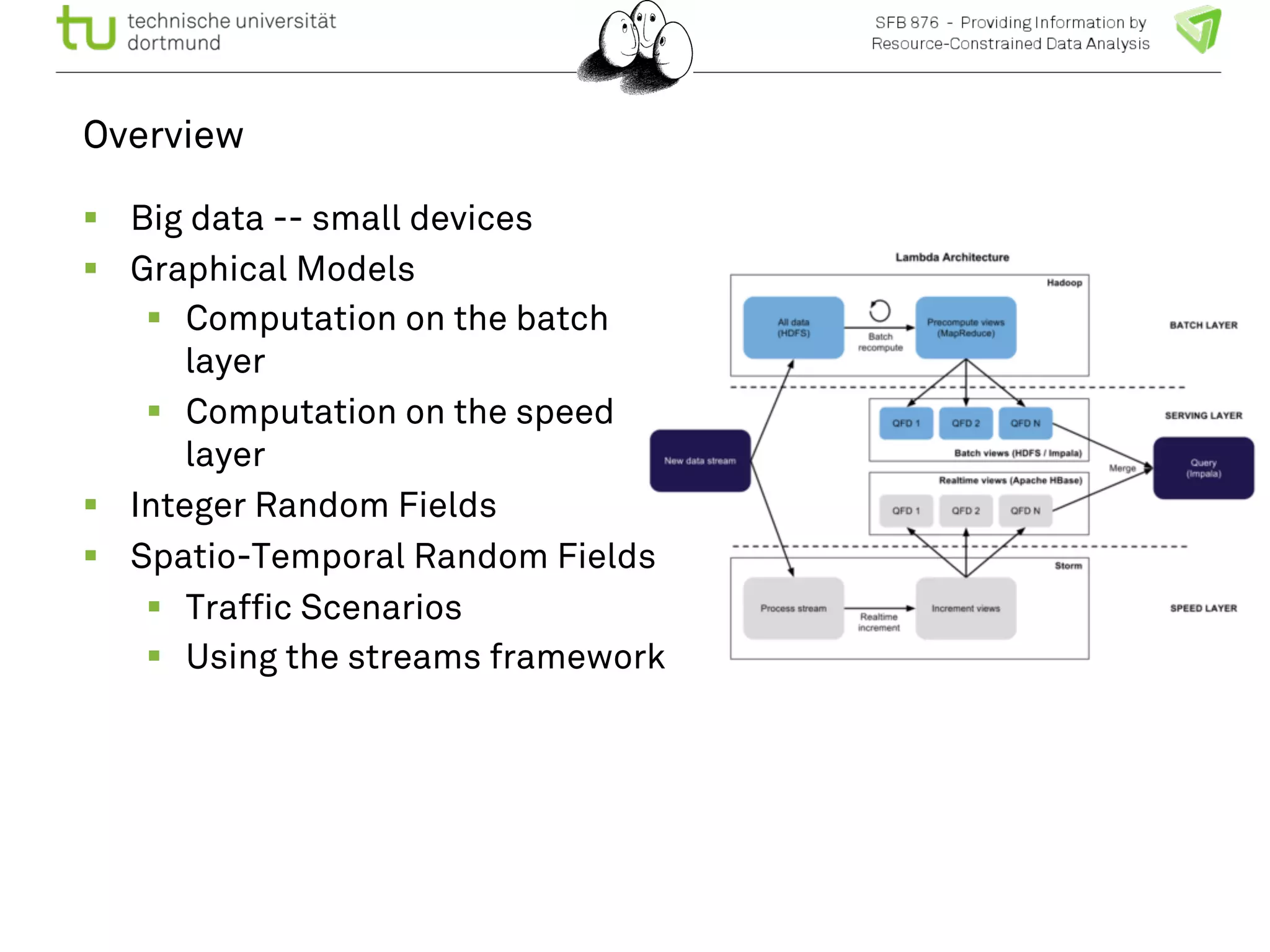
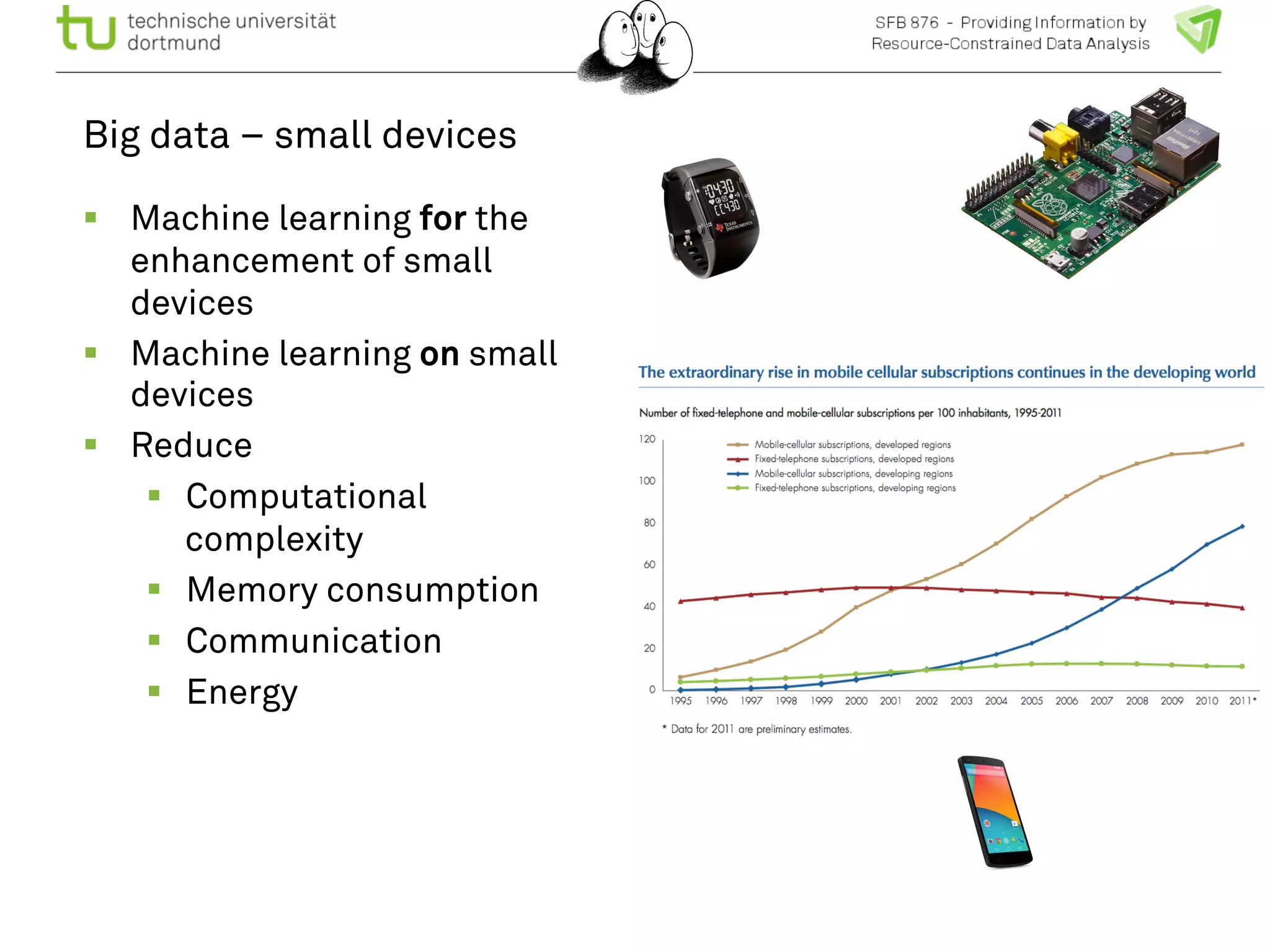
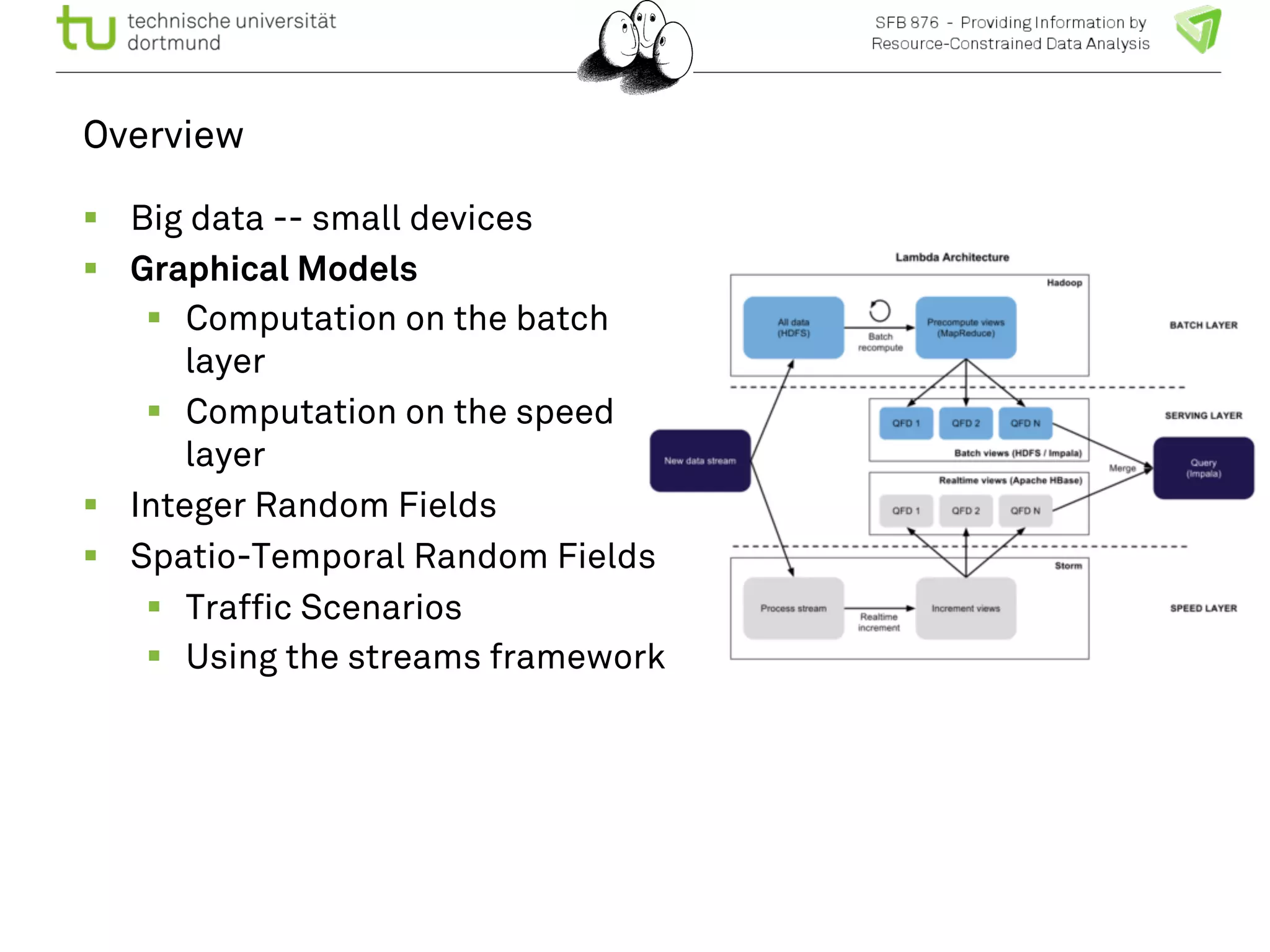
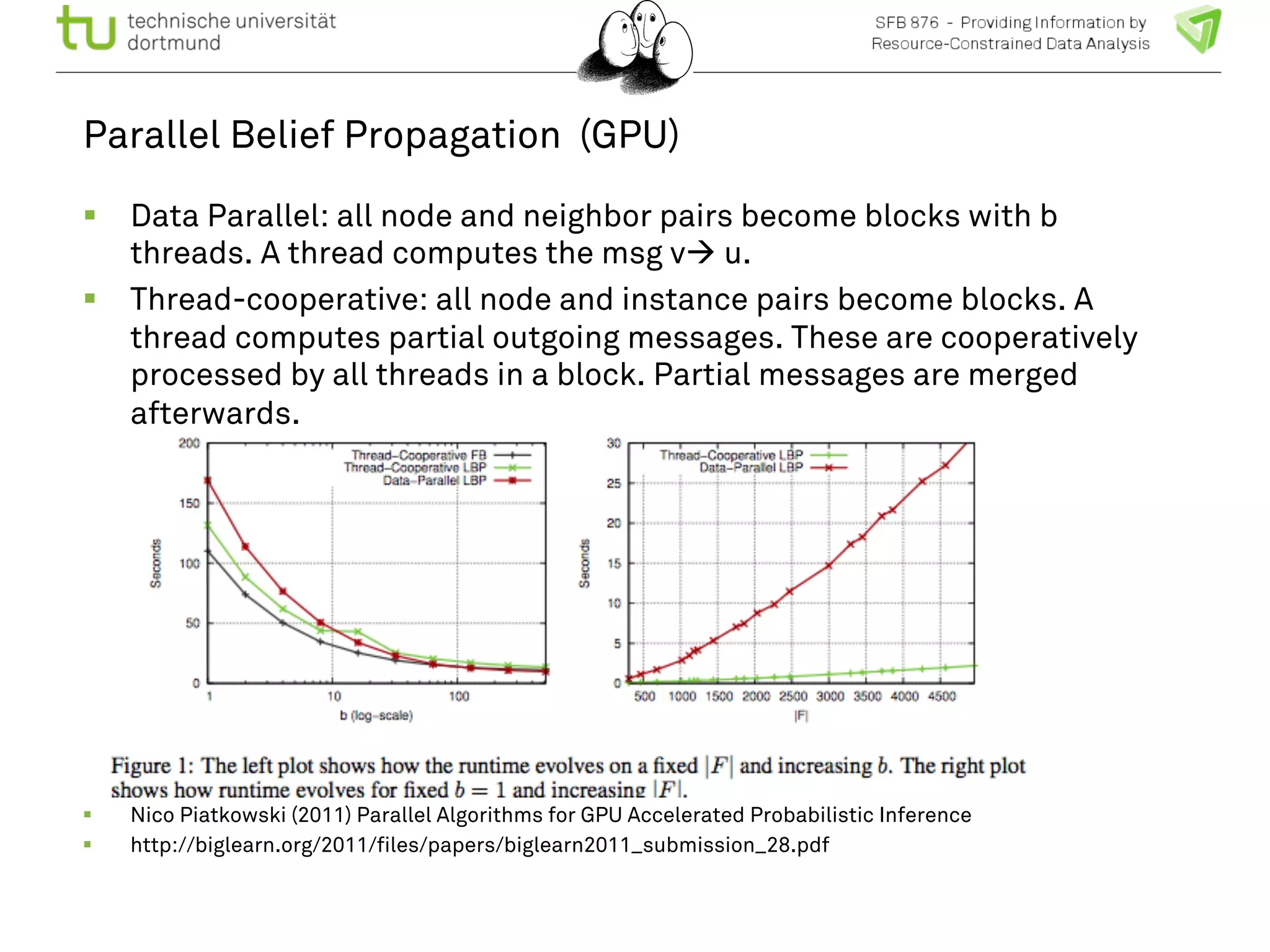
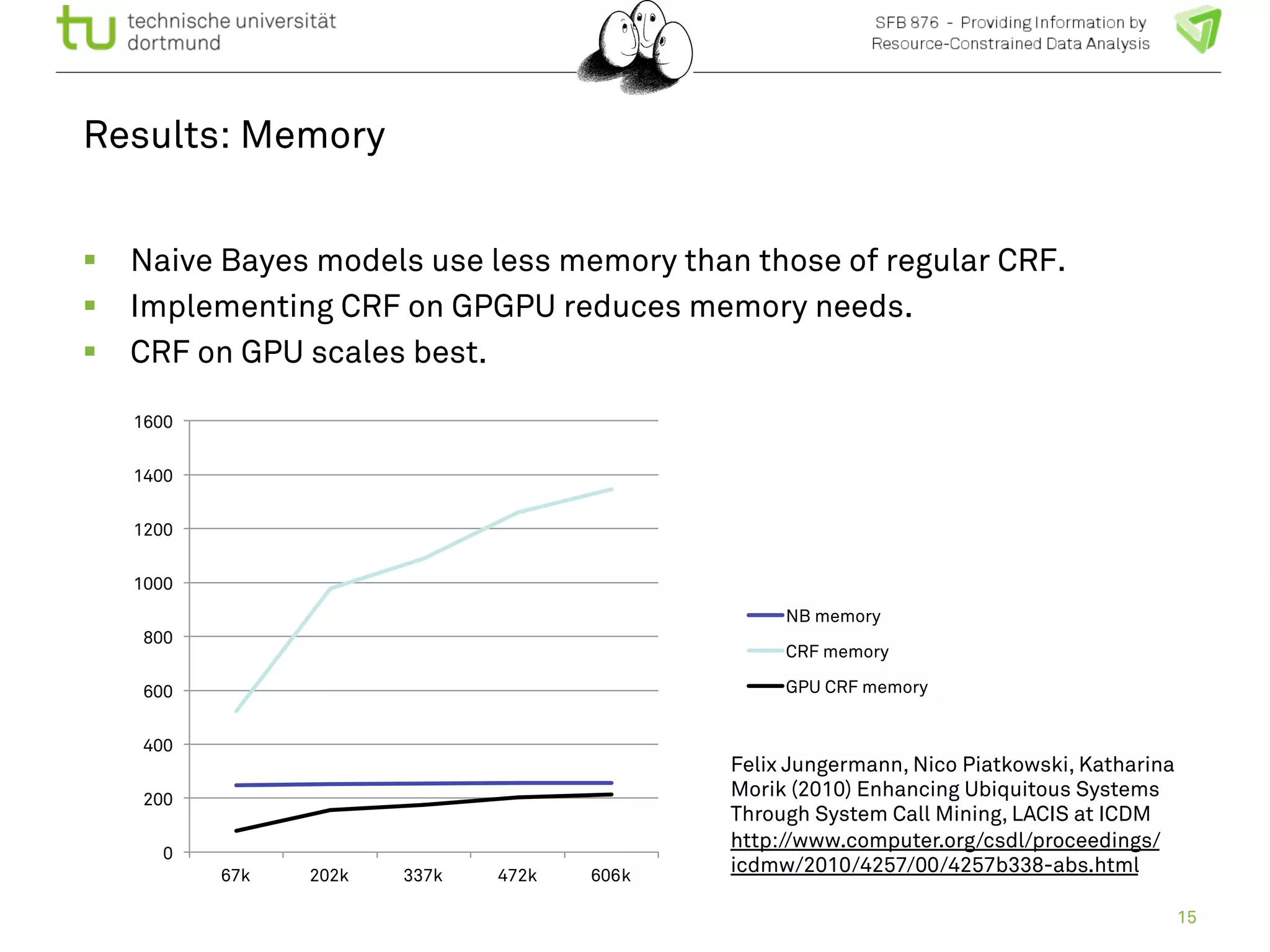
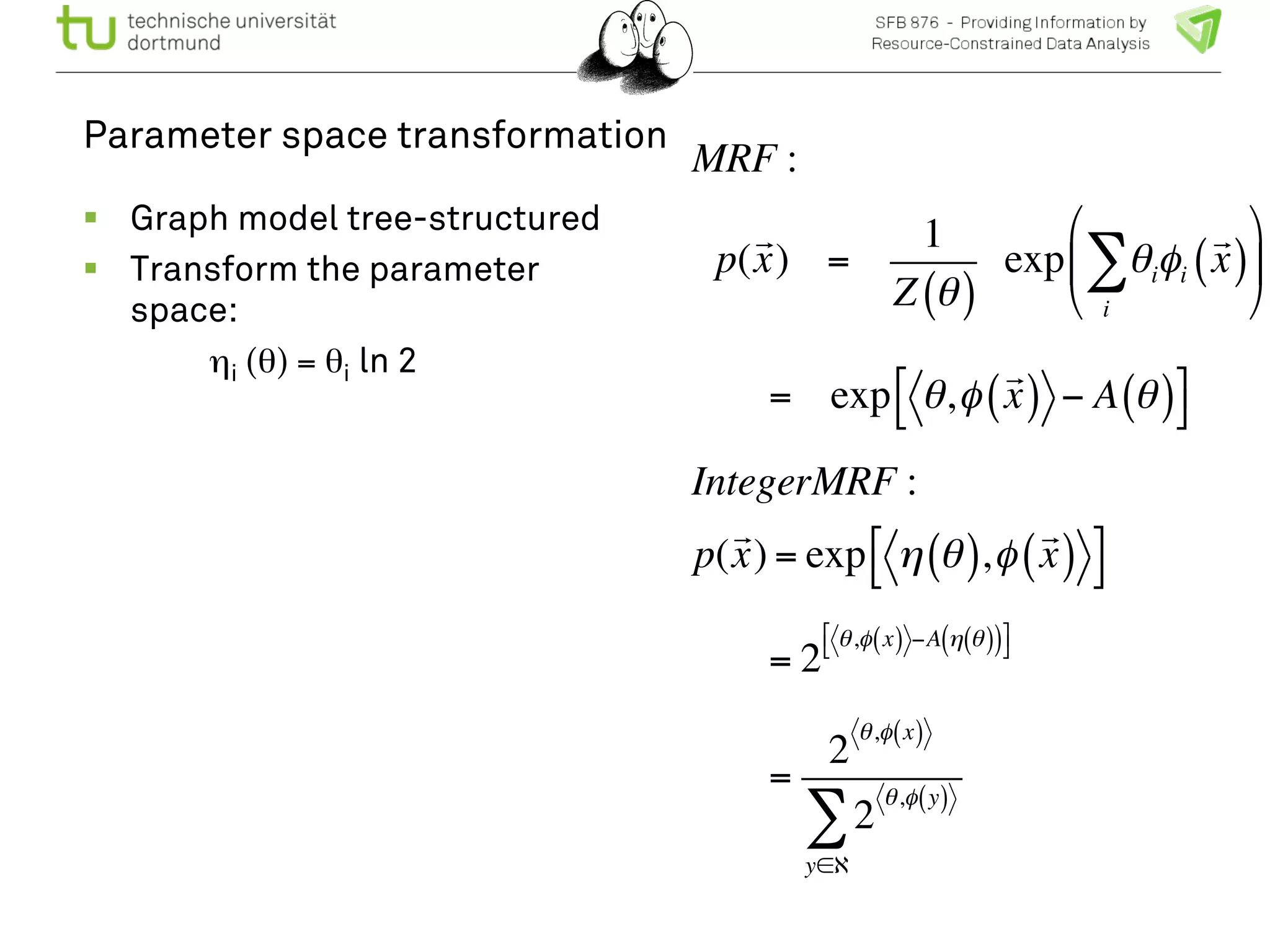
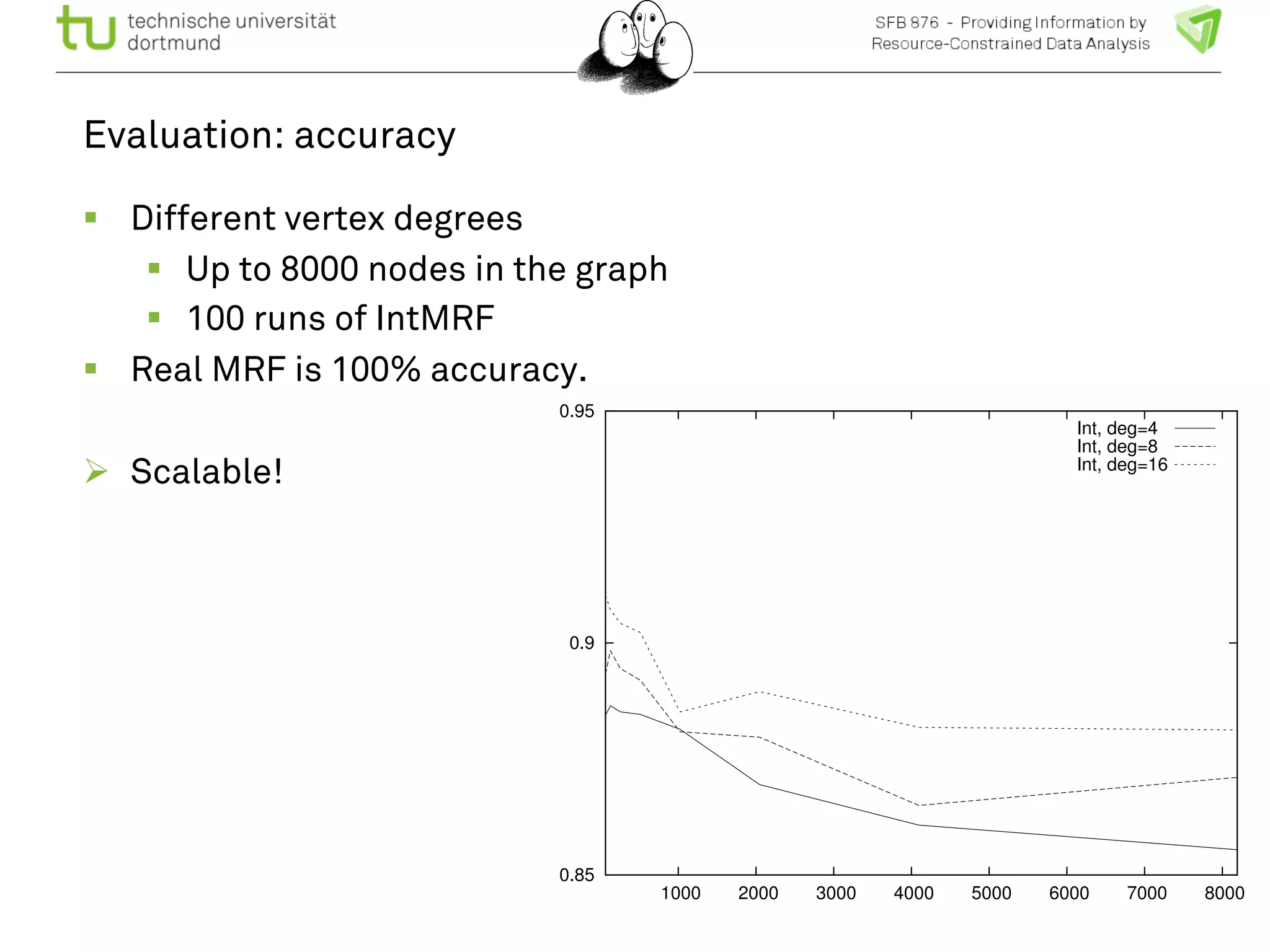
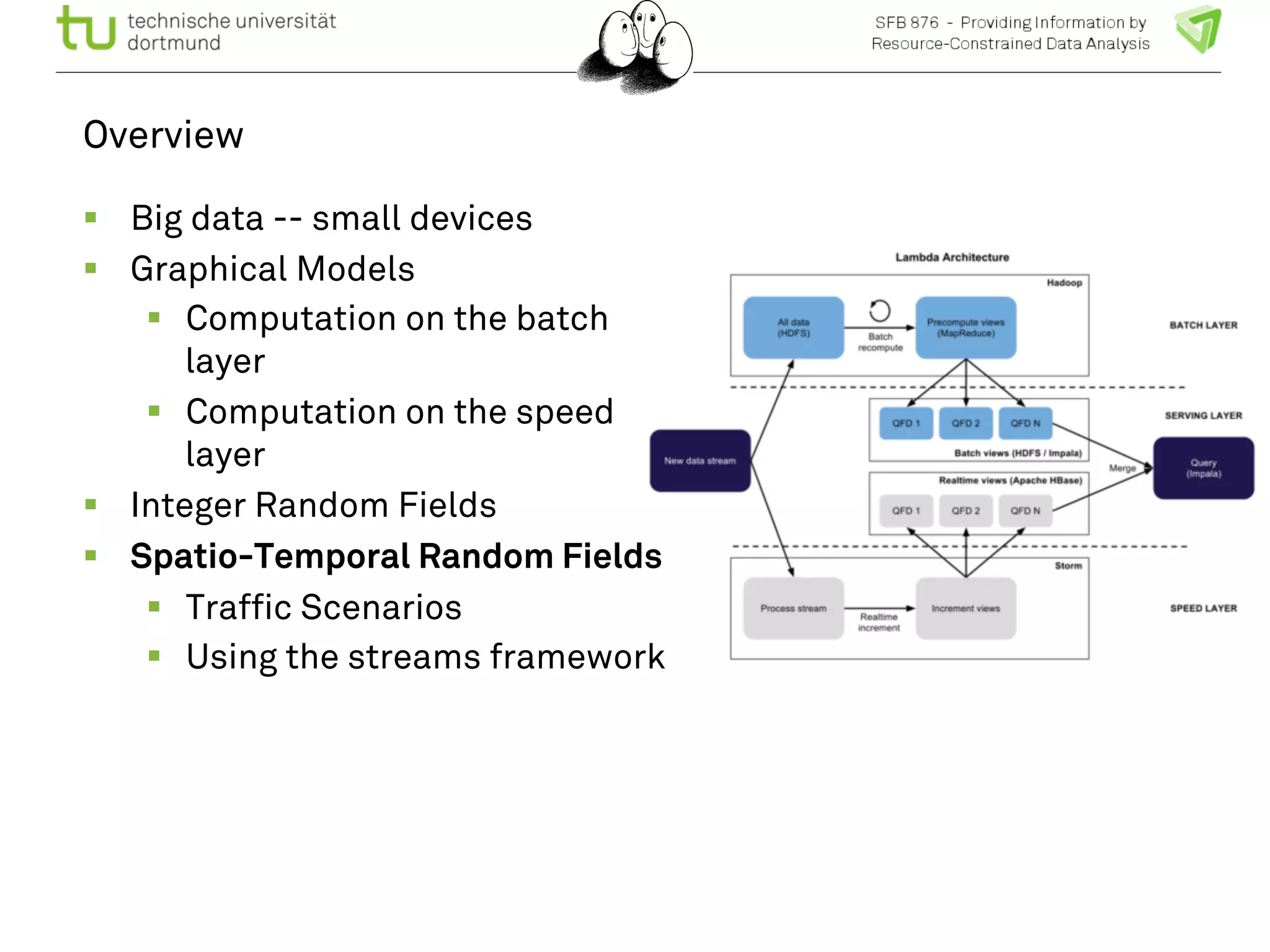
The document discusses the integration of big data and machine learning in enhancing small devices, particularly through the use of graphical models and spatio-temporal random fields for traffic prediction and automation. It highlights techniques for reducing computational complexity, memory consumption, and energy usage while performing probabilistic inference on resource-restricted devices. Additionally, it presents applications in smart traffic management systems and the development of a streaming framework for efficient data processing.

1. Big Data and Small Decives
Katharina Morik, Artificial Intelligence,
TU Dortmund University, Germany

2. Overview
! Big data -- small devices
! Graphical Models
! Computation on the batch
layer
! Computation on the speed
layer
! Integer Random Fields
! Spatio-Temporal Random Fields
! Traffic Scenarios
! Using the streams framework

3. Big data – small devices
! Machine learning for the
enhancement of small
devices
! Machine learning on small
devices
! Reduce
! Computational
complexity
! Memory consumption
! Communication
! Energy

4. Overview
! Big data -- small devices
! Graphical Models
! Computation on the batch
layer
! Computation on the speed
layer
! Integer Random Fields
! Spatio-Temporal Random Fields
! Traffic Scenarios
! Using the streams framework

5. Graphical Models
! Graph G=(V,E)
! Multi-variate random variable
X
with finite discrete domain X
! Mapping joint vertex
assignment into vector space
φ(x): X --> Rd
! Parameter to be learned:
θ in Rd
CRF :
p
( !
!
y
x) =
1
!
( x)
Z θ,
Σ
exp θi
φi
( !
x)
!
y,
i
"
# $
%
& '
1
a
= exp(−ln a)
Σ
= exp θi
φi
( !
x)
!
y,
i
"
# $
%
& '
!
( x)
− ln Z θ,
)
* +
,
- .
!
x ( ) − A θ ( ) )*
= exp θ,φ
!
y,
,-
MRF :
p(
!
x) =
1
Z θ ( )
Σ
exp θi
φi
!
(x)
i
"
# $
%
& '
!
x ( ) − A θ ( ) )*
= exp θ,φ
,-

6. Note: vectors are sparse
φ(x): ( /* Nodes*/
1. red, /*dom(lights)*/
2. yellow,
3. green,
4. wet, /*dom(rain)*/
5. dry,
6. jam, /*dom(jam)*/
7. free,
/*Edges*/
1. red, dry, /* edge lights-rain*/
2. yellow, dry,
3. green, dry,
4. red, wet,
5. yellow, wet,
6. green, wet,
7. red, jam, /*edge lights-jam*/
8. yellow, jam,
9. green, jam,
10. red, free,
11. yellow, free,
12. green, free,
13. dry, free, /*edge rain-jam*/
14. dry, jam,
15. wet, free,
16. wet, jam)
)
! x1:(red,dry,free)
Lights
Rain
Jam
{jam,
free}
{dry, wet}
{red,
yellow,
green}

7. Conditional Random Field: Likelihood

8. Markov Random Field: Likelihood

9. Markov Random Field: Estimation and Prediction

10. Belief propagation
! Actually computing the expected probability of parameters given θ by
message passing for each direction.

11. Note: vectors are sparse
φ(x): ( /* Nodes*/
1. red, /*dom(lights)*/
2. yellow,
3. green,
4. wet, /*dom(rain)*/
5. dry,
6. jam, /*dom(jam)*/
7. free,
/*Edges*/
1. red, dry, /* edge lights-rain*/
2. yellow, dry,
3. green, dry,
4. red, wet,
5. yellow, wet,
6. green, wet,
7. red, jam, /*edge lights-jam*/
8. yellow, jam,
9. green, jam,
10. red, free,
11. yellow, free,
12. green, free,
13. dry, free, /*edge rain-jam*/
14. dry, jam,
15. wet, free,
16. wet, jam)
)
! x1:(red,dry,free)
! φ(x1)=
(1,0,0,0,1,0,1,1,0,0,0,0,0,0,
0,0,1,0,0,1,0,0,0)
! d = 23
Lights
Rain
Jam
{jam,
free}
{dry, wet}
{red,
yellow,
green}

12. Belief propagation example
Π
Σ
mv→u (y) = exp θvu=xy +θv=x ( ) mwu (x)
Lights
Rain
Jam
{jam,
free}
{dry, wet}
{red,
yellow,
green}
w∈Nv−{u}
x∈ℵv
Compute for each node u
and each of its neighbors
and each of the states

13. Parallel Belief Propagation (GPU)
! Data Parallel: all node and neighbor pairs become blocks with b
threads. A thread computes the msg v" u.
! Thread-cooperative: all node and instance pairs become blocks. A
thread computes partial outgoing messages. These are cooperatively
processed by all threads in a block. Partial messages are merged
afterwards.
! Nico Piatkowski (2011) Parallel Algorithms for GPU Accelerated Probabilistic Inference
! http://biglearn.org/2011/files/papers/biglearn2011_submission_28.pdf

14. File Prefetching for Smartphone Energy Saving
! Accessing files that are stored in cache
consumes less energy than accessing those on the hard disc.
! Prefetching files which soon will be accessed
allows for grouping requests to a batched one. This saves energy.
" Prediction of file access saves energy!
Given a system call:
1,open,1812,179,178,201,200,firefox,/etc/hosts,524288,438,7
Predict: hosts full
Prefetch: hosts
2,read,1812,179,178,201,200,firefox,/etc/hosts,4096,361
3,read,1812,179,178,201,200,firefox,/etc/hosts,4096,0
4,close,1812,179,178,201,200,firefox,/etc/hosts
timestamp, syscall, thread-id, process-id, parent, user, group, exec, file,
parameters (optional)
14

15. Results: Memory
! Naive Bayes models use less memory than those of regular CRF.
! Implementing CRF on GPGPU reduces memory needs.
! CRF on GPU scales best.
15
1600
1400
1200
1000
800
600
400
200
0
67k 202k 337k 472k 606k
NB memory
CRF memory
GPU CRF memory
Felix Jungermann, Nico Piatkowski, Katharina
Morik (2010) Enhancing Ubiquitous Systems
Through System Call Mining, LACIS at ICDM
http://www.computer.org/csdl/proceedings/
icdmw/2010/4257/00/4257b338-abs.html

16. Overview
! Big data -- small devices
! Graphical Models
! Computation on the batch
layer
! Computation on the speed
layer
! Integer Random Fields
! Spatio-Temporal Random Fields
! Traffic Scenarios
! Using the streams framework

17. Graphical models on resource-restricted processors
! Floating point arithmetics
(real) costs more clock cycles
than integer arithmetics.
! “The most obvious technique
to conserve power is to
reduce the number of cycles
it takes to complete a
workload.” (Intel 64, IA-32
architectures optimization
reference manual, guidelines
for extending battery life).
! Restrict the parameter space
of MRF
Sandy Bridge ARM 11
Real Int Real Int
+ 3 1 8 1
* 5 3 8 4-5
/ 14 13-15 19 -
Bit
- 3 - 2
shift
Clock cycles for arithmetics
on different processors:
Real vs. integer.
θ ∈{0,1,...,K}⊂ Ν

18. Parameter space transformation
! Graph model tree-structured
! Transform the parameter
space:
ηi (θ) = θi ln 2
MRF :
p(
!
x) =
1
Z θ ( )
Σ
exp θi
φi
!
(x)
i
"
# $
%
& '
!
x ( ) − A θ ( ) )*
= exp θ,φ
+,
IntegerMRF :
p(
!
x) = exp η θ ( ),φ
!
x ( ) )*
+,
= 2
θ ,φ x ( ) −A η θ ( ) ( ) )*
+,
=
2 θ ,φ (x)
2 θ ,φ (y)
y∈ℵ
Σ

19. Integer belief propagation
! Simply replacing the exp(.) by 2(.) is not sufficient
! Overflows are normally avoided by normalization.
! Normalization is impossible in integer division.
! Magnitude of messages corresponds to probability
! Use the length of each message
! Bit-length is similar to log
Π
Σ
mv→u (y) = exp θvu=xy +θv=x ( ) mwu (x)
w∈Nv−{u}
x∈ℵv
m! v→u (y) = 2 (θvu=xy+θv=x )
Σ m! wu (x)
x∈ℵv
Π
w∈Nv−{u}
βv→u (y) = max
x∈ℵv
Σ
θvu=xy +θv=x + βwu (x)
w∈Nv−{u}

20. Evaluation: accuracy
0.95
0.9
0.85
Int, deg=4
Int, deg=8
Int, deg=16
1000 2000 3000 4000 5000 6000 7000 8000
! Different vertex degrees
! Up to 8000 nodes in the graph
! 100 runs of IntMRF
! Real MRF is 100% accuracy.
# Scalable!

21. Integer models use less clock cycles and memory
! Integer MRF shows
! high accuracy: 86 – 92%
of full MRF for up to 8
states and 8000 nodes
! high speed-up: 2.56
Raspberry Pie and 2.34
for Sandy Bridge
! Graphical models can now be
computed on small devices.
! Using less clock cycles really
saves energy.
Nico Piatkowski, Sangkyun Lee, Katharina Morik (2014)
The Integer Approximation of Undirected Graphical
Models, ICPRAM
http://www-ai.cs.uni-dortmund.de/
PublicPublicationFiles/piatkowski_etal_2014a.pdf

22. Overview
! Big data -- small devices
! Graphical Models
! Computation on the batch
layer
! Computation on the speed
layer
! Integer Random Fields
! Spatio-Temporal Random Fields
! Traffic Scenarios
! Using the streams framework

23. Spatio-temporal random fields
! The spatio-temporal graph is
trained to predict each node’s
maximum a posteriori
probability with the marginal
probabilities.
! Generative model predicting
all nodes.
! Dimension
T x |V0| x | X| +
[(T-1)(|V0|+3|E0|)+ |E0|] x |X|2
! Remember: vectors are sparse
we have to exploit that!
User queries:
Given traffic densities at all
nodes at t1, t2, t3, what is the
probability of traffic density
at node A at time t5?
Given state “jam” at place A
ts, which other places have a
higher probability for “jam” in
ts < t < te?

24. Training efficiently
! Reparametrization
! Sparseness and smoothness
! There are not many changes
over time
! Small ratio of non-zero
entries
! Regularization
! L1 and L2 norm now
penalizing difference θ(t-1)
and θ(t)
! STRF uses 8 times less memory
than MRF model
! Its distributed optimization
converges about 2 times faster.

25. Compressible parametrization
! STRF is 8 times smaller than
MRF model
! The ratio of non-zero entries
is quite small already for
quite small L1 regularization
! STRF’s distributed
optimization converges
faster than MRF:
! Run MRF for 100
iterations, record the
likelihood value;
! Run STRF until it reaches
the same result of the
objective function.
! Compare seconds.

26. Evaluation: accuracy
! Smaller state spaces result
in higher accuracies.
! Again, for MRF accuracy
100%.
# State space is important!
1
0.8
0.6
0.4
Int, |X|=2
Int, |X|=4
Int, |X|=8
Int, |X|=16
0 1000 2000 3000 4000 5000 6000 7000 8000

27. Flood in the City
! The city of Dublin suffers
from flood due to rainfall and
tide. Wanted:
! Optimal traffic
regulations based on
traffic predictions.
! Insight EU Project
www.insight-ict.eu
Intelligent Synthesis and
Real-time Response using
Massive Streaming of
Heterogeneous Data
Coordinator:
Dimitrios Gunopoulos, Univ.
Athens, Greece

28. Smart trip modeling for Dublin
! Open Street Map " graph
topology
! Open Trip Planner: user query
(v,w), route planning based on
traffic costs.
! Traffic costs learned:
! Spatio-temporal random
field based on sensor data
stream;
! Gaussian process estimates
values for non-sensor
locations.
! Framework for real-time
processing of data streams, XML
configuration of data flow,
connecting data, traffic model
and planner.
7:00
8:00
v
v
w
w

29. Constructing the spatio-temporal graph of Dublin
OpenStreetMap streets segmented according to junctions.
966 sensors transmit traffic flow every 6 minutes (www.dublinked.ie).
Aggregate sensor readings for 30 minutes, aggregate sensor nodes by 7NN.
Traffic flow discretized into 6 intervals of density.
48 time layers for each day (48* 30=1440 minutes make a day).
Training for every weekday.
Predicting density of each node and edge – interpreted as costs.

30. Using STRF for smart trip modeling -- Evaluation
! Confusion matrix of predicting the number of vehicles (6
intervals) for all sensors and all half hours following 1 pm
on Fridays, tested on March 1.,8.,15.,22.,29.
! given the traffic at 1 p.m. (bold is true).
Predicted 0 1-5 6-20 21-
30
31-60 61- Prec
True
0 840 32 10 6 3 0 0.943
1-5 2 632 498 3 0 1 0.556
6-20 91 156 12169 2006 83 25 0.838
21-30 32 0 1223 5637 717 14 0.739
31-60 43 0 60 893 1945 29 0.655
61- 0 0 16 3 12 35 0.530
Recall 0.833 0.771 0.871 0.659 0.705 0.34
Environment Energy Engineering

31. Confusion Matrices for Cluster-Based Discretization (all t)
Friday 0-7 8-12 13-21 22 - Precision
0-7 139 518 38 551 45 350 50 501 0.5093
8-12 37 419 51 284 37 153 27 112 0.3396
13-21 23 535 25 863 115 081 66 171 0.4989
22- 22 387 18 034 58229 205 822 0.6760
Recall 0.6260 0.3881 0.4499 0.5887
Saturday 0-7 8-12 13-21 22 - Precision
0-7 167 073 57 448 34 370 16 590 0.6065
8-12 46 944 102 703 68 194 26 181 0.4209
13-21 31 626 45 606 140 866 51 136 0.5232
22- 19 365 25 737 46 949 89 301 0.4937
Recall 0.6304 0.4437 0.4859 0.4874

32. Smart traffic for smart cities
! Spatio-temporal modeling is
natural for traffic prediction.
! Several questions can be
answered using the same
learned model.
! The answers come along with
their probabilities. This might
be helpful for decision
makers.
! Integration of Spatio-temporal
random fields into
the Open Trip Planner and
Gaussian information
completion resulted in an
excellent navigation system.
Piatkowski, Lee, Morik (2013) Spatio-temporal random
fields: compressible representation and distributed
estimation, Machine Learning Journal 93:1, 115 – 140.
Liebig, Piatkowski, Bockermann, Morik (2014)
Predictive Trip Planning – Smart Routing in Smart Cities,
Mining Urban Data Workshop at 17th Intern. Conf. on
Extending Database Technology.

33. Overview
! Introduction
! Big data
! Small devices
! Graphical Models
! Computation on the batch
layer
! Computation on the speed
layer
! Integer Random Fields
! Spatio-Temporal Random Fields
! Traffic Scenarios
! Using the streams framework

34. Streams framework
! Open-source Java
environment for abstract
orchestration of streaming
functions by Christian
Bockermann, GNU AGPL
license.
! High-level API for sources,
processing nodes,
executable on the STORM
engine and topology.
! Graph of nodes can be used
for distributed processing.
! Easy integration of MOA
library.
! Eases integration of various
engines.
Christian Bockermann, Hendrik Blom
2012
The Streams Framework
Tech.Rep. SFB 876
http://www-ai.cs.uni-dortmund.de/
PublicPublicationFiles/
bockermann_blom_2012c.pdf

35. Stream Processing Engines
! Fault tolerance by resending
not acknowledged data
(streams) vs. sophisticated
recovery methods
(MillWheel).
! State management by storing
state in process context
(streams) vs. links to
distributed storage systems
(Samza, MillWheel on Apache
Cassandra, BigTable).
! Explicit partitioning by flow
graph vs. built upon
distributed computing
environment managed by a
central node.

36. Comparison of stream processing engines
Christian Bockermann
A Survey of the Stream
Processing Landscape
2014
TechRep. SFB 876
http://sfb876.tu-dortmund.de/
PublicPublicationFiles/
bockermann_2014b.pdf

37. Streams framework
! Streams to map reduce for
an easy execution in Hadoop
reading HDFS files.

38. Conclusion
! Complex models such as MRF
can be computed on small
devices such as smartphones.
! Graphical Models
! Parallel BP using GPU
! Approximation to Integer
Random Fields
! Spatio-Temporal Random
Fields
! Using the streams
framework for integrating
processes (e.g. MOA for
learning) and real-time
processing and
documentation.

39. References
! Nico Piatkowski (2011) Parallel Algorithms
for GPU Accelerated Probabilistic
Inference
http://biglearn.org/2011/files/papers/
biglearn2011_submission_28.pdf
! Felix Jungermann, Nico Piatkowski,
Katharina Morik (2010) Enhancing
Ubiquitous Systems Through System Call
Mining, LACIS at ICDM
http://www.computer.org/csdl/proceedings/
icdmw/2010/4257/00/4257b338-abs.html
! Nico Piatkowski, Sangkyun Lee, Katharina
Morik (2014) The Integer Approximation of
Undirected Graphical Models, ICPRAM
http://www-ai.cs.uni-dortmund.de/
PublicPublicationFiles/
piatkowski_etal_2014a.pdf
! Piatkowski, Lee, Morik (2013) Spatio-temporal
random fields: compressible
representation and distributed
estimation, Machine Learning Journal
93:1, 115 – 140.
! Liebig, Piatkowski, Bockermann, Morik
(2014) Predictive Trip Planning – Smart
Routing in Smart Cities, Mining Urban
Data Workshop at 17th Intern. Conf. on
Extending Database Technology.
! Streams framework
Christian Bockermann, Hendrik Blom
2012 The Streams Framework
Tech.Rep. SFB 876
http://www-ai.cs.uni-dortmund.de/
PublicPublicationFiles/
bockermann_blom_2012c.pdf
! Christian Bockermann (2014) A Survey of
the Stream Processing Landscape
TechRep. SFB 876
http://sfb876.tu-dortmund.de/
PublicPublicationFiles/
bockermann_2014b.pdf
! For streams software (not just scripts!)
check:
http://www-ai.cs.uni-dortmund.de/
SOFTWARE/streams/