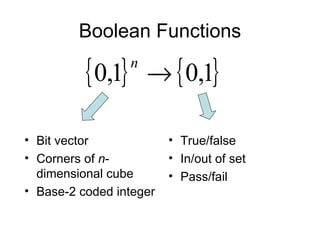
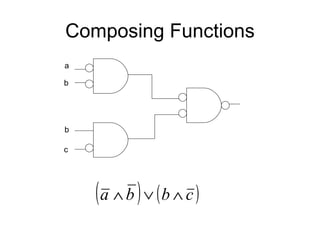
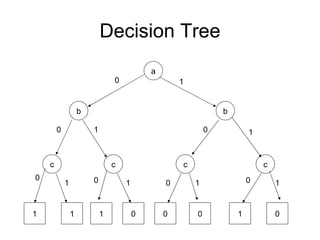
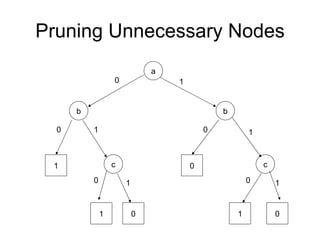
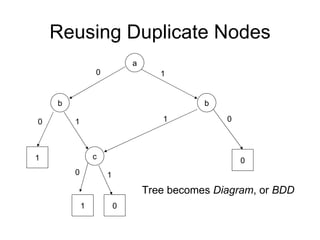
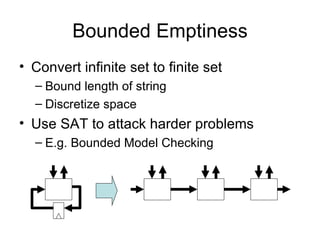
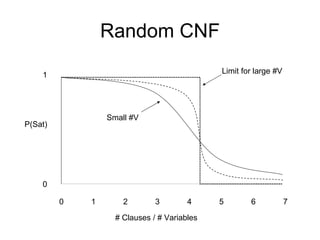
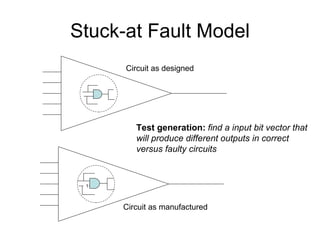
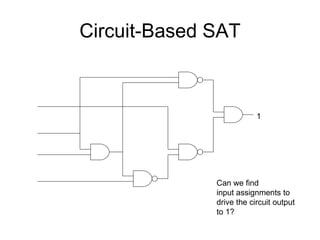
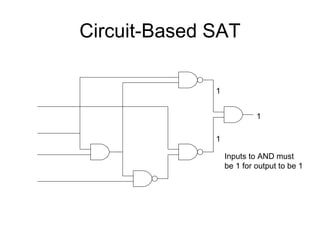
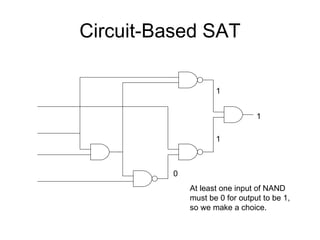
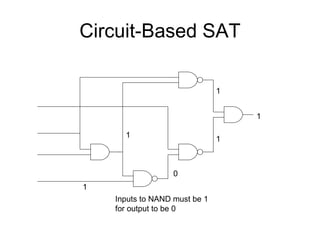
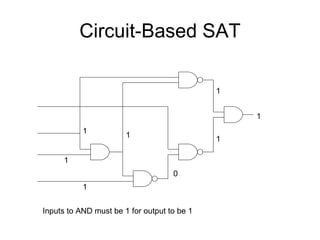
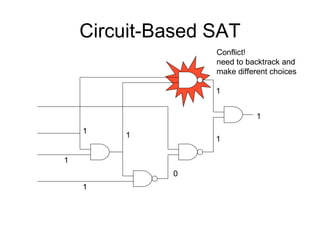
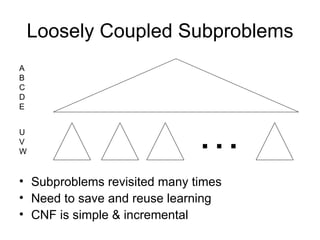
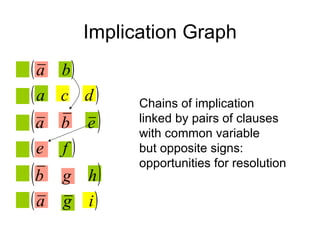
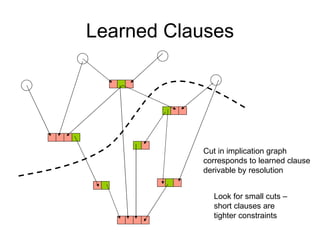
The document discusses applications and algorithms for satisfiability problems in Boolean logic and functions. It covers topics such as truth tables, composing functions, optimization, decision trees, binary decision diagrams, satisfiability communities and conferences, SAT file formats, and algorithms like resolution, variable elimination, local search, and circuit-based value assignment.

1. Satisfiability: Applications and Algorithms Jim Kukula [email_address]

2. Outline Boolean functions and expressions Applications and related formalisms Satisfiability Algorithms Expression-Based Assignment-Based

3. Boolean Functions Bit vector Corners of n -dimensional cube Base-2 coded integer True/false In/out of set Pass/fail

4. Truth Table Read-only memory is like this: Addr_in -> data_out 16 address bits enough to store a book No way, in general, to squeeze n bit values into any smaller space a b c

5. Composing Functions a b b c

6. Logic Optimization Very difficult to find optimal expression for a given Boolean function Gate count Longest path from input to output Any function has infinite expressions Most functions require exponential space Counting argument: Boolean functions with n variables

7. 2-Level Expressions DNF: Disjunctive Normal Form CNF: Conjunctive Normal Form

8. Decision Tree a b b c c c c 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1

9. Pruning Unnecessary Nodes a b b c c 1 1 0 0 1 0 0 0 0 0 0 1 1 1 1 1

10. Reusing Duplicate Nodes a b b c 1 1 0 0 0 0 0 0 1 1 1 1 Tree becomes Diagram , or BDD

11. Binary Decision Diagrams Breakthrough paper Randy Bryant, Graph - Based Algorithms for Boolean Function Manipulation . IEEE Transaction on Computers, 1986 http:// vlsi.colorado.edu/~fabio/CUDD / High quality public package

12. BDD Manipulation BDDs are canonical, given variable order Trivial to check function equality, satisfiability Often compact Optimizing variable order is difficult Interleave bits of an adder! BDD for (f&g) can be computed efficiently, from BDD for f and BDD for g

13. Formalized Decisions Boolean Functions Set of fixed length strings State Machines Regular languages Turing Machines Universal computability

14. Computational Problems Optimizing expressions Language in which machine expressed Optimality criteria Language Emptiness Boolean Functions NP-Complete Finite State Machines P-Space Complete Turing Machines Undecidable

15. Applications for Satisfiability Given a Boolean function, find an input bit vector for which the function evaluates to 1 Artificial Intelligence E.g. medical diagnosis Operations Research Optimizing over discrete domains Electronics Engineering Detecting faults Computer Science Check resource contention

16. Bounded Emptiness Convert infinite set to finite set Bound length of string Discretize space Use SAT to attack harder problems E.g. Bounded Model Checking

17. Satisfiability Community International Conference on Theory and Applications of Satisfiability Testing http://ie.technion.ac.il/SAT10/ (Edinburgh) Journal on Satisfiability, Boolean Modeling and Computation http:// www.isa.ewi.tudelft.nl/Jsat / Up-to-date links concerning research http:// www.satlive.org /

18. Dimacs Format p cnf 59056 323700 1 2 0 1 3 0 1 4 0 1 -5 0 1 6 0 1 -7 0 1 -8 0 1 -9 0 1 -10 0 -2 -3 -4 5 -6 7 8 9 10 -1 0 -11 -12 -13 14 0 -14 11 0 -14 12 0 -14 13 0

19. Random CNF P(Sat) 1 0 # Clauses / # Variables 1 0 2 3 4 5 6 7 Limit for large #V Small #V

20. Algorithms CNF Resolution BDD variable elimination Local Search Circuit-based value assignment Conflict-based Learning

21. Resolution Exhaustive application will yield empty clause if problem is unsatisfiable 3 n potential clauses!

22. BDD Variable Elimination Construction of BDD from circuit often infeasible Intermediate blow-up even if ultimate answer is trivial Interleave existential quantification Eliminating variables often reduces BDD sizes Finding an order of variables to eliminate is difficult Keep the support sizes small of intermediate results Equivalent to elimination with sparse matrices

23. Local Search Generally implemented with CNF Start by assigning arbitrary value to each variable Flip values of variables one by one Any variable that appears in a false clause is a candidate Gradually reduce number of false clauses Need mechanism to escape local minima No proof of unsatisfiability

24. Stuck-at Fault Model Circuit as designed Circuit as manufactured Test generation: find a input bit vector that will produce different outputs in correct versus faulty circuits 1

25. Circuit-Based SAT 1 Can we find input assignments to drive the circuit output to 1?

26. Circuit-Based SAT 1 1 1 Inputs to AND must be 1 for output to be 1

27. Circuit-Based SAT 1 1 1 0 At least one input of NAND must be 0 for output to be 1, so we make a choice.

28. Circuit-Based SAT 1 1 1 1 0 1 Inputs to NAND must be 1 for output to be 0

29. Circuit-Based SAT 1 1 1 1 0 1 1 1 Inputs to AND must be 1 for output to be 1

30. Circuit-Based SAT 1 1 1 1 0 1 1 1 Conflict! need to backtrack and make different choices

31. Loosely Coupled Subproblems Subproblems revisited many times Need to save and reuse learning CNF is simple & incremental … A B C D E U V W

32. Landmark Papers in CNF SAT Joao Marques-Silva and Karem Sakallah, “ GRASP: A Search Algorithm for Propositional Satisfiability ,” ICCAD 1996 Matthew W. Moskewicz, Conor F. Madigan, Ying Zhao, Lintao Zhang, Sharad Malik, “ Chaff: Engineering an Efficient SAT Solver, ” DAC 2001

33. CNF Decision & Implication Decide:

34. CNF Decision & Implication Decide: Imply:

35. CNF Decision & Implication Decide: Imply: Imply:

36. CNF Decision & Implication Decide: Imply: Imply: Imply:

37. CNF Decision & Implication Decide: Imply: Imply: Imply: Decide:

38. CNF Decision & Implication Decide: Imply: Imply: Imply: Decide: Imply:

39. Implication Graph Chains of implication linked by pairs of clauses with common variable but opposite signs: opportunities for resolution

40. Learned Clauses Cut in implication graph corresponds to learned clause derivable by resolution Look for small cuts – short clauses are tighter constraints

41. Leveraging Structure SAT is very hard in the worst case But practical instances often manageable Test Generation, Equivalence Checking similarity of two halves of problem Bounded Model Checking Repetitive structure Arithmetic Bit order