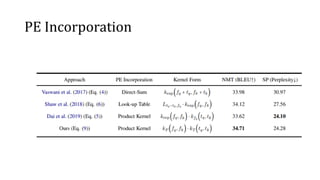
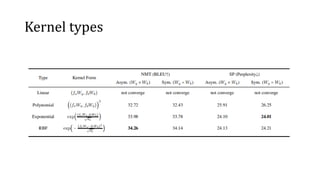
- The document presents a new formulation of the attention mechanism in Transformers using kernels. This allows defining attention over a larger space and integrating positional embeddings. - Experiments on neural machine translation and sequence prediction tasks study different kernel forms like RBF and their combination with positional encodings. - Results show the best kernel is the RBF kernel and competitive performance to state-of-the-art models with less computation.

1. Transformer Dissection: A Unified
Understanding of Transformer’s
Attention via the Lens of Kernel
Yao-Hung Hubert Tsai, Shaojie Bai, Makoto Yamada, Louis-Philippe
Morency and Ruslan Salakhutdinov
CMU, Kyoto University and RIKEN AIP
EMNLP 2019

2. Abstract
• Transformer is a powerful architecture that achieves superior
performance in NLP domain.
• Present a new formulation of attention via the lens of the kernel.
• Achieve competitive performance to the current state of the art
model with less computation in the experiments.

3. Introduction
• Transformer is a relative new architecture outperforming
traditional deep learning models such as RNN and Temporal
Convolutional Networks (TCNs) in NLP and CV domain.
• Instead of performing recurrence or convolution, Transformer
concurrently processes the entire sequence in the feed-forward
manner.

4. Introduction (cont’d)
• At the core of the Transformer is its attention mechanism, which
can be seen as a weighted combination of the input sequence,
where the weights are determined by the similarities between
elements of the input sequence.
• Be inspired to connect Transformer’s attention to kernel learning
due to the fact that they both calculate the similarity of given
sequences.

5. Introduction (cont’d)
• Develop a new variant of attention which considers a product of
symmetric kernels.
• Conduct the experiment on neural machine translation and
sequence prediction.
• Empirically study multiple kernel forms and find that the best
kernel is the RBF kernel.

6. Background

7. Linear algebra (in real number)
• Symmetric matrix
• 𝐴 = 𝐴 𝑇
• 𝐴 = 𝑄Λ𝑄−1 = 𝑄Λ𝑄 𝑇 where 𝑄 is an orthogonal matrix
• Real eigenvalues
• For 𝑚 × 𝑛 matrix 𝐴 and its transpose 𝐴⊤
, 𝐴𝐴⊤
is symmetric matrix.
• Proof: 𝐴𝐴⊤ ⊤
= 𝐴⊤ ⊤
𝐴⊤
= 𝐴𝐴⊤
• Positive-definite matrix
• Also a symmetric matrix
• All eigenvalues are positive
• All sub-determinants are positive
Source from: MIT Linear Algebra - Symmetric matrices and positive definiteness
5 2
2 3
−1 0
0 −3

8. Kernels
• A function 𝐾: 𝒳 × 𝒳 → ℝ is called a kernel over 𝒳.
• For any two points 𝑥, 𝑥′ ∈ 𝒳, 𝐾(𝑥, 𝑥′) be equal to an inner product of
vectors Φ(𝑥) and Φ(𝑥′):
∀𝑥, 𝑥′ ∈ 𝒳, 𝐾 𝑥, 𝑥′ = Φ 𝑥 , Φ 𝑥′ ,
for some mapping Φ: 𝒳 → ℍ to a *Hilbert space ℍ called a feature
space.
Source from: Foundations of Machine Learning (2 edition)
Hilbert space: vector space equipped with an inner product

9. Kernel
• A kernel 𝐾: 𝒳 × 𝒳 → ℝ is said to be positive definite symmetric
(PDS) if for any 𝑥1, … , 𝑥 𝑚 ⊆ 𝒳, the matrix 𝑲 = 𝐾 𝑥𝑖, 𝑥𝑗 𝑖𝑗
∈
ℝ 𝑚×𝑚 is symmetric positive semidefinite (SPSD).
• For a sample 𝑆 = (𝑥1, … , 𝑥 𝑚), 𝑲 = 𝐾 𝑥𝑖, 𝑥𝑗 𝑖𝑗
∈ ℝ 𝑚×𝑚 is called
the kernel matrix or the Gram matrix associated to 𝐾 and the sample S.
Source from: Foundations of Machine Learning (2 edition)

10. Kernel type
Polynomial kernels
• ∀𝑥, 𝑥′ ∈ ℝ 𝑁, 𝐾 𝑥, 𝑥′ = 𝑥 ⋅ 𝑥′ + 𝑐 𝑑
• Map the input space to a higher-dimensional space of dimension
𝑁 + 𝑑
𝑑
• Example: for an input space of dimension 𝑁 = 2 and 𝑑 = 2
• 𝐾 𝑥, 𝑥′ = 𝑥 ⋅ 𝑥′ + 𝑐 2 = 𝑥1 𝑥1
′
+ 𝑥2 𝑥2′ + 𝑐 2
• = 𝑥1
2
𝑥′
1
2
+ 𝑥2
2
𝑥′
2
2
+ 𝑐2 + 2𝑥1 𝑥1
′
𝑐 + 2𝑥2 𝑥2
′
𝑐 + 2𝑥1 𝑥1
′
𝑥2 𝑥2
′
• =〈 𝑥1
2
, 𝑥2
2
, 2𝑥1 𝑥2, 2𝑐𝑥1, 2𝑐𝑥2, 𝑐 , 𝑥′1
2
, 𝑥2
′2
, 2𝑥′1 𝑥′2, 2𝑐𝑥′1, 2𝑐𝑥′2, 𝑐 〉
Source from: Foundations of Machine Learning (2 edition)
𝑥 = 𝑥1, 𝑥2 , 𝑥′
= (𝑥1
′
, 𝑥2′)
𝑁 + 𝑑
𝑑
=
2 + 2
2
= 6

11. Kernel type (cont’d)
Gaussian kernels
• ∀𝑥, 𝑥′
∈ ℝ 𝑁
, 𝐾 𝑥, 𝑥′
= exp(−
𝑥′−𝑥
2
2𝜎2 )
• Map the input sequence to infinite number of dimensions.
• WLOG, Let 𝜎 = 1
• 𝐾 𝑥, 𝑦 = exp(
−‖𝑥−𝑦‖2
2
) = exp
− 𝑥 2− 𝑦 2
2
exp(𝑥⊤ 𝑦) = exp
− 𝑥 2− 𝑦 2
2
σ 𝑗=0
∞ 𝑥⊤ 𝑦
𝑗
𝑗!
• = exp
− 𝑥 2− 𝑦 2
2
(1 +
1
1!
𝑥⊤ 𝑦 +
1
2!
𝑥⊤ 𝑦 2 + ⋯ +
1
∞!
𝑥⊤ 𝑦 ∞)
• = exp
− 𝑥 2− 𝑦 2
2
 1,
1
1!
𝑥,
1
2!
𝑥2, … ,
1
∞!
𝑥∞ , 1,
1
1!
𝑦,
1
2!
𝑦2, … ,
1
∞!
𝑦∞ 
exp 𝑥 = ෍
𝑘=0
∞
𝑥 𝑘
𝑘!
Source from: Introduction to Machine Learning & An Intro to Kernels

12. Transformer
• Encoder-decoder model
• Different layer:
• Embedding Layer
• Positional Encoding
• Encoder/Decoder
• Output Probability Layer
Source from Attention Is All You Need and Transformer Dissection

13. Attention
• Core inside Encoder/Decoder:
• Scaled Dot-Product Attention
Attention 𝑄, 𝐾, 𝑉 = softmax
QK⊤
𝑑 𝑘
V
• Encoder-encoder attention
• Decoder-decoder attention
• Encoder-decoder attention
Source from Attention Is All You Need and Transformer Dissection

14. Multi-head attention
• Consider attention in different space
MultiHead Q, K, V = Concat head1, ⋯ , headh WO
where headi = Attention(QWi
Q
, KWi
K
, VWi
V
)
Source from Attention Is All You Need and Transformer Dissection

15. Attention

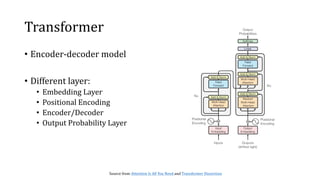
16. • Transformer’s attention is an order-agnostic operation given the
order in the inputs.
• Transformer introduced positional embedding to indicate the
positional relation for the inputs.
• 𝒙 = [𝑥1, 𝑥2, ⋯ , 𝑥 𝑇]
• 𝑥𝑖 = (𝑓𝑖, 𝑡𝑖) with
• 𝑓𝑖 ∈ ℱ non-temporal feature (E.g., word representation, frame in a video etc.)
• 𝑡𝑖 ∈ 𝒯 temporal feature (E.g., sine and cosine functions)

17. • Definition. Given a non-negative kernel function 𝑘 ⋅,⋅ : 𝒳 × 𝒳 → ℝ+
,
a set filtering function 𝑀 ⋅,⋅ : 𝒳 × 𝒮 → 𝒮, and a value function
𝑣 ⋅ : 𝒳 → 𝒴, the Attention function taking the input of a query feature
𝑥 𝑞 ∈ 𝒳 is defined as
Attention 𝑥 𝑞; 𝑀 𝑥 𝑞, 𝑆 𝑥 𝑘
= ෍
𝑥 𝑘∈𝑀 𝑥 𝑞,𝑆 𝑥 𝑘
𝑘 𝑥 𝑞, 𝑥 𝑘
σ
𝑥 𝑘
′ ∈𝑀 𝑥 𝑞,𝑆 𝑥 𝑘
𝑘 𝑥 𝑞, 𝑥 𝑘
′
𝑣(𝑥 𝑘)
• Set filtering function 𝑀 𝑥 𝑞, 𝑆 𝑥 𝑘
: 𝒳 × 𝒮 → 𝒮 returns a set with its elements
that operate with 𝑥 𝑞(E.g., mask in decoder self-attention).

18. Attention in Transformer
• Recall attention mechanism in original Transformer:
Attention 𝑥 𝑞; 𝑆 𝑥 𝑘
= softmax
𝑥 𝑞 𝑊𝑞 𝑥 𝑘 𝑊𝑘
⊤
𝑑 𝑘
𝑥 𝑘 𝑊𝑣
with 𝑥 𝑞 = 𝑓𝑞 + 𝑡 𝑞, 𝑥 𝑘 = 𝑓𝑘 + 𝑡 𝑘
• Note that the input sequences are
• same (𝑥 𝑞 = 𝑥 𝑘) for self-attention
• different (𝑥 𝑞 from decoder and 𝑥 𝑘 from encoder) for encoder-decoder attention

19. Connect to definition
• From
Attention 𝑥 𝑞; 𝑆 𝑥 𝑘
= softmax
𝑥 𝑞 𝑊𝑞 𝑥 𝑘 𝑊𝑘
⊤
𝑑 𝑘
𝑥 𝑘 𝑊𝑣
• to
Attention 𝑥 𝑞; 𝑀 𝑥 𝑞, 𝑆 𝑥 𝑘
= ෍
𝑥 𝑘∈𝑀 𝑥 𝑞,𝑆 𝑥 𝑘
𝑘 𝑥 𝑞, 𝑥 𝑘
σ
𝑥 𝑘
′ ∈𝑀 𝑥 𝑞,𝑆 𝑥 𝑘
𝑘 𝑥 𝑞, 𝑥 𝑘
′
𝑣(𝑥 𝑘)
where kernel function: 𝑘 𝑥 𝑞, 𝑥 𝑘 = exp(
𝑥 𝑞 𝑊𝑞,𝑥 𝑘 𝑊 𝑘
𝑑 𝑘
)
• 𝑣 𝑥 𝑘 = 𝑥 𝑘 𝑊𝑣
softmax 𝐱 =
exi
σ 𝑗=1
𝐾
𝑒 𝑥 𝑗

20. Set filtering function
• Set filtering function 𝑀(𝑥 𝑞, 𝑆 𝑥 𝑘
) defines how many keys and which
keys are operating with 𝑥 𝑞.
• In original Transformer
• Encoder self-attention: 𝑀 𝑥 𝑞, 𝑆 𝑥 𝑘
= 𝑆 𝑥 𝑘
• Encoder-decoder attention: 𝑀 𝑥 𝑞, 𝑆 𝑥 𝑘
= 𝑆 𝑥 𝑘
• Decoder self-attention: 𝑀 𝑥 𝑞, 𝑆 𝑥 𝑘
⊂ 𝑆 𝑥 𝑘
(due to the mask to prevent
observing future tokens)

21. Integration of positional embedding
• In original Transformer
𝑘 𝑥 𝑞, 𝑥 𝑘 ≔ 𝑘exp(𝑓𝑞 + 𝑡 𝑞, 𝑓𝑘 + 𝑡 𝑘)
• Define a larger space for composing attention
𝑘 𝑥 𝑞, 𝑥 𝑘 ≔ 𝑘 𝐹 𝑓𝑞, 𝑓𝑘 ⋅ 𝑘 𝑇 𝑡 𝑞, 𝑡 𝑘
with 𝑘 𝐹 𝑓𝑞, 𝑓𝑘 = exp(
𝑓𝑞 𝑊 𝐹,𝑓 𝑘 𝑊 𝐹
𝑑 𝑘
) and exp(
𝑡 𝑞 𝑊 𝑇,𝑡 𝑘 𝑊 𝑇
𝑑 𝑘
)
• Consider products of kernels with
• 1’st kernel measures similarity between non-temporal features
• 2’nd kernel for temporal features

22. Experiments

23. • Conduct experiments on
• Neural Machine Translation (NMT)
• Sequence Prediction (SP)
• Dataset
• IWSLT’14 German-English (De-En) dataset for NMT
• WikiText-103 dataset for SP
• Metric:
• BLEU for NMT
• Perplexity for SP

24. PE Incorporation

25. Kernel types

26. Conclusions
• Present a kernel formulation for the attention mechanism in
Transformer allowing us to define a larger space for designing
attention.
• Study different kernel forms and the ways to integrate positional
embedding on NMT and SP.