This document provides an overview of several clustering algorithms. It begins by defining clustering and its importance in data mining. It then categorizes clustering algorithms into four main types: partitional, hierarchical, grid-based, and density-based. For each type, some representative algorithms are described briefly. The document also reviews several popular clustering algorithms like k-means, CLARA, PAM, CLARANS, and BIRCH in more detail. It discusses aspects like the algorithms' time complexity, types of data handled, ability to detect clusters of different shapes, required input parameters, and advantages/disadvantages. Overall, the document aims to guide selection of suitable clustering algorithms for specific applications by surveying their key characteristics.

1. International Journal of Research in Advent Technology, Vol.2, No.6, June 2014
E-ISSN: 2321-9637
205
A Survey on Several Clustering Algorithms
1RAMAPURAM GAUTHAM, 2A.MALLIKARJUNA REDDY
1computer Science And Engineering,2computer Science And Engineering
,1agi India,2agi India
Email:1ramapuram.gautham@gmail.com,2malli42143@gmail.com
Abstract-Data mining is the process of identify patterns from large amount of information. In Data Mining,
Clustering is an important research topic and it is a unsupervised learning. Cluster analysis is one of the major data
analysis methods for clustering the large data sets. The cluster analysis deals with the problems of organization of a
Collection of data objects into clusters based on similarity. It faces many challenges such as a high dimension of the
dataset, arbitrary shapes of clusters, scalability, input parameter, domain knowledge and noisy data. Several
clustering algorithms had been proposed in the literature to address these challenges. It do not exist a single
algorithm which can meet all above requirements. This makes a great challenge for the user to do selection among
the available algorithm for the specific task. The purpose of this paper is to provide a detail overview of several
clustering algorithms, which provides guidance for the selection of suitable clustering algorithm for a specific
application.
Index Terms- data mining; clustering; clustering algorithms; partitioning methods; hierarchical methods; density
based and grid based methods;
1. INTRODUCTION
Data Mining and Data-warehousing are two branches in
the process of Knowledge Discovery in Databases
(KDD).Data mining is a process of extracting
knowledge from huge databases. Data mining uses
sophisticated mathematical algorithms to segment the
data and evaluate the probability of future events.
Cluster analysis is the one of the major task in data
mining. Clustering is unsupervised classification.
Clustering is the process of grouping the data into
classes or cluster so that objects within a cluster have
high similarity in comparison to one another, but are
very dissimilar to objects in other clusters. The objects
are clustered or grouped based on the principle of
maximizing the intra-class similarity and minimizing
the interclass similarity. . It is a main task of exploratory
data mining, and a common technique for statistical data
analysis used in many fields, including machine
earning, pattern recognition, image analysis,
information retrieval and bioinformatics. Cluster
analysis is therefore known as differently in the
different field such as a Q-analysis, typology, clumping,
numerical taxonomy, data segmentation, unsupervised
learning, data visualization, learning by
observation[10][18][9].
The clustering is more challenging task than
classification. High dimension of the dataset, arbitrary
shapes of clusters, scalability, input parameter, domain
knowledge and handling of noisy data are some of the
basic requirement cluster analysis. A large number of
algorithms had been proposed till date, each to address
some specific requirements. There do not exist a single
algorithm which can adequately handle all sorts of
requirement. This makes a great challenge for the user
to do selection among the available algorithm for the
specific task. In this paper we have provided a detailed
analytical comparison of some of the very well known
clustering algorithms
2. TYPES OF CLUSTERING METHODS
Mainly clustering algorithms are categorized into four
types: Partitional, Hierarchical, Grid and density based
algorithms.
2.1 Partitional Algorithms
The partitioning methods, in general creates k partitions
of the datasets with n objects, each partition represent a
cluster, where k<= n. It tries to divide the data into
subset or partition based on some evaluation criteria. As
checking of all possible partition is computationally
infeasible, certain greedy heuristics are used in the form
of iterative optimization [11].One such approach to
partition is based on the objective function, in which,
instead of pair-wise computations of the proximity
measures, unique cluster representatives are
constructed. Depending on how representatives are
constructed iterative partitioning algorithms are divided
into k-means and k-mediods [5] [19].The partitioning
algorithm in which each cluster is represented by the
gravity of the centre is known as k-means algorithm.

2. International Journal of Research in Advent Technology, Vol.2, No.6, June 2014
E-ISSN: 2321-9637
206
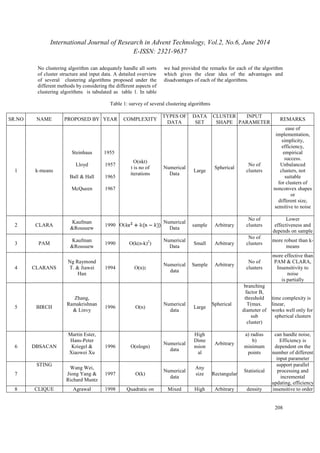
The one most efficient algorithm proposed under this
scheme is named as k-means only. The partitioning
algorithm in which cluster is represented by one of the
objects located near its centre is called as a k-mediods.
PAM, CLARA and CLARANS are three main
algorithms proposed under the k-mediod method [9].
Given D, a data set of n objects, and k, the number of
clusters to form, a partitioning algorithm organizes the
objects into k partitions (k _ n), where each partition
represents a cluster. The clusters are formed to optimize
an objective partitioning criterion, such as a
dissimilarity function based on distance, so that the
objects within a cluster are “similar,” whereas the
objects of different clusters are “dissimilar” in terms of
the data set attributes.
2.2 Hierarchical Algorithms
The hierarchical methods, in general try to decompose
the dataset of n objects into a hierarchy of a groups.
This hierarchical decomposition can be represented by a
tree structure diagram called as a dendrogram; whose
root node represents the whole dataset and each leaf
node is a single object of the dataset. The clustering
results can be obtained by cutting the dendrogram at
different level. There are two general approaches for the
hierarchical method: agglomerative (bottom-up) and
divisive (top down) [1] [9].An hierarchical
agglomerative clustering(HAC) or agglomerative
method starts with n leaf nodes(n clusters) that is by
considering each object in the dataset as a single
node(cluster) and in successive steps apply merge
operation to reach to root node, which is a cluster
containing all data objects. The merge operation is
based on the distance between two clusters. There are
three different notions of distance: single link, average
link, complete link. A hierarchical divisive clustering
(HDC) or divisive method, opposite to agglomerative,
starts with a root node that is considering all data
objects into a single cluster, and in successive steps tries
to divide the dataset until reaches to a leaf node
containing a single object. For a dataset having n
objects there is 2n-1 – 1 possible two-subset divisions,
which is very expensive in computation.
The major problem with the hierarchical methods it the
selection of merge or split points, as once done cannot
be undone. This problem also impacts the scalability of
the methods . Thus, in general hierarchical methods are
used as one of the phase in the multi phase clustering.
Different algorithms proposed based on these concepts
are: BIRCH, ROCK and Chameleon [5] [19] [9].
2.3 Grid Based Algorithms
Grid based clustering methods uses a multidimensional
grid data structure. It divides the object space into a
finite number of cells that form a grid structure on
which all of the operations for clustering are performed.
One of the distinct features of this method is the fast
processing time, as it depends not on the number of data
objects but only on the number of cells. The
representative algorithms based on this method are:
STING, WaveCluster, and CLIQUE [14].
The grid-based clustering approach uses a multire
solution grid data structure. It quantizes the object space
into a finite number of cells that form a grid structure on
which all of the operations for clustering are performed.
The main advantage of the approach is its fast
processing time, which is typically independent of the
number of data objects,
yet dependent on only the number of cells in each
dimension in the quantized space. Some typical
examples of the grid-based approach include STING,
which explores statistical information stored in the grid
cells Wave Cluster, which clusters objects using a
wavelet transform method and CLIQUE ,which
represents a grid-and density-based approach for
clustering in high-dimensional data space.
2.4 Density Based Algorithms
The density based method has been developed based on
the notion of density, which is the no of objects in the
given cluster, in this context. The general idea is to
continue growing the given cluster as long as the
density in the neighborhood exceeds some threshold;
that is for each data point within a given cluster; the
neighborhood of a given radius has to contain at least a
minimum number of points. The basic idea of density
based clustering involves a number of new definitions,
as explained below. Ε-neighborhood: the neighborhood
within a radius ε of a given object is called the ε-
neighborhood of the object. Core object: if the ε-
neighborhood of an object contains at least a minimum
number, MinPts, of objects, then the object is called a
core object. Border point: A border point has fewer than
MinPts within radius ε, but is in the neighborhood of a
core point. Directly density-reachable: given a set of
objects D, an object p is directly density -reachable
form object q if p is within the ε-neighborhood of q, and
q is a core object. (Indirectly) density-reachable: an
object p is density-reachable from object q w.r.t ε and
MinPts in a set of objects, D, if there is a chain of
objects p1,…………..pn, where p1 = p and pn = q such
that pi+1 is directly density-reachable from pi w.r.t ε
and MinPts, for 1≤i≤n.Density-connected: an object is
density - connected to object q w.r.t ε and MinPts in a
set of objects, D, if there is an object o in D such that
both p and q are density-reachable from o w.r.t ε and
MinPts. The density based algorithms can further
classified as: density based on connectivity of points
and based on density function.
The main representative algorithms in the former are

3. International Journal of Research in Advent Technology, Vol.2, No.6, June 2014
E-ISSN: 2321-9637
207
DBSCAN and its extensions, OPTICS, whereas under
the latter category are DENCLUE [5] [6] [17] [14].To
discover clusters with arbitrary shape, density-based
clustering methods have been
developed. These typically regard clusters as dense
regions of objects in the data space that are separated by
regions of low density (representing noise). DBSCAN
grows clusters according to a density-based connectivity
analysis. OPTICS extends DBSCAN to produce a
cluster ordering obtained from a wide range of
parameter settings. DENCLUE clusters objects based on
a set of density distribution functions.
3. LITERATURE REVIEW
All clustering methods basically can be categorized into
four categories: partitioning and hierarchical, based on
the properties of generated clusters [10][5]. Different
algorithms proposed may follows a good features of the
different methodology and thus it is difficult to
categorize them with the solid boundary. The detailed
categorization of the clustering algorithm is given in
[16]. The following section provides a brief review
Partitional Algorithms.
K-means is a numerical, unsupervised, non-deterministic,
iterative method. It is simple and very
fast, so in many practical applications it is proved to be
very effective in producing the good clustering results.
K-means algorithm is very sensitive in initial starting
points. K-means generates initial cluster centroids
randomly. When random initial starting points close to
the final solution, K-means has high possibility to find
out the cluster centers. Otherwise, it will lead to
incorrect clustering results.
K. A. Abdul Nazeer and et al. [3] proposed an
enhanced method to improve the accuracy and
efficiency of the K-means clustering algorithm. In this
algorithm the authors proposed two methods, one
method for finding the better initial centroids. And
another method for an efficient way for assigning data
points to appropriate clusters with reduced time
complexity. Though this algorithm produced clusters
with better accuracy and efficiency compared to k-means,
it takes O(n2) time for finding the initial
centroids.
A.Mallikarjuna reddy et al.[15] proposed an optimum
method to improve the computational complexity of K-means
algorithm with improved initial center. Though
this algorthim produces with consistent clusters
compare to the orginal K-means, it takes O(nlogn) time
for finding the intial centroids.
Koheri Arai et al. [13] proposed an algorithm for
centroids initialization for K-means. In this algorithm
both K-means and hierarchical algorithms are included.
First, in this algorithm K-means is applied many times
and each maintains centroids in the data set C. Next,
the data set C is giving as an input to the hierarchical
clustering algorithm. The hierarchical clustering
algorithm runs until it gets the desired number of
clusters. After that, calculate mean of each cluster, these
means will be the initial centroids. This algorithm gives
the better initial centroids. But in this algorithm K-means
is applied many times, so it is computationally
expensive in the presence of large data sets.
Fahim A.M et al. proposed an enhanced method
for assigning data points to clusters. The original K-means
algorithm is computationally expensive because
each iteration computes the distances between data
points and all centroids. Fahim approach makes use of
an effective method to reduce the complexity. But this
method presumes that the initial centroids are
determined randomly, as in the case of the original K-means
algorithm. Hence there is no guarantee for the
quality of the final clusters which depends solely on the
selection of initial centroids.
Fang Yuan et al. [8] proposed a systematic method
for finding the initial centroids. The centroids obtained
by this method will be consistent with the distribution of
data and hence produced better clustering. However,
Yuans method does not suggest any improvement to the
time complexity of the K-means algorithm.
Bhattacharya et al.[4] proposed a novel clustering
algorithm, called Divisive Correlation Clustering
Algorithm (DCCA) for grouping of genes. DCCA is
able to produce clusters, without taking the initial
centroids and the value of k, the number of desired
clusters as an input. The time complexity of the
algorithm is high and the cost for repairing from any
misplacement is also high.
Zhang chen et al.[7] proposed the initial
centroids algorithm that avoids the random selection of
initial centroids in k-means algorithm.
K. A. Abdul Nazeer and et al. [2] proposed an
enhanced method to improve the time complexcity of k-means.
4. SUREVEY ON SEVERAL CLUSTERING
ALGORITHMS
The clustering is more challenging task than
classification. Large number of algorithms had been
proposed till date, each to solve some specific issues.

4. International Journal of Research in Advent Technology, Vol.2, No.6, June 2014
E-ISSN: 2321-9637
208
No clustering algorithm can adequately handle all sorts
of cluster structure and input data. A detailed overview
of several clustering algorithms proposed under the
different methods by considering the different aspects of
clustering algorithms is tabulated as table 1. In table
we had provided the remarks for each of the algorithm
which gives the clear idea of the advantages and
disadvantages of each of the algorithms.
Table 1: survey of several clustering algorithms
SR.NO NAME PROPOSED BY YEAR COMPLEXITY
TYPES OF
DATA
DATA
SET
CLUSTER
SHAPE
INPUT
PARAMETER
REMARKS
1 k-means
Steinhaus
Lloyd
Ball & Hall
McQueen
1955
1957
1965
1967
O(nkt)
t is no of
iterations
Numerical
Data
Large
Spherical
No of
clusters
ease of
implementation,
simplicity,
efficiency,
empirical
success.
Unbalanced
clusters, not
suitable
for clusters of
nonconvex shapes
or
different size,
sensitive to noise
2 CLARA
Kaufman
&Rousuew
1990 O( Numerical
Data
sample Arbitrary
No of
clusters
Lower
effectiveness and
depends on sample
3 PAM
Kaufman
&Rousuew
1990 O(k(n-k)2)
Numerical
Data
Small Arbitrary
No of
clusters
more robust than k-means
4 CLARANS
Ng Raymond
T. & Jiawei
Han
1994 O(n)2
Numerical
data
Sample Arbitrary
No of
clusters
more effective than
PAM & CLARA,
Insensitivity to
noise
is partially
5 BIRCH
Zhang,
Ramakrishnan
& Linvy
1996 O(n)
Numerical
data
Large
Spherical
branching
factor B,
threshold
T(max.
diameter of
sub
cluster)
time complexity is
linear,
works well only for
spherical clusters
6 DBSACAN
Martin Ester,
Hans-Peter
Kriegel &
Xiaowei Xu
1996 O(nlogn)
Numerical
data
High
Dime
nsion
al
Arbitrary
a) radius
b)
minimum
points
can handle noise,
Efficiency is
dependent on the
number of different
input parameter
7
STING
Wang Wei,
Jiong Yang &
Richard Muntz
1997 O(k)
Numerical
data
Any
size Rectangular
Statistical
support parallel
processing and
incremental
updating, efficiency
8 CLIQUE Agrawal 1998 Quadratic on Mixed High Arbitrary density insensitive to order

5. International Journal of Research in Advent Technology, Vol.2, No.6, June 2014
E-ISSN: 2321-9637
209
Rakesh,
Johannes
Gehrke,
Dimitrios
Gunopulos &
Prahhakar
Raghavan
# of
dimensions
data Dime
nsion
al
threshold of input
scales well. Results
are highly
dependent on the
input parameter
9
DENCLUE
Hinneburg &
Keim 1998 O(n2)
Numerical
data
High
Dime
nsion
al
Arbitrary
density
parameter,
noise
threshold
good
clustering
properties
with large amt of
noisy data set,
compact
representation of
clusters
10
WAVE
CLUSTER
Sheikholeslami
,
Gholamhosein,
Surojit
Chatterjee &
Aidong Zhang
1998
O(n)
Numerical
data
Large Arbitrary
No
outperforms
BIRCH,
CLARANS
& DBSCAN in
terms
of both efficiency
and clustering
quality, capable of
handling data with
up to 20
dimensions
11
CHAMELE
ON
Karypis 1999 O(n2)
Discrete
data
Small
Arbitrary Min.
Similarity
high quality
clusters
12
OPTICS
Ankerst 1999 O(nlogn)
Numerical
data
High
Dime
nsion
al
Arbitrary
density
threshold
No need for input
parameter settings
& Can not handle
clusters of different
densities
13
ROCK
Guha Sudipto,
Rajeev Rastogi
& Kyuseok
Shim
1999 O(n2)
Categorical
Data
Small
Graph
similarity
threshold
based on HAC
& more powerful
than
traditional
hierarchical
clustering
14 MAFIA
Sanjay Goil,
Harsha Nagesh
and Alok
1999
O(ck’+N/pBk’γ+
αSpk’)
Numerical
data
Moderate Arbitrary
No. of
dimensions
40 to 50 times
faster than
CLIQUE
15 CURE
Sudipto Guha,
Rajeev Rastogi
Kyuseok Shim
2001 O( Numerical
data
Moderate
Or
Small
Spherical
No.of points
Or
Datapoints
Do not handle for
large databases
16 K-means++
David Arthur
and Sergei
2007 O(log k)
Numerical
data
Large Spherical No of clusters The initial cluster
centers according

6. International Journal of Research in Advent Technology, Vol.2, No.6, June 2014
E-ISSN: 2321-9637
Vassilvitskii to metric and
not informing at
random.
Lower potential
than k-means
210
5. CONCLUSION
Cluster analysis is the one of the major task in data
mining. Clustering is unsupervised classification.
Clustering is the process of grouping the data into
classes or cluster so that objects within a cluster have
high similarity in comparison to one another, but are
very dissimilar to objects in other clusters. The
objects are clustered or grouped based on the
principle of maximizing the intra-class similarity and
minimizing the interclass similarity. It is a main task
of exploratory data mining, and a common technique
for statistical data analysis used in many fields,
including machine learning, pattern recognition,
image analysis, information retrieval and
bioinformatics. In the literature several number of
clustering algorithms had been proposed which
satisfy certain criteria such as arbitrary shapes, high
dimensional database, and domain knowledge. It had
been also proved that it is not possible to design a
single clustering algorithm which fulfils all the
requirement of clustering. Therefore it is very
difficult to select any algorithm for a specific
application. In this paper we did survey on several
clustering algorithms and also provided merits and
demerits on each algorithm which makes the
selection process easier for the user.
REFERENCES
[1]Abbas.O.A, ―Comparisons between Data
Clustering Algorithmsǁ, The Int. Journal of Info.
Tech. ,vol. 5, pp . 320-325,Jul.2008.
[2]AbdulNazeer.K.A, MadhuKumar SD,
Sebastian.M.P. 2011. Enhancing the K-means
Clustering Algorithm by Using a O(nlogn)
Heuristic Method for Finding Better Initial
Centroids. International Conference on Emerging
Applications of Information Technology- EAIT
2011. , Calcutta, India: IEEE Computer Society.
[3]Abdul Nazeer.K.A and M. P. Sebastian,
Improving the accuracy and efficiency of the k-means
clustering algorithm,"in International
Conference on Data Mining and Knowledge
Engineering (ICDMKE), Proceedings of the
World Congress on Engineering (WCE-2009),
Vol I, July 1-3, 2009, London,U.K.
[4]Bhattacharya and R. K. De, “Divisive Correlation
Clustering Algorithm (DCCA) for grouping of
genes:detecting varying patterns in expression
profiles,bioinformatics, Vol. 24, pp. 13591366,
2008.
[5]Berkhin.P (2001) ―Survey of Clustering Data
17
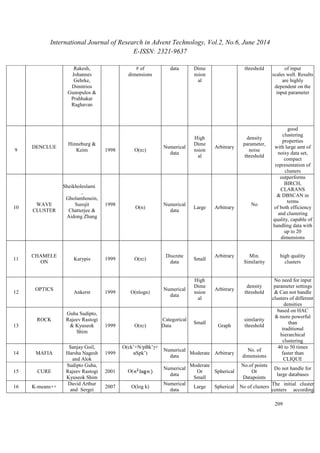
AFFINTY
PROPOGATION
Inmar Givoni
, Clement
Chung,
Brendan J. Frey
2007 O( Numerical
data
Moderate Arbitrary Data points
The sum of changes
of all messages in
one iteration is
smaller than a
thresholds.
18 E2 k-means AbdulNazeer.K.A 2007 O(n)2 Numerical
data Moderate Arbitrary
No of
clusters
High in time
complexity
19
HEURISTIC k-means
AbdulNazeer.K.A 2011
O(nlogn)
Numerical
data
Moderate
or small
Arbitrary
No of
clusters
Better initial
centroids will be
obtained
20
ENHANCED K-Means
Bangoria Bhoomi
M. 2014 O(pk)
Numerical
Data Moderate
Arbitrary
No of
clusters
Same as the
heuristic but differs
with selection of
centers
21
OPTIMUM
METHOD
A.Mallikarjuna
reddy,R.
Gautham 2014
O(nlogn)
Numerical
data Large
Arbitrary
No of
clusters
Reduced time
complexcity of K-means
with
improved initial
centers

7. International Journal of Research in Advent Technology, Vol.2, No.6, June 2014
E-ISSN: 2321-9637
211
MiningTechniquesǁ[Online].Available:
http://www.accure.com/products/rpcluster_review
.pdf.
[6]Dr.Chandra.E, V. P. Anuradha, ― A Survey
on Clustering Algorithms for Data in Spatial
Database Management Systems, International
Journal of Computer Application, vol. 24, pp . 19-
26.
[7] Chen Zhang and Shixiong Xia, “ Kmeans
Clustering Algorithm with Improved Initial
center,” in Second International Workshop on
Knowledge Discovery and Data Mining (WKDD),
pp. 790792, 2009.
[8] Fang Yuan , Zeng-Hui-Meng , Hong-Xia Zhangz
and Chun-Ru Dong ,A New Algrothim to Get the
Initial Centroids,"Department of Computer
Science, Baoding College of Finance, Baoding,
071002 P.R.China, IEEE Aug 2004
[9]Han.J , M. Kamber, Data Mining, Morgan
Kaufmann Publishers, 2001.
[10]Jain.A.K, M . N. M urty, P. J. Flynn―Data
Clustering: A Review, ACM Computing Surveys,
vol. 31, pp . 264-323, Sep . 1999.
[11]Jain.A.K, ―Data Clustering: 50 Years Beyond
K-M eans, in Pattern Recognition Letters, vol. 31
(8), pp . 651-666, 2010.
[12]Kelinberg.J, ―An impossibility theorem for
clustering, in NIPS 15, M IT Press,2002, p p .
446-453.
[13]Koheri Arai and Ali Ridho Barakbah
,Hirerachical K-means: An algorithm for
Centroids intialization for k-means,"Reports of
the Faculty of Science and Engineering, Saga
University, Vol. 36, No.1, 2007.
[14]Kotsiantis.S.B, P. E. Pintelas, ―Recent
Advances in Clustering: A Brief Survey ǁ WSEAS
Transactions on Information Science and
Applications, Vol. 1, No. 1, pp. 73–81, Citeseer,
2004.
[15]Mallikarjuna Reddy.A and R.Gautham: An
Optimum method for enhancing the
computational complexity of k-means clustering
algorithm with improved initial centers “IJSR in
Volume 3 Issue 6, June 2014.
[16] Neha Soni, Amit Ganatra, ―Categorization of
Several Clustering Algorithms from Different
Perspective: A Reviewǁ, International Journal of
Advanced Research in Computer Science and
Software Engineering, vol. 2, no. 8, pp. 63-68,
Aug. 2012.
[17]Rama. B, P. Jay ashree, S. Jiwani, ― A Survey
onclustering Current status and challenging
issues,International Journal of Computer Science
andEngineering, vol. 2, pp. 2976-2980.
[18]Ravichandra Rao.I.K, Data Mining and
Clustering Techniquesǁ, DRTC Workshop on
Semantic Web,Bangalore, 2003.
[19] Rui Xu, Donald C. Wunsch II, ―Survey of
Clustering Algorithmsǁ, IEEE Transactions on
neural Networks, vol. 16, pp. 645-678, May 2005.