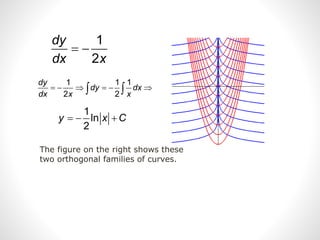
This document discusses orthogonal trajectories and provides examples of finding orthogonal trajectories for different families of curves. It begins by defining orthogonal trajectories as curves that intersect each other at right angles. It then provides a method for finding the differential equation that describes the orthogonal trajectories for a given family of curves. Several examples are worked out, such as finding the orthogonal trajectories of the family of parabolas with equation y = x^2. Applications to equipotential lines and electric fields and electromagnetic waves are also mentioned.

1. Names of group members
1. Syed Umar Rasheed (14093122-002)
2. Adnan Aslam (14093122-003)
3. Bilal Amjad (14093122-004)
4. Inzmam Tahir (14093122-005)

2. Orthogonal Trajectories
in rectangular coordinate
system

3. Definition
• An orthogonal trajectory of a family of curves is a curve
that intersects each curve of the family orthogonally—
that is, at right angles.

4. Suppose that we have a family of curves given by
and another family of curves
𝑔 𝑥, 𝑦 = 0
such that at any intersection of the curves of the first
family with a curve of the second family, the tangents of
the curves are perpendicular.
Orthogonal trajectories, therefore, are two families of
curves that always intersect perpendicularly.
𝑓 𝑥, 𝑦 = 0

5. Let us consider the example of the two families
𝑦 = 𝑚𝑥 𝑎𝑛𝑑 𝑦2 + 𝑥2 = 𝑐2
If we draw the two families together on the same graph
we get

6. METHOD
( , )
dy
f x y
dx

1
( , )
dy
dx f x y
 
Find the differential equation for the given family of
curves, by differentiating
Find the differential equation of the Orthogonal
Trajectory
Separating variables and integrating the above differential
equation we get the algebraic equation of the family of
orthogonal trajectories.
Given family of curve 𝑓 𝑥, 𝑦 = 0
STEP 1
STEP 2
STEP 3
𝑑𝑥
𝑑𝑦
= −𝑓( 𝑥, 𝑦)or

7. Orthogonal Curves
2
Consider the family of parabola . Find the family of curves
which intersect the above family of parabola perpendicularly.
y x C 
Example
Solution
Two curve intersect perpendicularly if the product of the slopes of
the tangents at the intersection point is -1.
The differential equation for the orthogonal family of curves.
𝑑𝑦
𝑑𝑥
= −
1
2𝑥
By differentiation we get
𝑑𝑦
𝑑𝑥
= 2𝑥 . Hence the family of
parabola in question satisfies the differential equation
𝑑𝑦
𝑑𝑥
= 2𝑥.

8.       
1 1 1
2 2
dy
dy dx
dx x x
The figure on the right shows these
two orthogonal families of curves.
 
1
2
dy
dx x
  
1
ln
2
y x C

9. Example Find the orthogonal trajectories of all parabolas with vertices at
the origin and foci on the x-axis
𝒚 𝟐
= 𝟒𝒂𝒙
𝒚 𝟐
𝒙
= 𝟒𝒂
STEP 1: Differentiate Eq 1
Eq 1
𝒙
𝒅
𝒅𝒙
𝒚 𝟐
− 𝒚 𝟐 𝒅
𝒅𝒙
(𝒙)
𝒙 𝟐
= 𝟎
𝟐𝒙𝒚
𝒅𝒚
𝒅𝒙
− 𝒚 𝟐
= 𝟎
𝒅𝒚
𝒅𝒙
=
𝒚
𝟐𝒙
STEP 2: Differential equation of the orthogonal trajectories
𝒅𝒚
𝒅𝒙
= −
𝟐𝒙
𝒚

10. STEP 3: Solving the differential equation by method of separation of variables
𝒅𝒚
𝒅𝒙
= −
𝟐𝒙
𝒚
−𝒚𝒅𝒚 = 𝟐𝒙𝒅𝒙
∫ 𝟐𝒙 𝒅𝒙 + ∫ 𝒚𝒅𝒚 = ∫ 𝟎 ,integrating both sides
𝒙 𝟐 +
𝒚 𝟐
𝟐
= 𝑪
𝟐𝒙 𝟐 + 𝒚 𝟐 = 𝑪
𝟐𝒙 𝟐 + 𝒚 𝟐 = 𝒃 𝟐

11. Exercise 9.7
Find the orthogonal trajectories of each of the
following.
1) 𝑥2
− 𝑦2
= 𝑐
2) 𝑥 = 𝑐𝑦2
3) 𝑥2
+ 𝑦2
= 𝑐𝑥
4) 𝑦 = 𝑒 𝑐𝑥
5) 𝑦 = 𝑥 − 1 + 𝑐𝑒−𝑥

12. Applications
• Equipotential Lines and Electric Fields

13. • Electromagnetic waves consist of both electric and magnetic
field waves. These waves oscillate in perpendicular planes with
respect to each other.

14. • The light rays of sun that passes through the
orbits of the planets.

15. References
• www.slideshare.com
• www.quora.com
• www.mathcity.com
• www.wikipedia.com