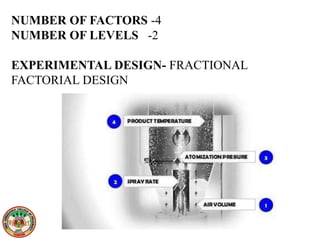
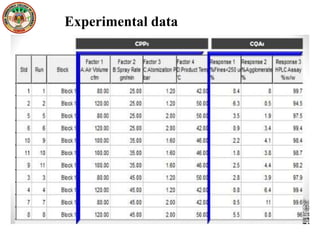
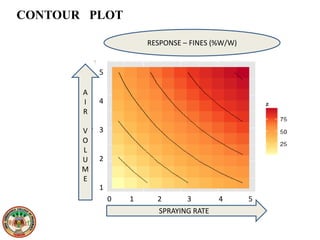
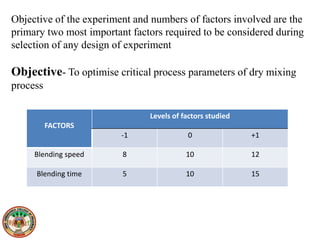
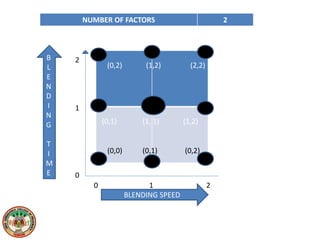
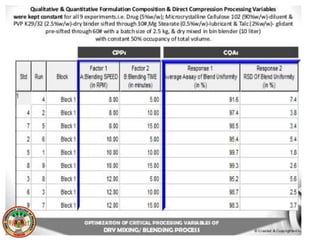
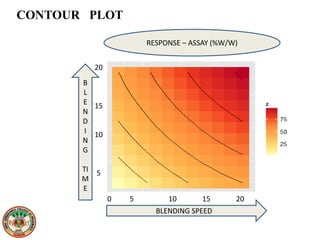
This document discusses various design of experiment methodologies including screening designs and optimization designs. It provides examples of factorial designs, response surface designs like central composite designs and Box-Behnken designs, and three-level full factorial designs. It also gives an example of using a fractional factorial design to screen critical processing parameters in a wet granulation coating process and selecting a three-level full factorial design to optimize two factors, blending speed and time, in a dry mixing process to investigate their interactive and quadratic effects on the response.

1. Department of Pharmaceutics
SREE SIDDAGANGA COLLEGE OF PHARMACY
Optimization Technology And Screening
Design
By:
SATHISH H T
2nd Sem M Pharm

2. Completely randomized designs
Randomized block designs
Factorial designs
Full
Fractional
Response surface designs
Central composite designs
Box-Behnken designs
Three level full factorial designs
Types of screening designs….

3. Completely randomized Designs
 These designs compares the values of a response variable based
on different levels of that primary factor
 For example ,if there are 3 levels of the primary factor with each
level to be run 2 times then there are 6 factorial possible run
sequences.
Randomized block designs
For this there is one factor or variable that is of primary interest.
To control non-significant factors, an important technique called
blocking can be used to reduce or eliminate the contribution of these
factors to experimental error.

4. Factorial Design
These are the designs of choice for simultaneous determination of the
effects of several factors & their interactions.
Symbols to denote levels are:
when both the variables are in low concentration.
• a- one low variable and second high variable.
• b- one high variable and second low variable
• ab- both variables are high.
 Factorial designs are optimal to determined the effect of pressure
& lubricant on the hardness of a tablet
 Effect of disintegrant & lubricant conc . on tablet dissolution .
 It is based on theory of probability and test of significance.

5. Response surface designs
This model has quadratic form
Designs for fitting these types of models are known as response
surface designs.
If defects and yield are the outputs and the goal is to minimize
defects and maximize yield

6. Two most common designs generally used in this response surface
modeling are
Central composite designs
Box-Behnken designs
Box-Wilson central composite Design
This type contains an embedded factorial or fractional factorial
design with centre points that is augmented with the group of ‘star
points’.
These always contains twice as many star points as there are factors
in the design

7. The star points represent new extreme value (low & high) for
each factor in the design
To picture central composite design, it must imagined that there
are several factors that can vary between low and high values.
Central composite designs are of three types
Circumscribed(CCC) designs-Cube points at the corners of the
unit cube, star points along the axes at or outside the cube and
centre point at origin
Inscribed (CCI) designs-Star points take the value of +1 & -1
and cube points lie in the interior of the cube
Faced(CCF) –star points on the faces of the cube.

8. Box-Behnken design
Box-Behnken designs use just three levels of each factor.
In this design the treatment combinations are at the midpoints of
edges of the process space and at the center. These designs are
rotatable (or near rotatable) and require 3 levels of each factor
These designs for three factors with circled point appearing at the
origin and possibly repeated for several runs. It’s alternative to CCD.
The design should be sufficient to fit a quadratic model , that justify
equations based on square term & products of factors.

9. Three-level full factorial designs
It is written as 3k factorial design.
It means that k factors are considered each at 3 levels.
These are usually referred to as low, intermediate & high values.
These values are usually expressed as 0, 1 & 2
The third level for a continuous factor facilitates investigation of
a quadratic relationship between the response and each of the
factors

10. SCREENING & OPTIMIZATION OF CPPs OF
WURSTER COATING DRUG LAYERING
PROCESS

11. NUMBER OF FACTORS -4
NUMBER OF LEVELS -2
EXPERIMENTAL DESIGN- FRACTIONAL
FACTORIAL DESIGN

13. Experimental data

14. CONTOUR PLOT
0
0
0
0
5
4
3
2
1
000 1 2 3 4 5
A
I
R
V
O
L
U
M
E
SPRAYING RATE
RESPONSE – FINES (%W/W)

15. 3D PLOT
F
I
N
E
S

17. Objective of the experiment and numbers of factors involved are the
primary two most important factors required to be considered during
selection of any design of experiment
Objective- To optimise critical process parameters of dry mixing
process
FACTORS
Levels of factors studied
-1 0 +1
Blending speed 8 10 12
Blending time 5 10 15

18. BLENDING SPEED
B
L
E
N
D
I
N
G
T
I
M
E
0 1 2
2
1
0
NUMBER OF FACTORS 2
(0,2) (1,2) (2,2)
(0,1) (1, 1) (1,2)
(0,0) (0,1) (0,2)

19. In Dry Mixing Process, 2 Processing Parameters were
critical & required to be optimized
 Moreover, It was required to investigate interactive
& quadratic relationship between factors & response to
find out optimum ranges
 Thus, 3 Level FFD is a time & cost effective best
option for optimization of 2 factors.
 However 3 Level FFD facilitates investigation of
interactive & quadratic relationship of factors &
response.
EXPERIMENTAL DESIGN SELECTED
3 LEVEL FULL FACTORIAL DESIGN

21. CONTOUR PLOT
00
00
20
15
10
5
000 5 10 15 20
B
L
E
N
D
I
N
G
TI
M
E
BLENDING SPEED
RESPONSE – ASSAY (%W/W)

22. ANY QUESTIONS ?

23. THANK YOU