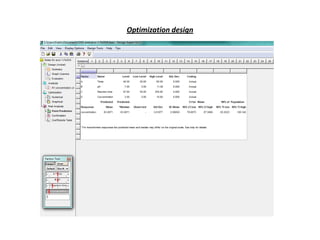
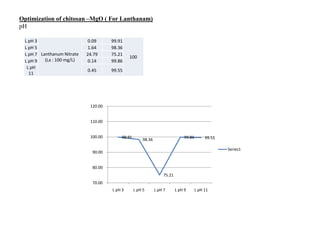
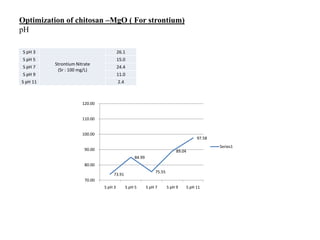
This document describes a study that used response surface methodology (RSM) to optimize the removal of lanthanum metal from wastewater using chitosan-Fe3O4 nanocomposite as an adsorbent. Four variables (adsorbent dose, temperature, pH, and reaction time) were investigated using a Box-Behnken experimental design. Regression analysis identified pH as the most significant factor. Optimization analysis predicted that the maximum lanthanum removal of 91.82% could be achieved at 25.41°C, pH 10.24, 150 minutes reaction time, and 6.5 mg/L lanthanum concentration. A similar RSM study optimized removal of strontium using chitos

1. Magnetite (Chitosan-Fe3O4.
) nanocomposite for removal of heavy metals
from aqueous solutions
Objective :
To optimize (RSM) removal of lanthanum metal from waste water using Chitosan-Fe3O4.
RSM
Response surface modeling (RSM) is an empirical statistical technique that uses quantitative data obtained from
appropriately designed experiments to determine regression model and operating conditions (Alam et al., 2007;
Ricou-Hoeffer et al., 2001; Tan et al., 2008).
Optimization studies : Four variables
Adsorbent dose
Temperature
pH of the solution
Reaction time

2. Box–Behnken design
Due to its Suitability to fit quadratic surface
• 28 experiments were formulated
• The optimum values of the selected variables were obtained
by solving the regression equation
• Each of the parameters was coded at Maximum and minimum
The chosen independent variables used in this study were coded
according to Equation
• xi is the dimensionless coded value
• X0 is the value of Xi at the center point and ∆X is the step change value
The behavior of the system is explained by the following empirical second-order polynomial
model Eq

3. Variables
Adsorbent dose – 3mg to 10mg
Temperature - 20̊ C to 60̊ C
pH of the solution- 3 to 11
Reaction time -10min to 250min

4. Calculating the experimental points
Design-Expert?Software
Factor Coding: Actual
Std Error of Design
Std Error Shading
1.500
0.500
X1 = A: Temp
X2 = B: pH
Actual Factors
C: Reaction time = 214.865
D: Concentration = 8.67568
20 30 40 50 60
3
5
7
9
11
Std Error of Design
A: Temp (cel)
B:pH
0.5
0.6
0.7
0.8 0.8
0.8 0.8
0.9 0.9
0.9 0.9
1 1

5. Design-Expert?Software
concentration
Color points by value of
concentration:
99.88
74.73
Run Number
ExternallyStudentizedResiduals
Residuals vs. Run
-6.00
-4.00
-2.00
0.00
2.00
4.00
1 5 9 13 17 21 25 29

6. Effects Half-Normal Probability Plot
• Large effects (absolute values) appear in the upper-right section of the plot.
• The lower-left portion of the plot contains effects caused by noise rather than a true effect
Design-Expert?Software
concentration
Color points by value of
concentration:
99.88
74.73
Actual
Predicted
Predicted vs. Actual
70
80
90
100
110
70 80 90 100 110

7. Perturbation
It comprises mathematical methods for finding an approximate solution to a problem
It helps to compare the effect of all the factors at a particular point in the design space
Design-Expert?Software
Factor Coding: Actual
Std Error of Design
Actual Factors
A: Temp = 30.2703
B: pH = 3.64865
C: Reaction time = 214.865
D: Concentration = 8.67568
-2.000 -1.000 0.000 1.000 2.000
0.400
0.600
0.800
1.000
1.200
1.400
1.600
A A
B B
C C
D D
Perturbation
Deviation from Reference Point (Coded Units)
StdErrorofDesign

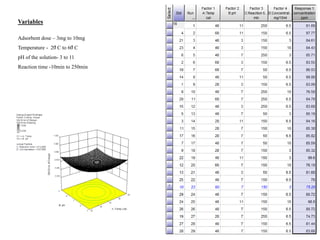
8. ANOVA for Response Surface Quadratic model
Analysis of variance table [Partial sum of squares - Type III]
Sum of Mean F p-value
Source Squares df Square Value Prob > F
Model 1201.79 14 85.84 6.58 0.0006 significant
A-Temp 2.00 1 2.00 0.15 0.7011
B-pH 544.86 1 544.86 41.79 < 0.0001
C-Reaction time 60.84 1 60.84 4.67 0.0486
D-Concentration 6.37 1 6.37 0.49 0.4962
AB 2.48 1 2.48 0.19 0.6693
AC 24.21 1 24.21 1.86 0.1945
AD 0.18 1 0.18 0.014 0.9080
BC 25.96 1 25.96 1.99 0.1801
BD 0.096 1 0.096 7.371E-003 0.9328
CD 22.71 1 22.71 1.74 0.2081
A^2 0.20 1 0.20 0.015 0.9039
B^2 488.78 1 488.78 37.49 < 0.0001
C^2 6.27 1 6.27 0.48 0.4994
D^2 8.55 1 8.55 0.66 0.4316
Residual 182.53 14 13.04
Lack of Fit 166.03 10 16.60 4.03 0.0958 not significant
Pure Error 16.49 4 4.12
Cor Total 1384.32 28
The Model F-value of 6.58 implies the model is significant. There is only
a 0.06% chance that an F-value this large could occur due to noise.

9. Design-Expert?Software
Factor Coding: Actual
Desirability
X1 = A: Temp
X2 = B: pH
X3 = C: Reaction time
Actual Factor
D: Concentration = 10
Cube
Desirability
A: Temp (cel)
B:pH
C: Reaction time (min)
A-: 20 A+: 60
B-: 3
B+: 11
C-: 50
C+: 250
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1.000
Prediction 1

10. A:Temp = 40
20 60
B:pH = 7
3 11
C:Reaction time = 50
50 250
D:Concentration = 3
3 10
Desirability = 1.000

11. The 3D Surface plot is a projection of the contour plot
Design-Expert?Software
Factor Coding: Actual
concentration (ppm)
Design points above predicted value
25.27
0.12
X1 = B: pH
X2 = C: Reaction time
Actual Factors
A: Temp = 20
D: Concentration = 6.5
50
100
150
200
250
3
5
7
9
11
-10
0
10
20
30
concentration(ppm)
B: pHC: Reaction time (min)
Design-Expert?Software
Factor Coding: Actual
concentration (ppm)
Design points above predicted value
Design points below predicted value
25.27
0.12
X1 = A: Temp
X2 = B: pH
Actual Factors
C: Reaction time = 250
D: Concentration = 6.5
3
5
7
9
11
20
30
40
50
60
0
5
10
15
20
25
30
concentration(ppm)
A: Temp (cel)B: pH
Design-Expert?Software
Factor Coding: Actual
concentration (ppm)
Design points above predicted value
Design points below predicted value
25.27
0.12
X1 = A: Temp
X2 = C: Reaction time
Actual Factors
B: pH = 7
D: Concentration = 6.5
50
100
150
200
250
20
30
40
50
60
0
5
10
15
20
25
30
concentration(ppm)
A: Temp (cel)C: Reaction time (min)

12. Optimization design

13. Temp 25.41
pH 10.24
Reaction time 150.00
Concentration 6.50
Mean
91.8215
The equilibrium adsorption capacity was calculated from the
relationship
=((10-0.13mg/lt *1lt)/3mg
=9.7mg/3mg

14. Optimization of chitosan –MgO ( For Lanthanam)
pH
L pH 3
Lanthanum Nitrate
(La : 100 mg/L)
0.09 99.91
100
L pH 5 1.64 98.36
L pH 7 24.79 75.21
L pH 9 0.14 99.86
L pH
11
0.45 99.55
99.91
98.36
75.21
99.86 99.55
70.00
80.00
90.00
100.00
110.00
120.00
L pH 3 L pH 5 L pH 7 L pH 9 L pH 11
Series1

15. S pH 3
Strontium Nitrate
(Sr : 100 mg/L)
26.1
S pH 5 15.0
S pH 7 24.4
S pH 9 11.0
S pH 11 2.4
Optimization of chitosan –MgO ( For strontium)
pH
73.91
84.99
75.55
89.04
97.58
70.00
80.00
90.00
100.00
110.00
120.00
S pH 3 S pH 5 S pH 7 S pH 9 S pH 11
Series1