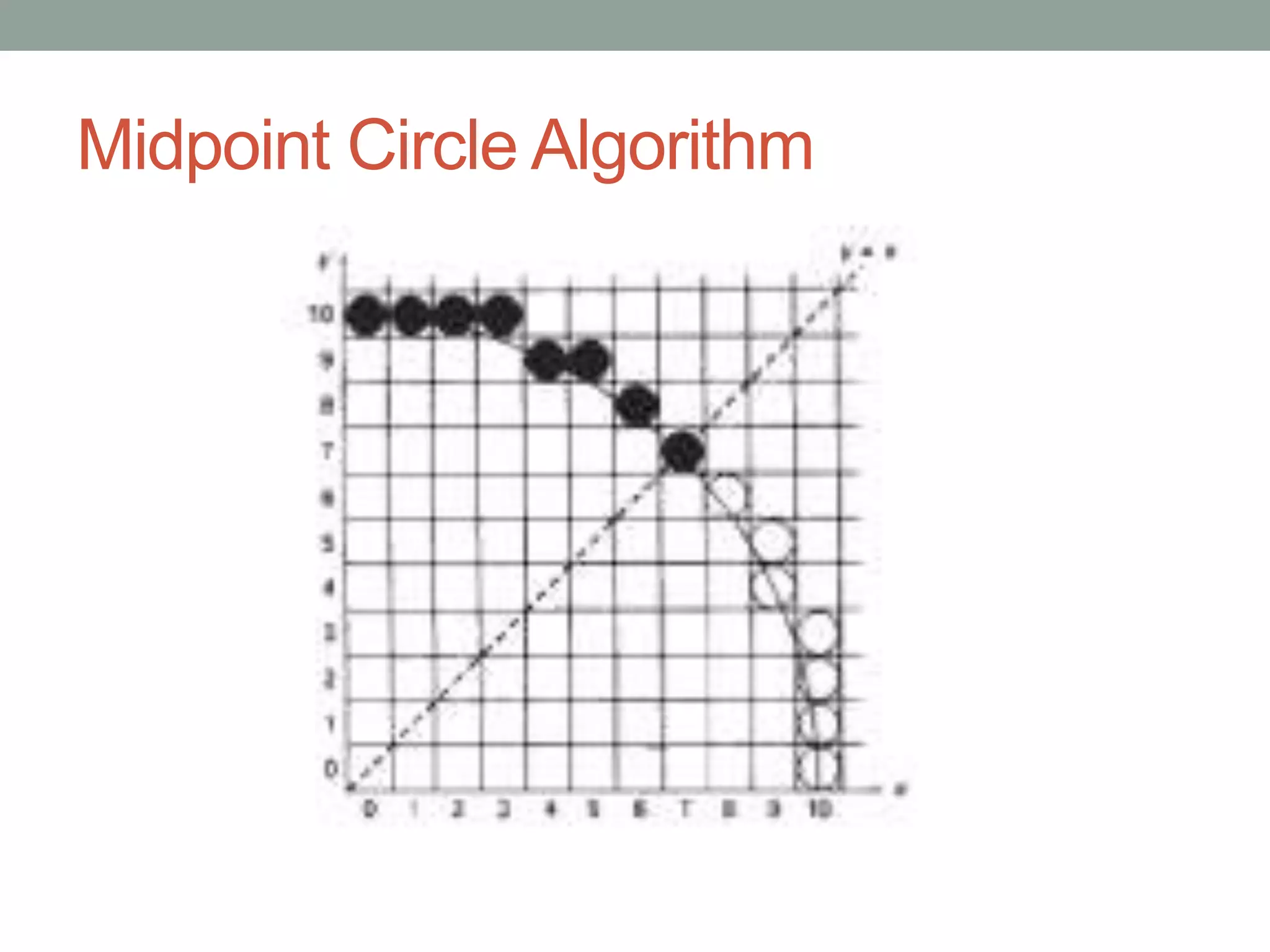
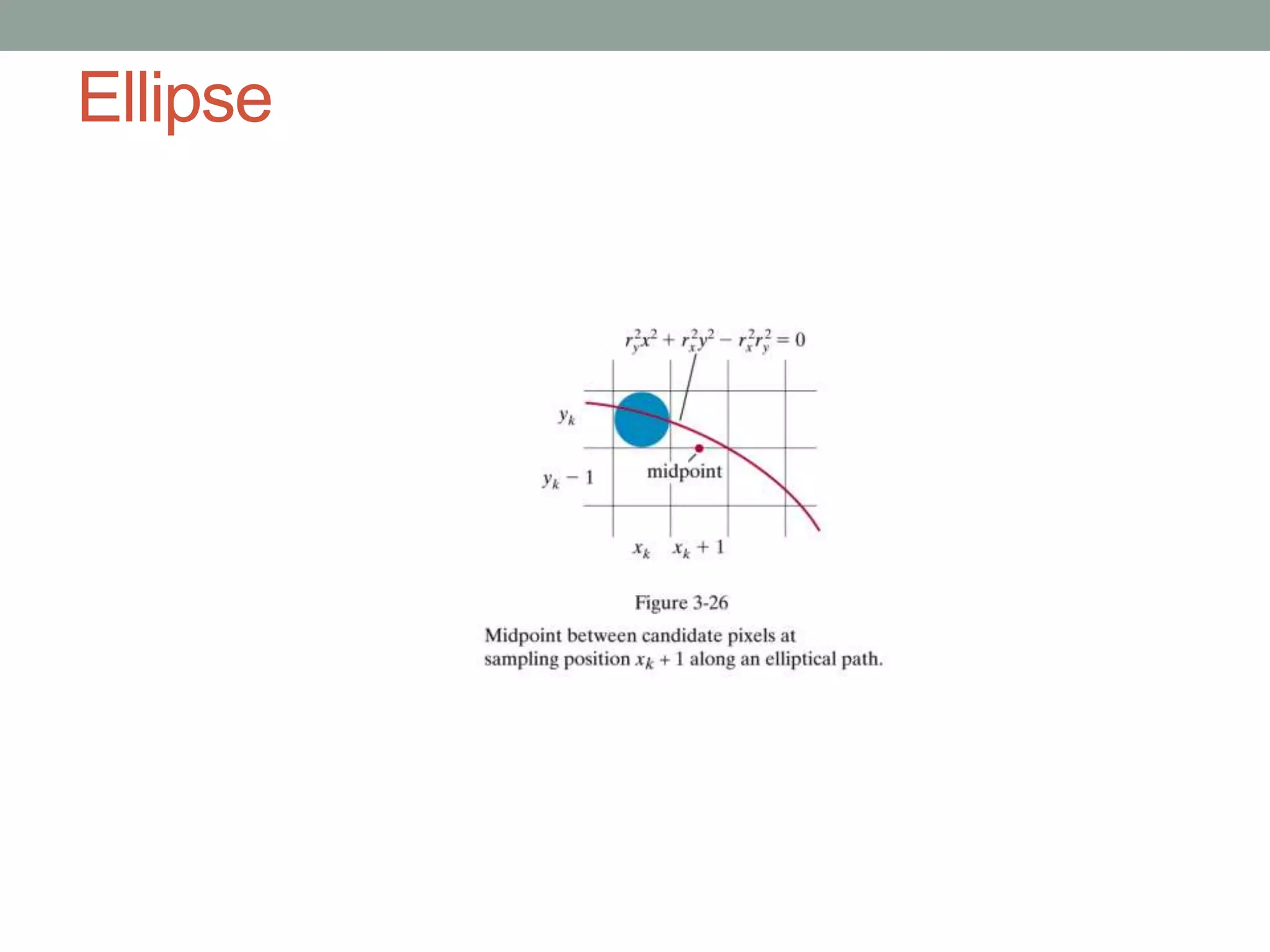
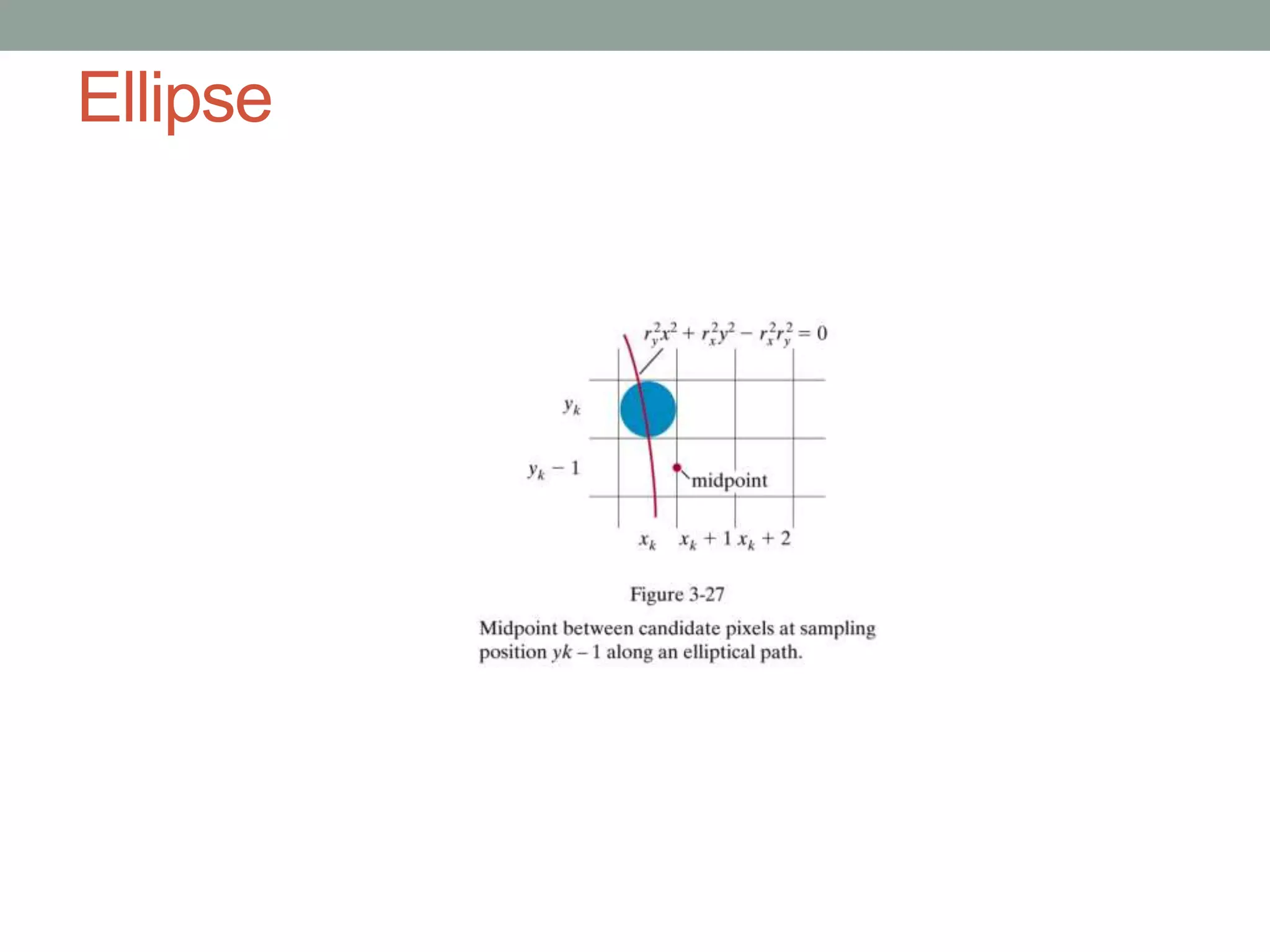
This document discusses algorithms for drawing circles and ellipses in computer graphics. It covers: 1. Circle drawing algorithms including using Cartesian coordinates, polar coordinates, and the midpoint circle algorithm which iteratively calculates the midpoint between pixels to determine if they are inside, outside, or on the circle. 2. The midpoint ellipse algorithm which is similar but uses a modified decision parameter calculation that handles two regions for the first quadrant. 3. Key aspects of the algorithms include using octants and circle symmetry to reduce calculations, and translating the drawn shape to be centered at a given point.

1. COMPUTER GRAPHICS
Circles and Ellipses
Lecture 05

2. Scan Converting a Circle

3. Circle Algorithms
• We can generate all points in the circle by calculating only
the points within the sector from x=0 to x=y
• Absolute slope of the curve (tangent to the curve) in this
octant has a magnitude less than or equal to 1.0

4. • Use Pythagoras theorem (for a circle centered at
origin)
• Every point P, lying on the circle can be found by
equation given in the diagram
4
x
r
y
y
x x
y
r
 2 2
,P x r x 
Strategy 1: Cartesian form
x2 + y2 = r2

5. Cartesian Form
• A circle centered at (xc,yc):
• For a better circle use octants and circle symmetry,
stepping from xc-r to where x=y
2
c
2
c
cc
22
c
2
c
x)-(x-r±y=y
r+xtor-xfromsteps
r=)y-(y+)x-(x

6. Strategy 2: Polar Form
• Polar coordinates
• A circle centered at (xc,yc):
• All these methods have long execution time
sin(angle)r+y=y
cos(angle)r+x=x
c
c

7. Circle Algorithms
The Circle Function:
If any point (x,y) is inside the circle, fcirc(x,y)<0
If any point (x,y) is on the circle, fcirc(x,y)=0
If any point (x,y) is outside the circle, fcirc(x,y)>0
222
),( ryxyxfcirc 

8. Midpoint Circle Algorithm
• Principle of the midpoint algorithm
• Find the values from one octant of a circle centered at (0,0),
then find the remaining octants by symmetry, then translate
to (xc, yc).
• The circle function is the decision parameter.
• Calculate the circle function for the midpoint between two
pixels.

9. Midpoint Circle Algorithm
(from Donald Hearn and Pauline Baker)

10. Midpoint Circle Algorithm
•If pk<0, midpoint is inside the circle and yk is closer
• we select yk
•If pk>=0, midpoint is outside or on the circle and yk-1
is closer
• we select yk-1

11. Midpoint Circle Algorithm
1. Input radius r and circle center (xc, yc), then set the
coordinates for the first point on the circumference of a
circle centered on the origin as (xo, y0) = (0, r).
2. Calculate the initial value of the decision parameter as
p0 = 5/4 – r
3. At each xk, from k=0, perform the following test:
if pk<0, next point to plot along the circle centered on (0,0) is
(xk+1, yk) and pk+1 = pk + 2 xk+1 + 1
otherwise, next point to plot is (xk+ 1, yk - 1)
and pk+1 = pk + 2 xk+1 + 1 - 2 yk+1
where 2 xk+1 = 2 xk + 2, and 2 yk+1 = 2 yk - 2

12. Midpoint Circle Algorithm
4. Determine symmetry points in the other seven
octants.
5. Move each calculated pixel position (x, y) onto the
circular path centered at (xc, yc) and plot the
coordinate values:
x = x + xc, y = y + yc
6. Repeat steps 3 through 5 until x >= y.

13. Midpoint Circle Algorithm

14. Drawing Ellipse
• Ellipses can be drawn similarly using a modified
midpoint algorithm.
• Similar algorithms can be used to display polynomials,
exponential functions, trigonometric functions, conics,
etc.

15. Ellipse

16. Ellipse

17. Ellipse

18. Ellipse Algorithms
222222
),( yxxyellipse rryrxryxf 
If any point (x,y) is inside the ellipse, fellipse(x,y)<0
If any point (x,y) is on the ellipse, fellipse(x,y)=0
If any point (x,y) is outside the ellipse, fellipse(x,y)>0
• Decision parameter Pk (incremental) has different
equations for the two regions for first quadrant of the
ellipse
• Work with region 1 parameters, and switch to region 2
if the slope on the curve becomes greater than 1
• This is equivalent to continuing in region 1until
2r2
yx>=2r2
xy

19. References
• Computer Graphics with OpenGL, Hearn and Baker,
2010, 4th edition