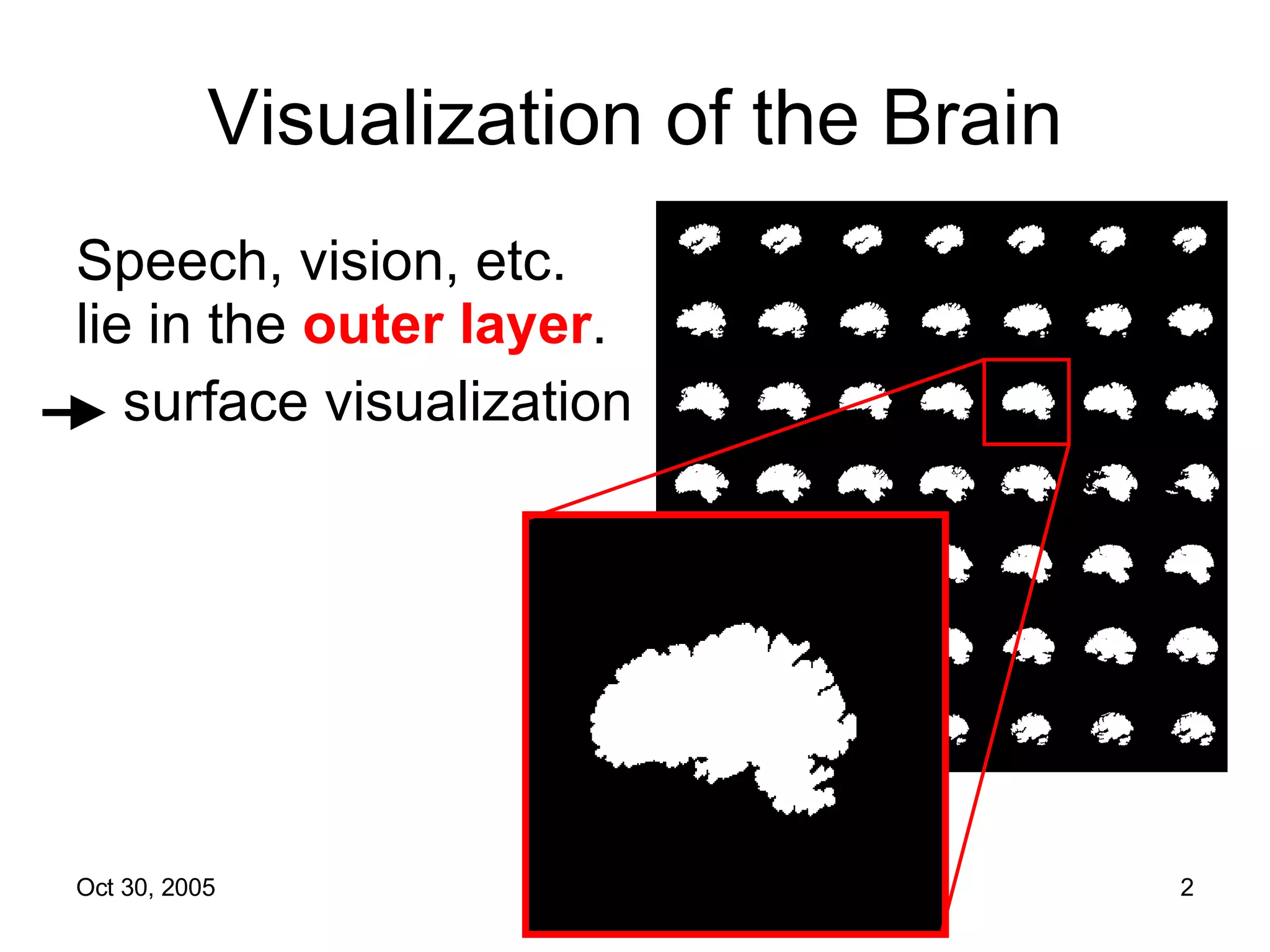
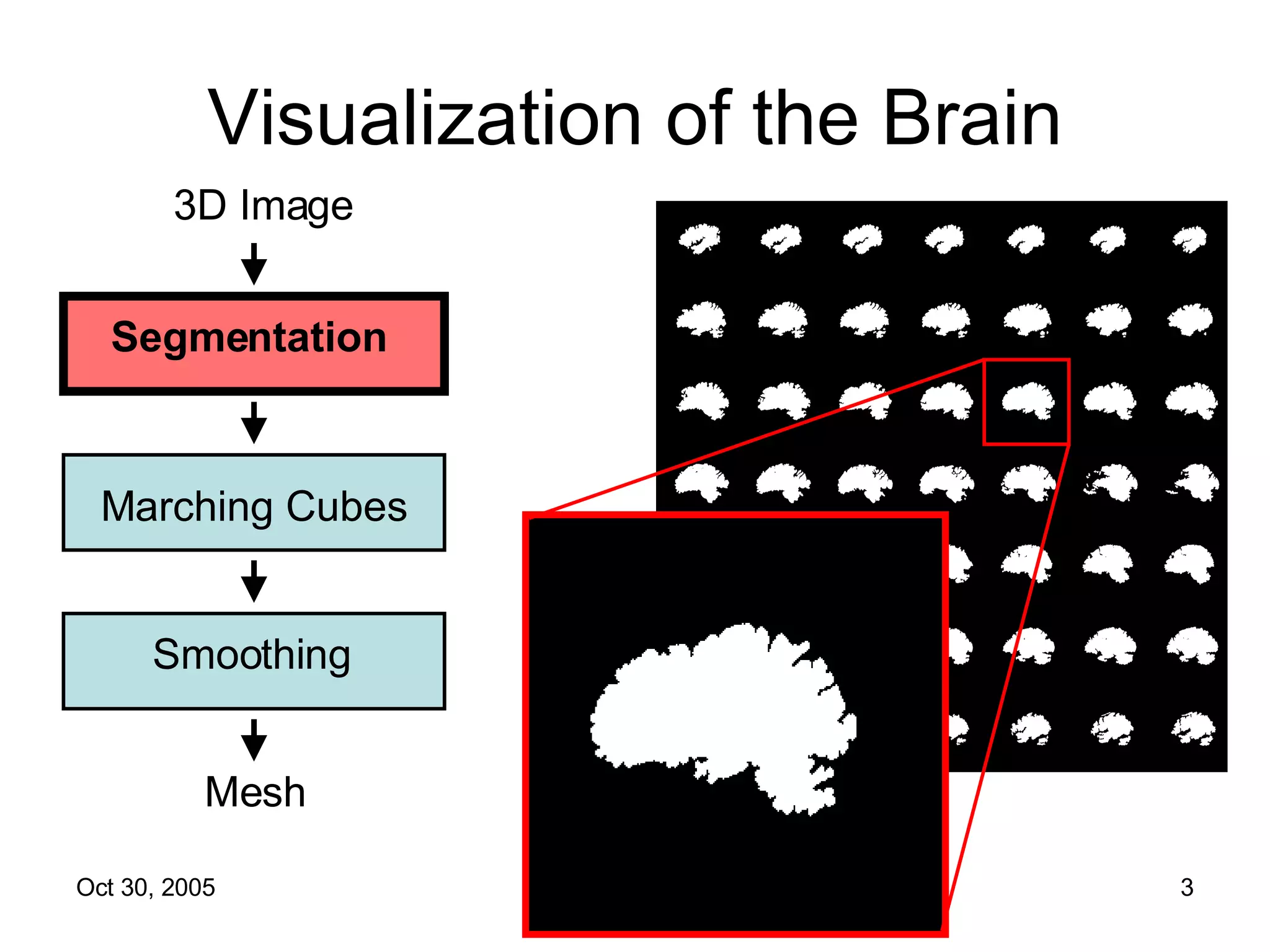
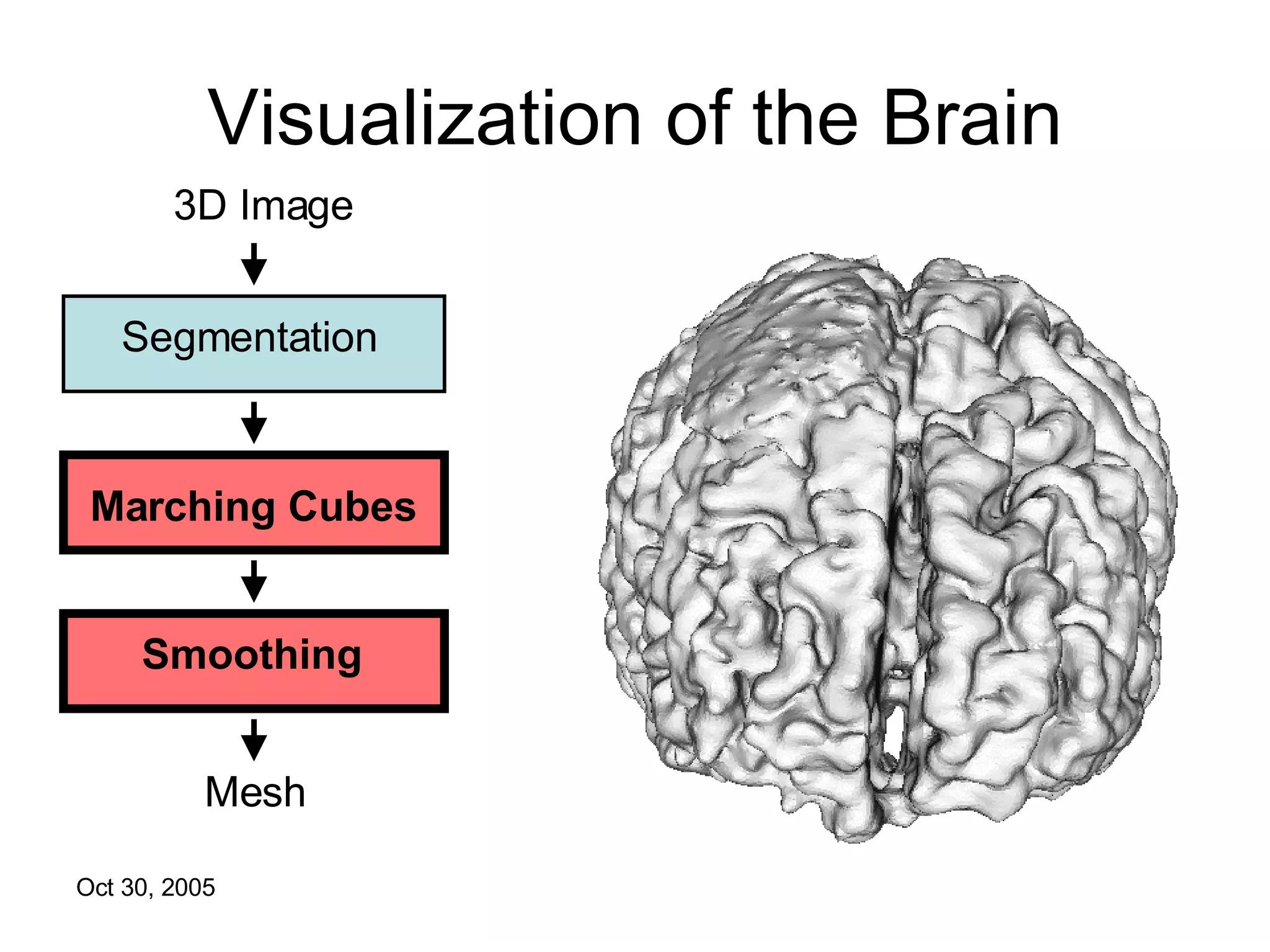
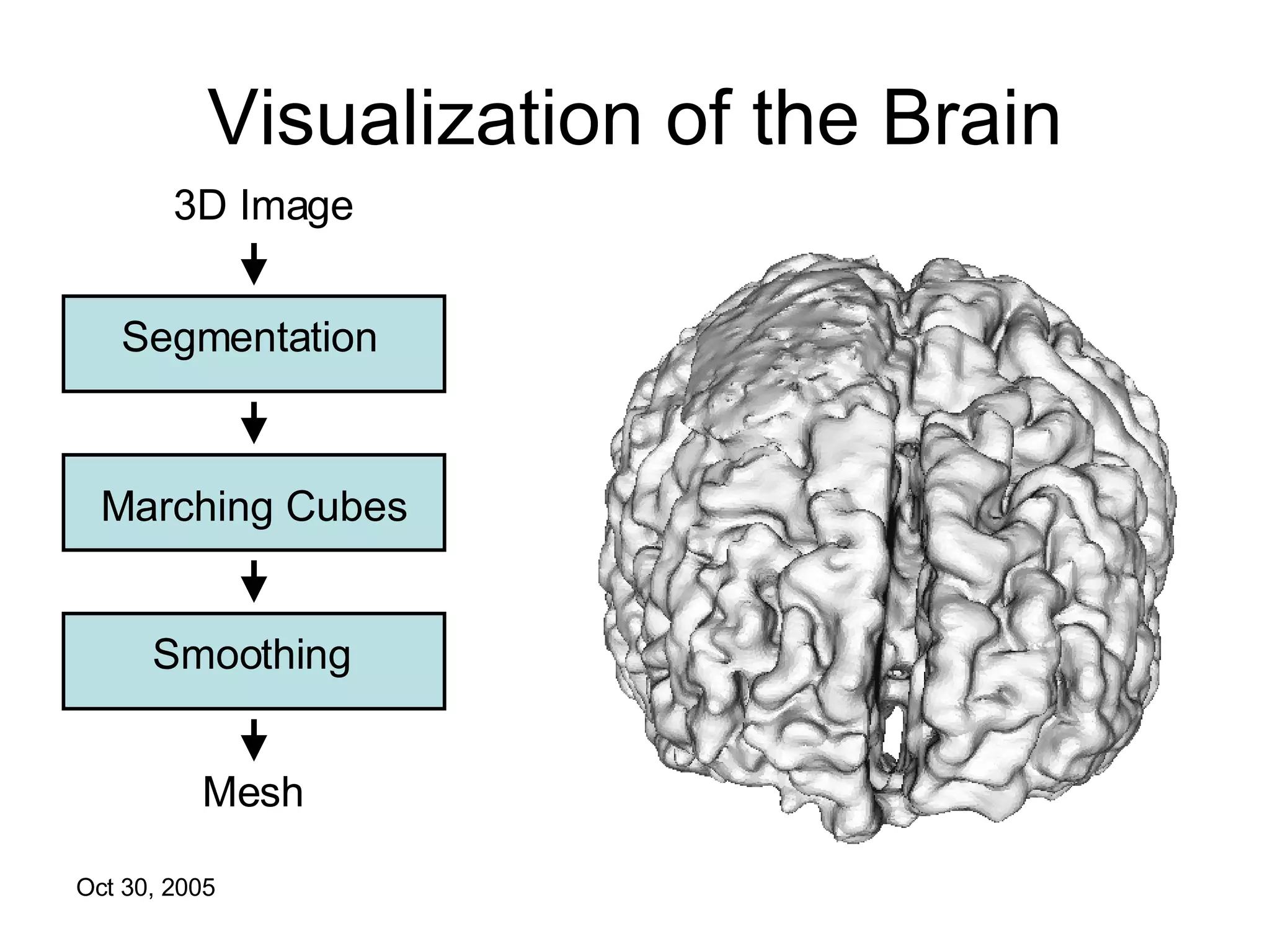
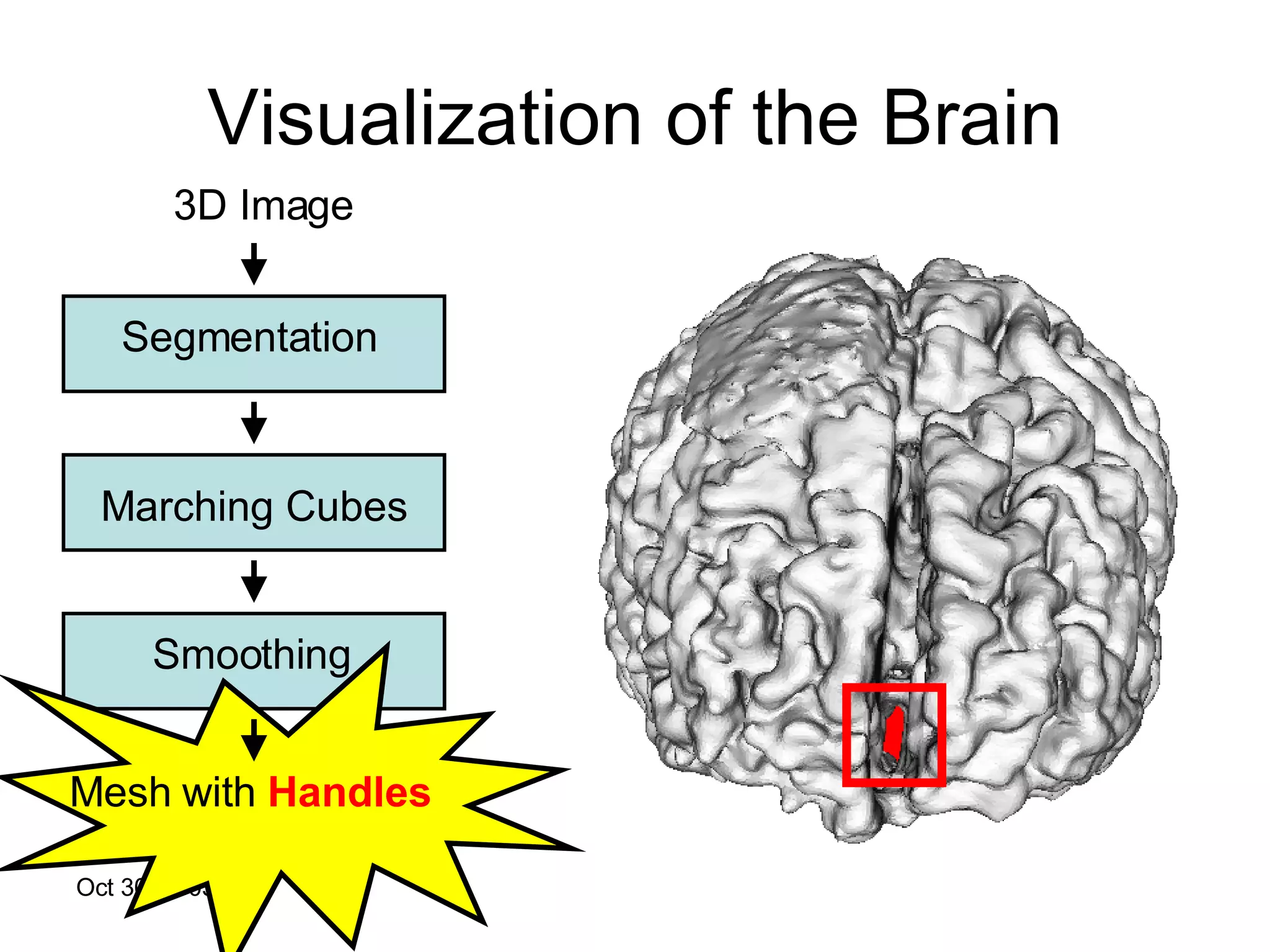
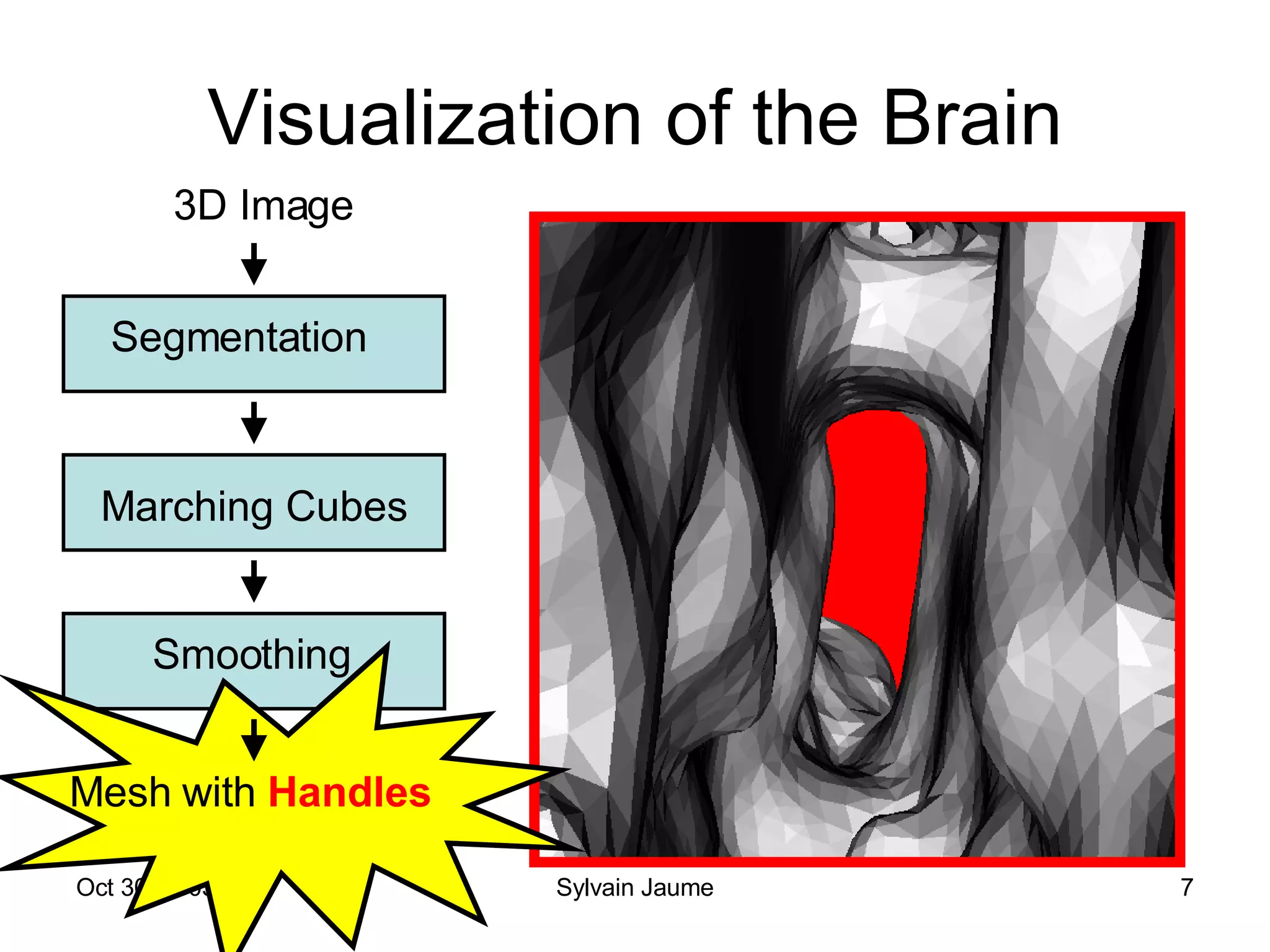
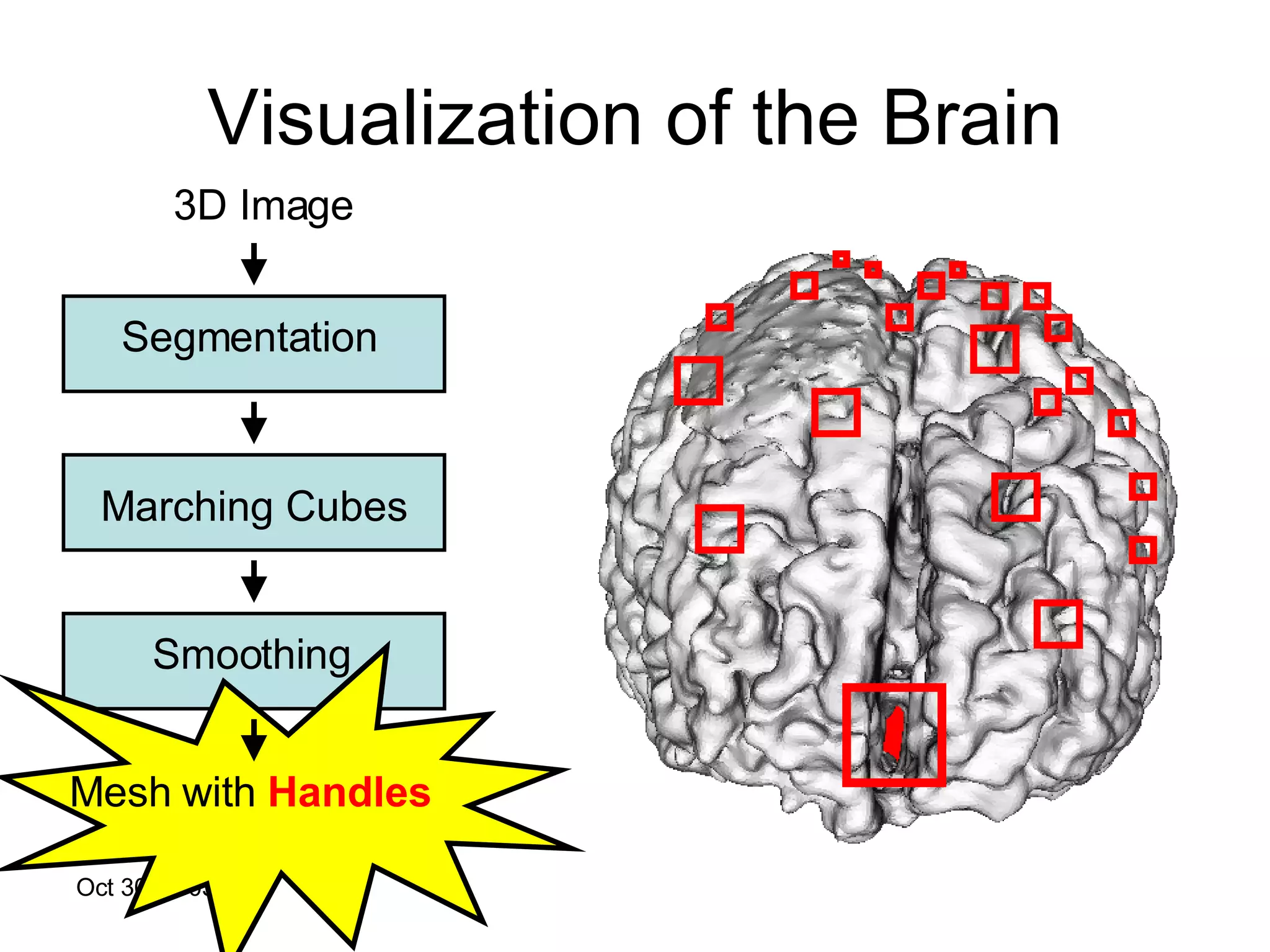
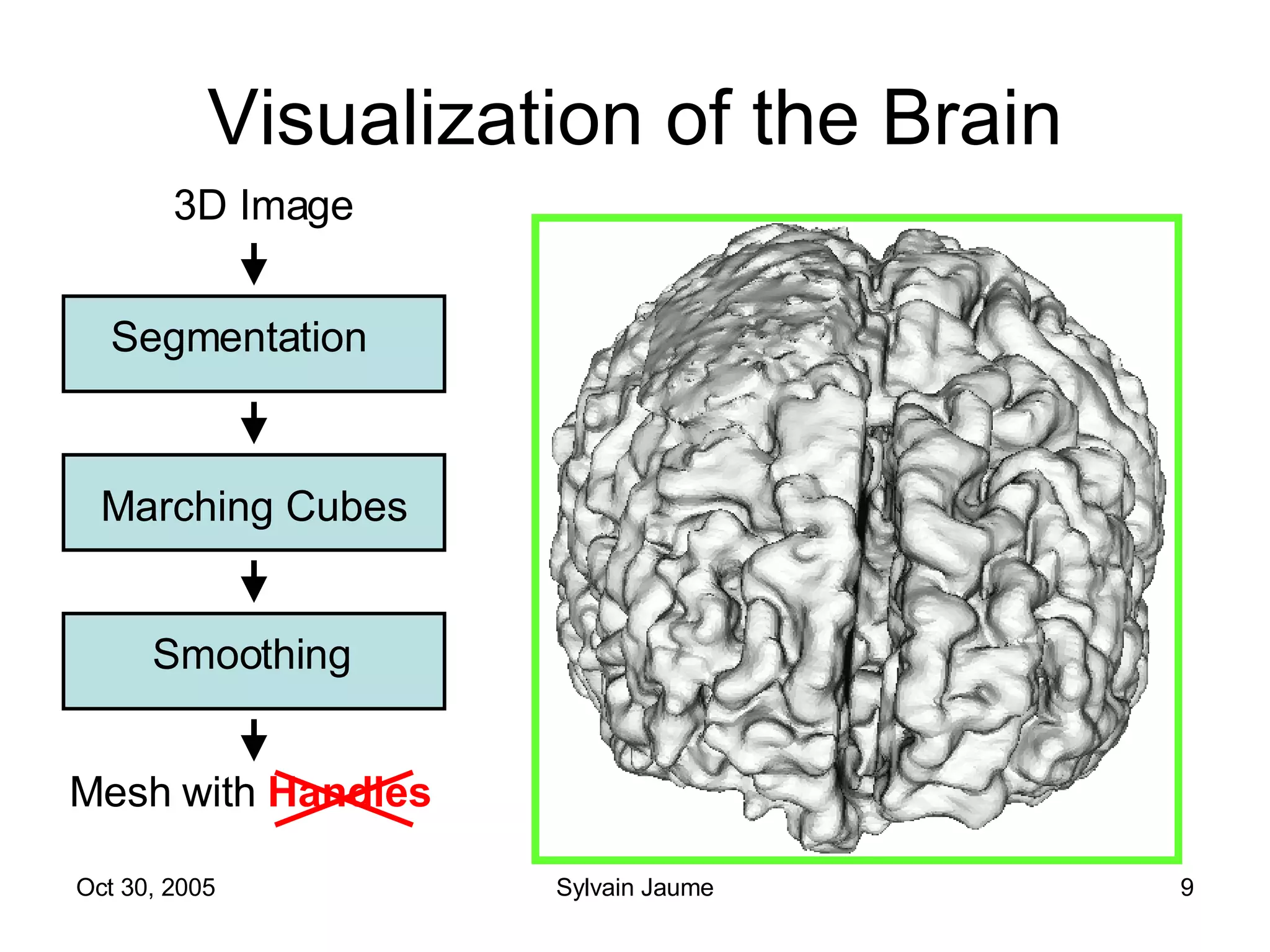
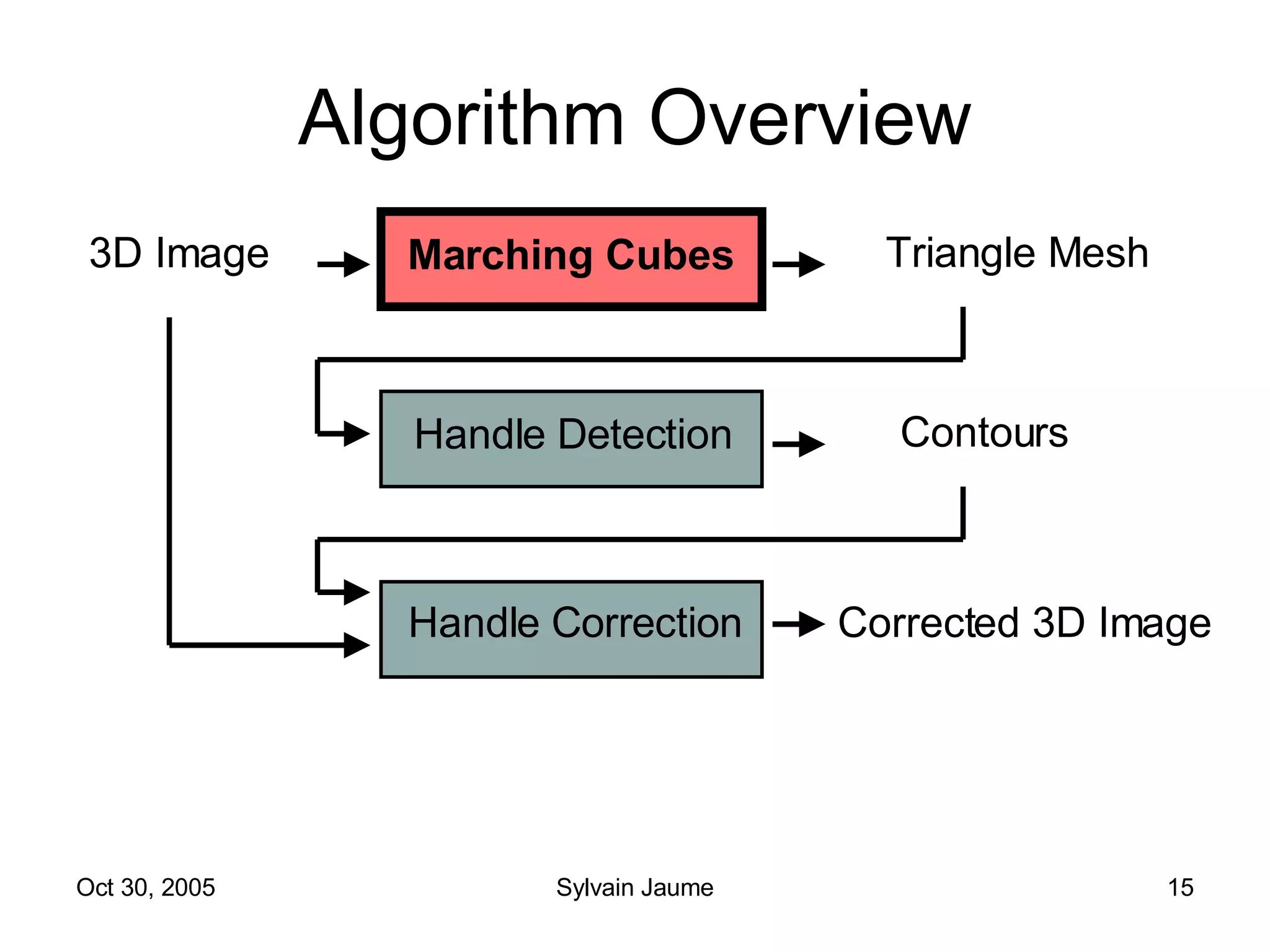
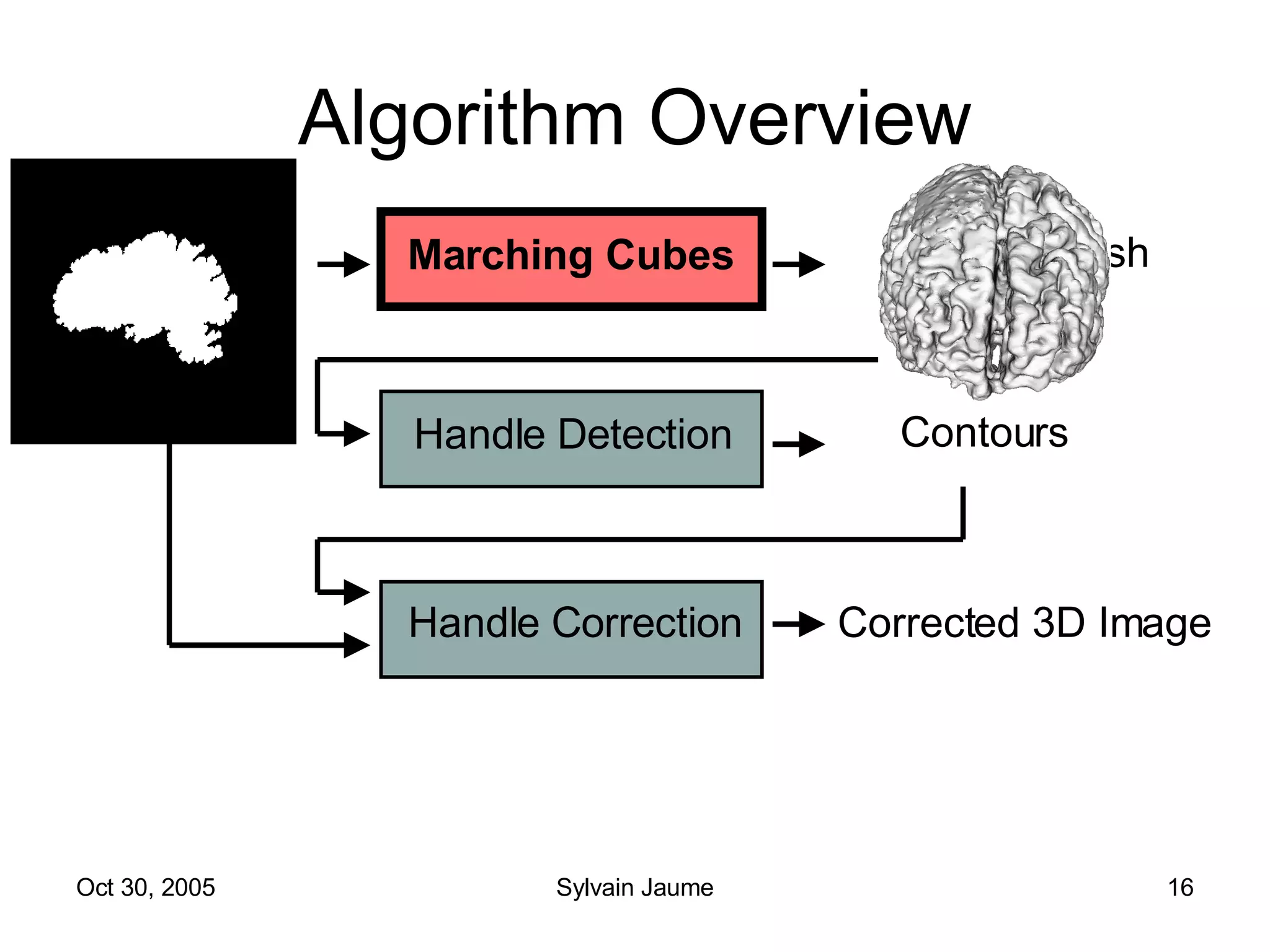
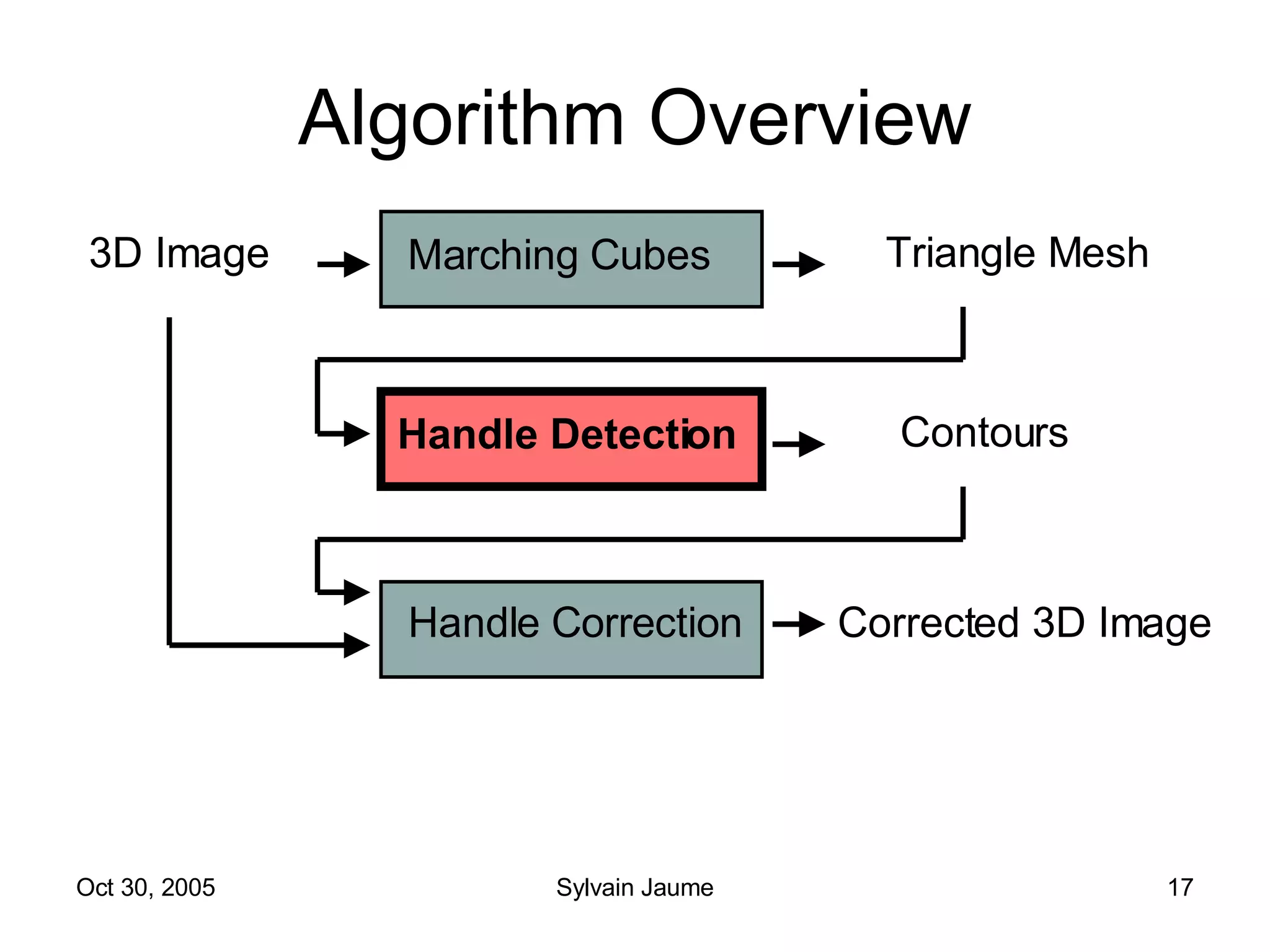
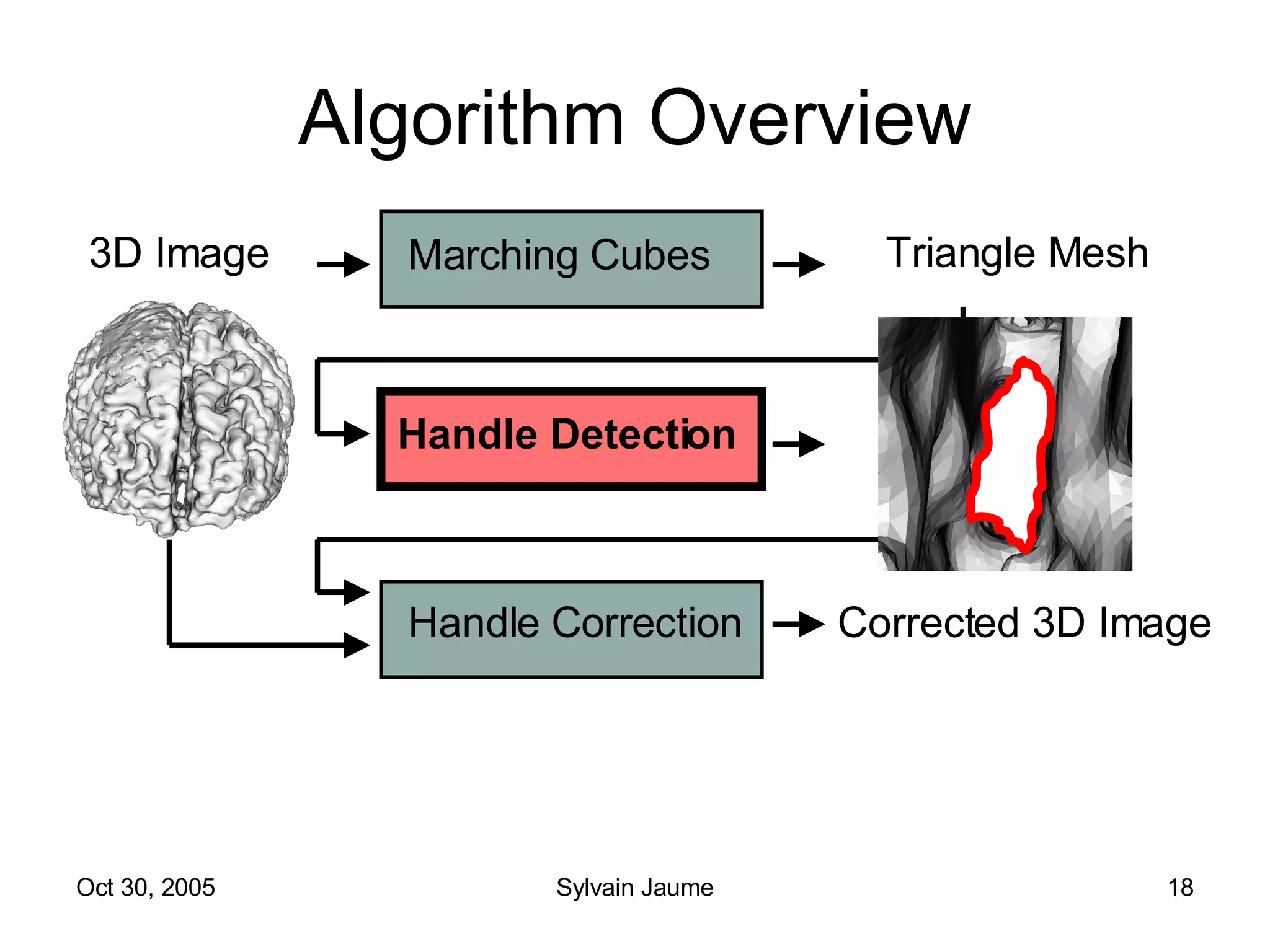
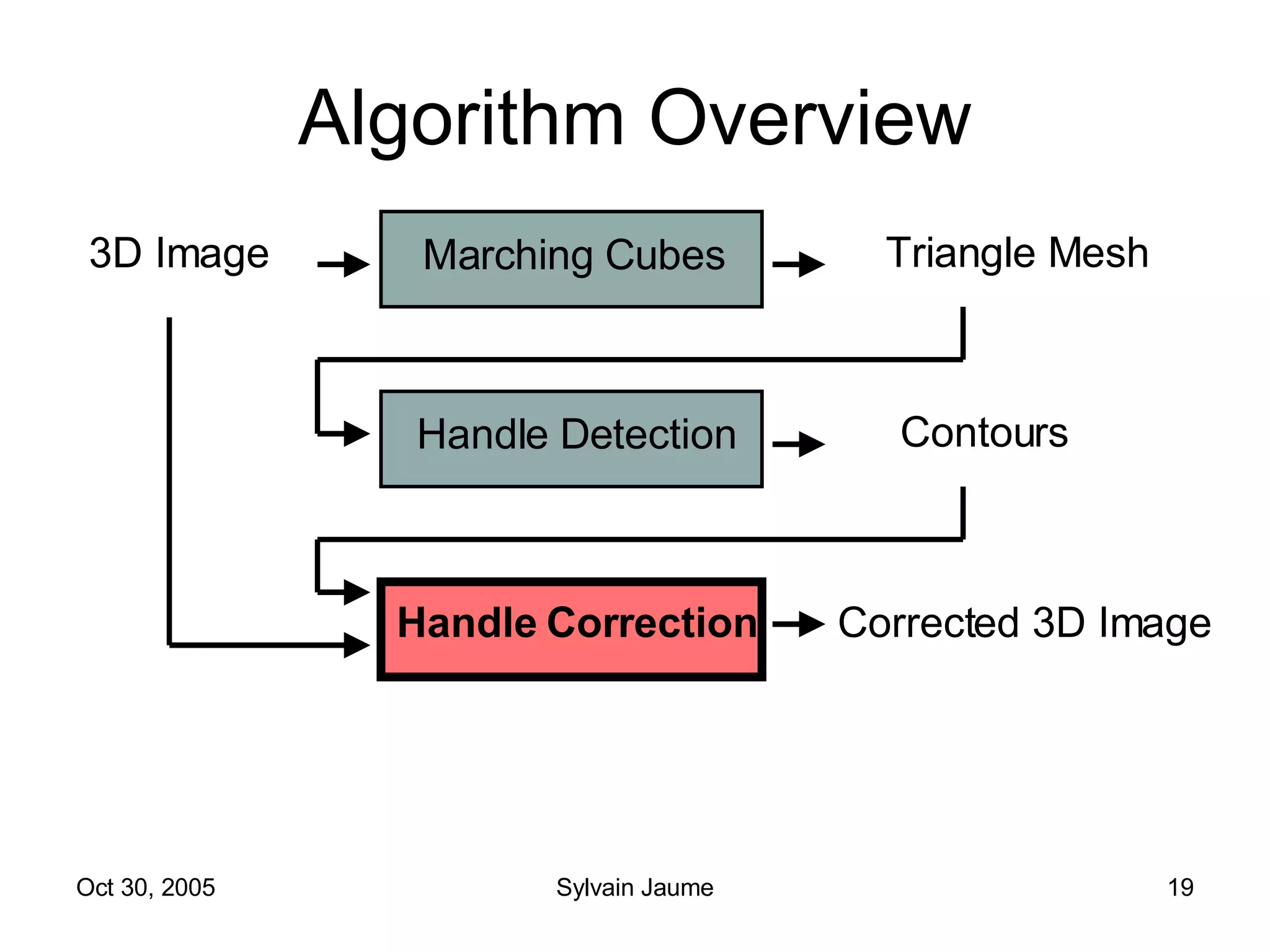
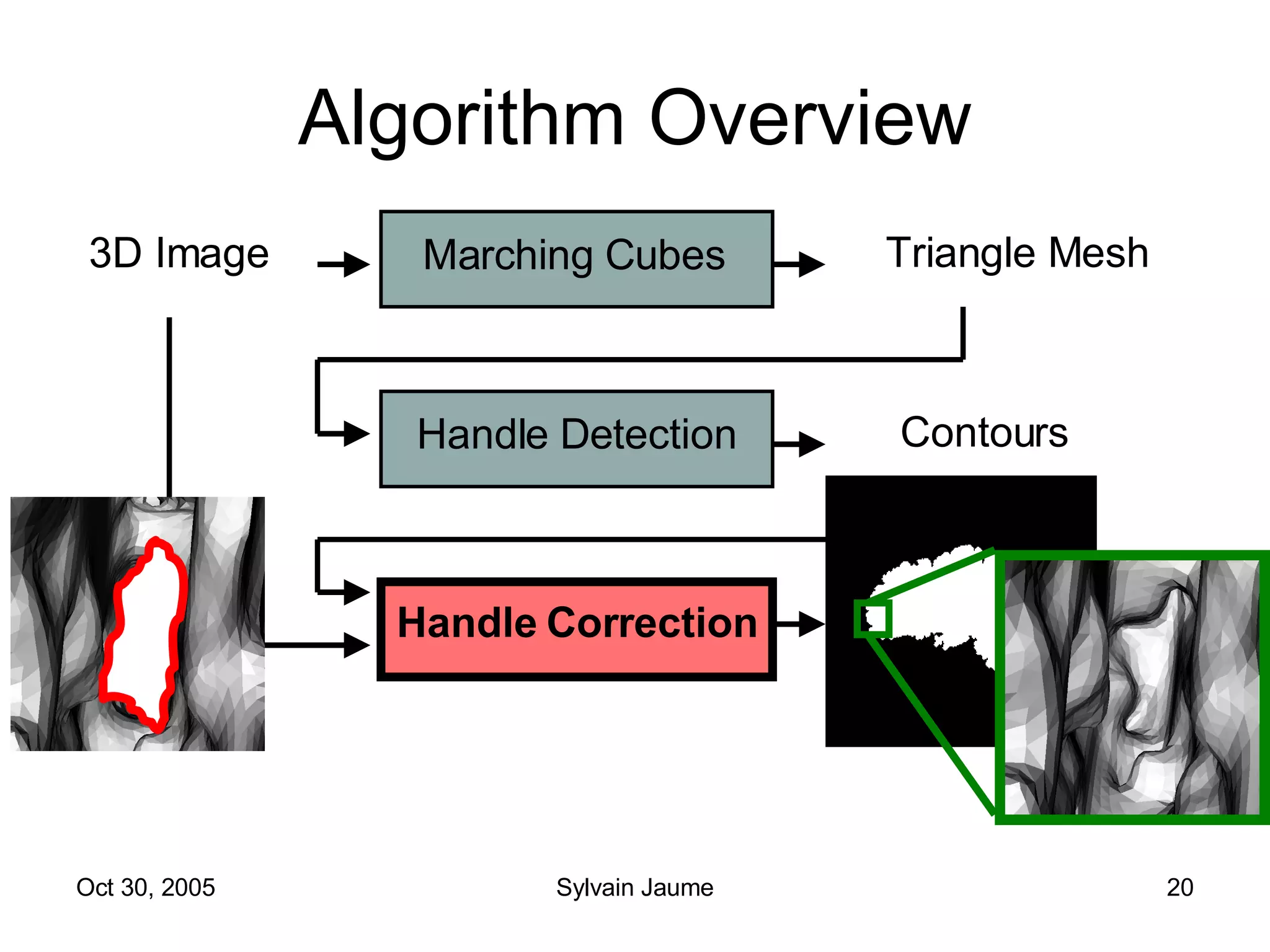
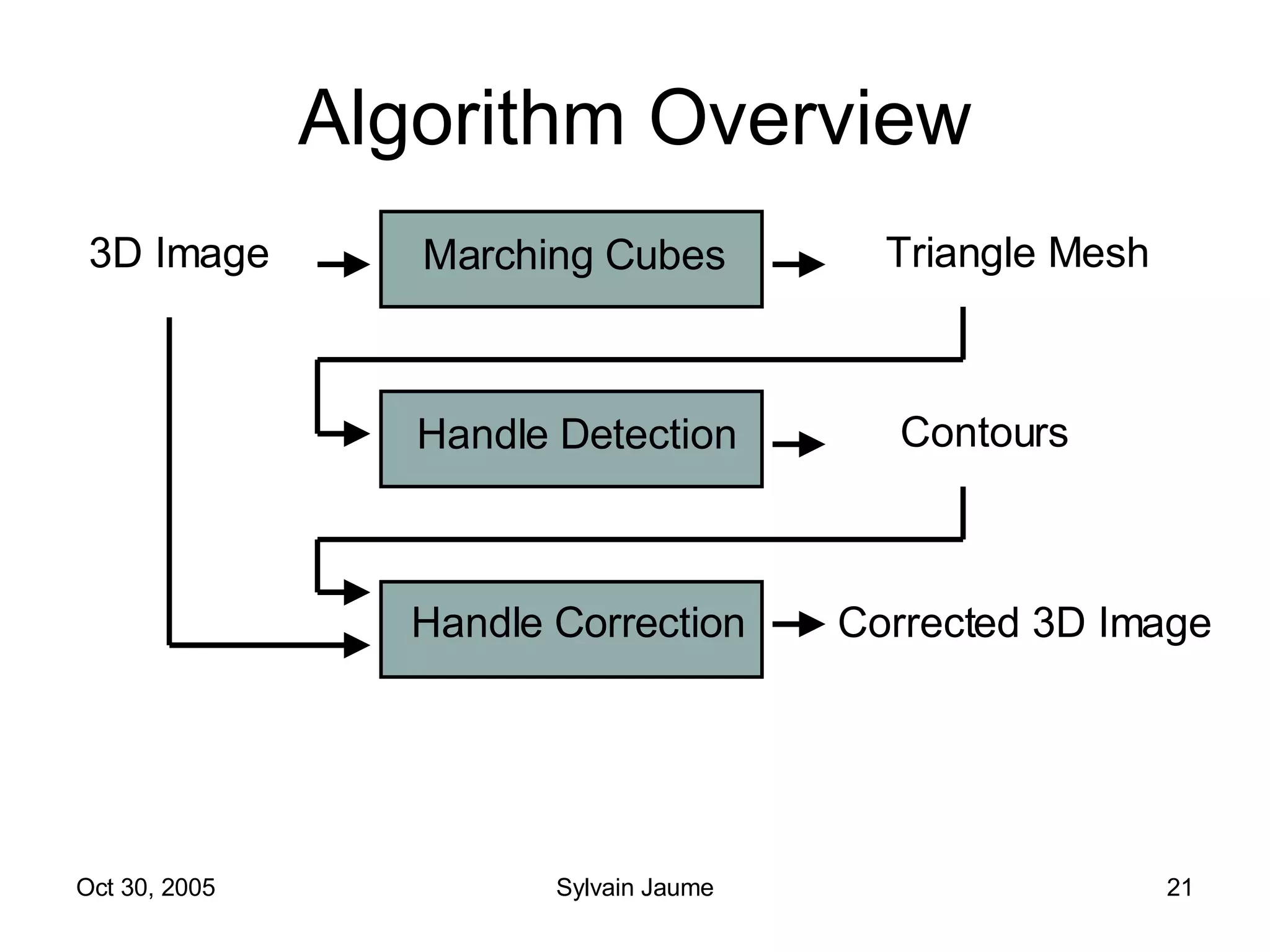
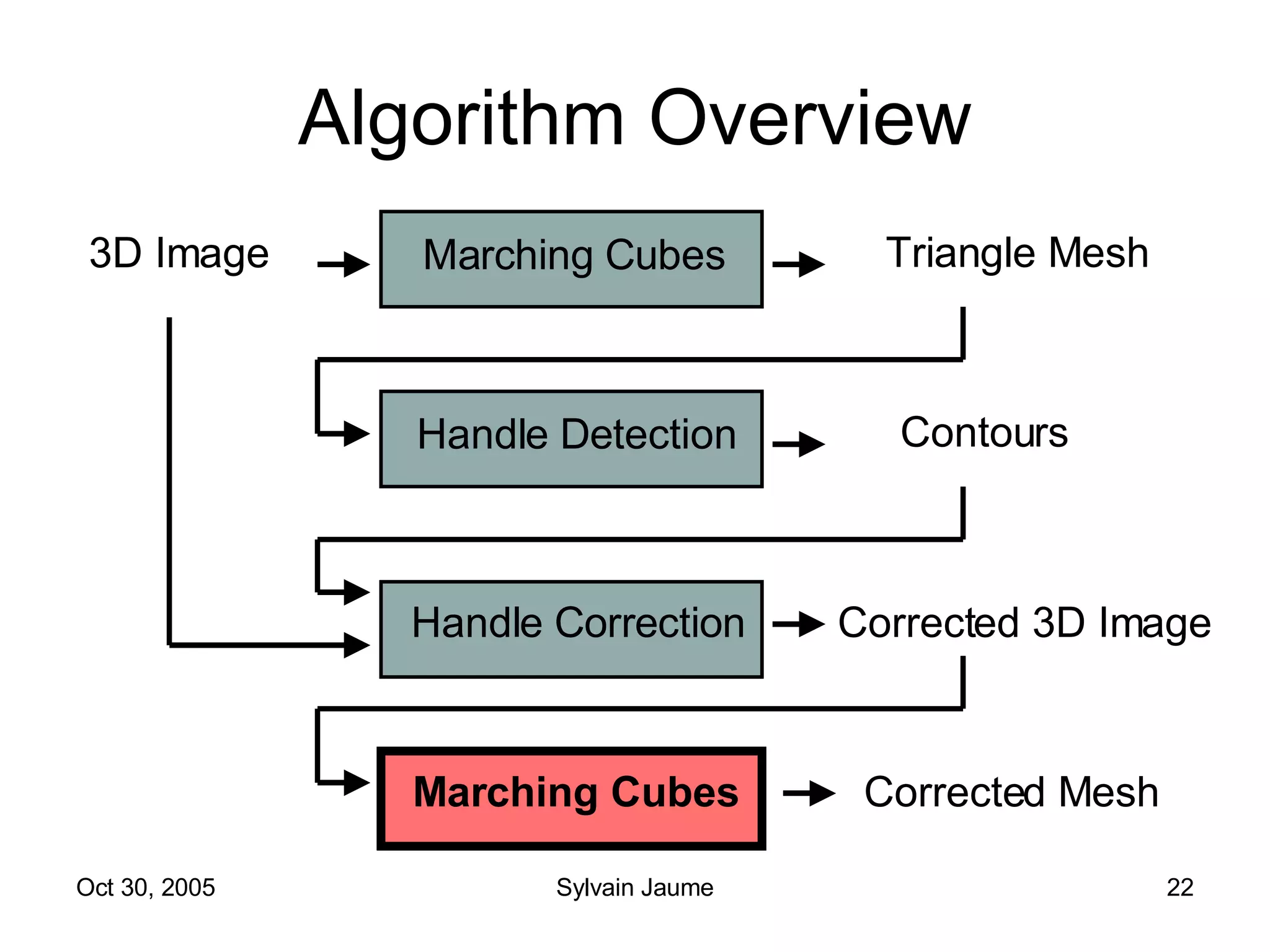
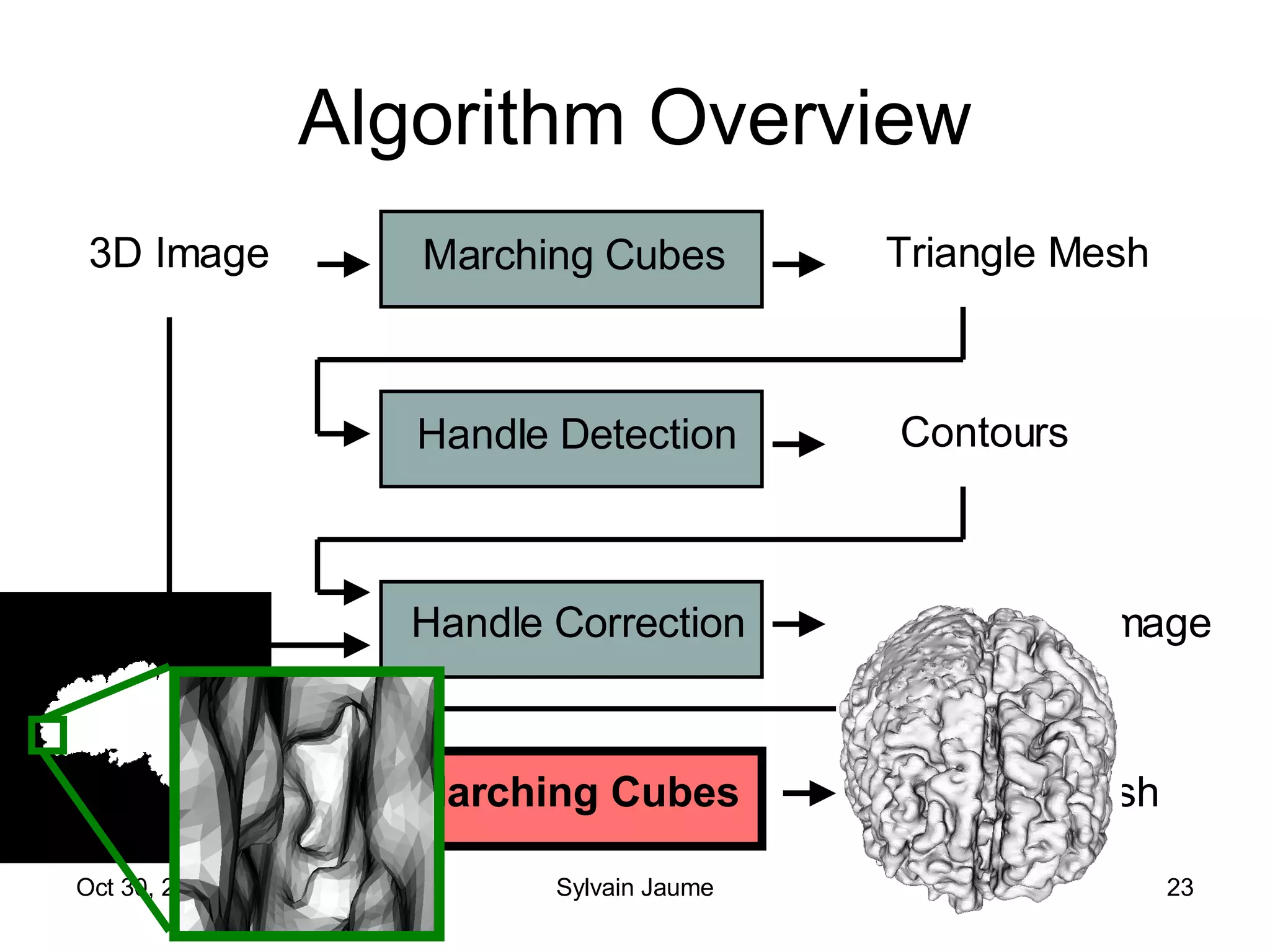
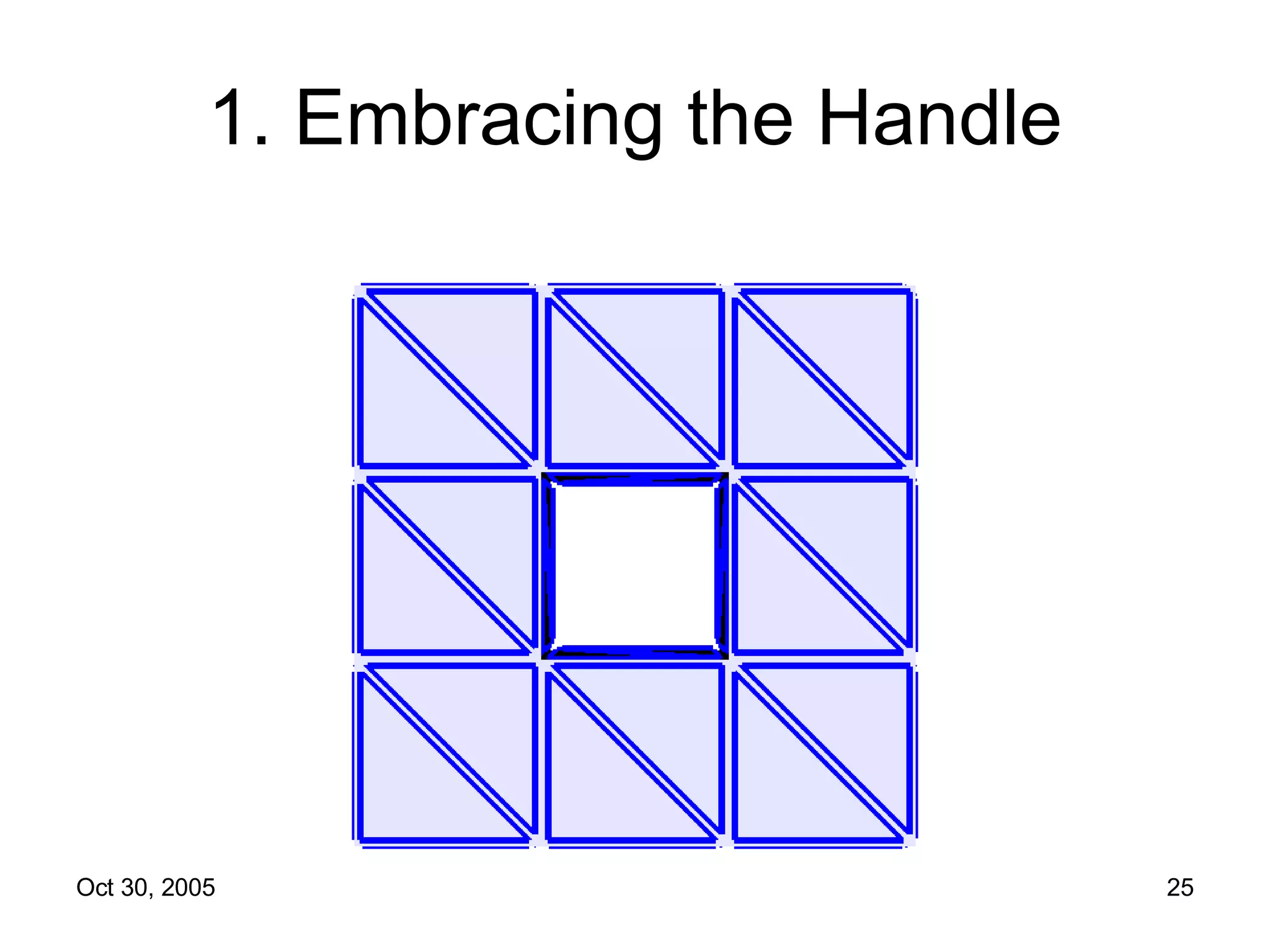
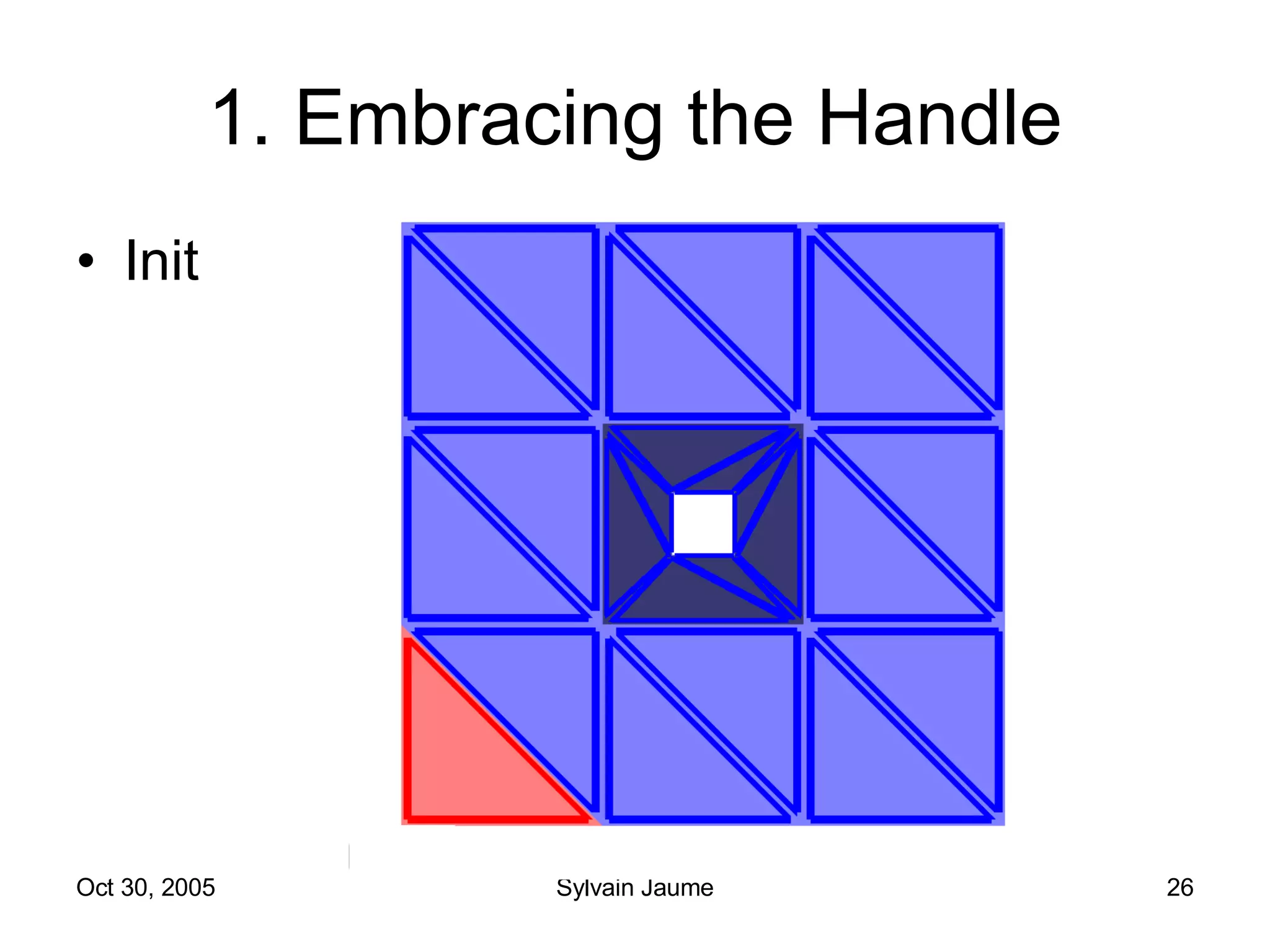
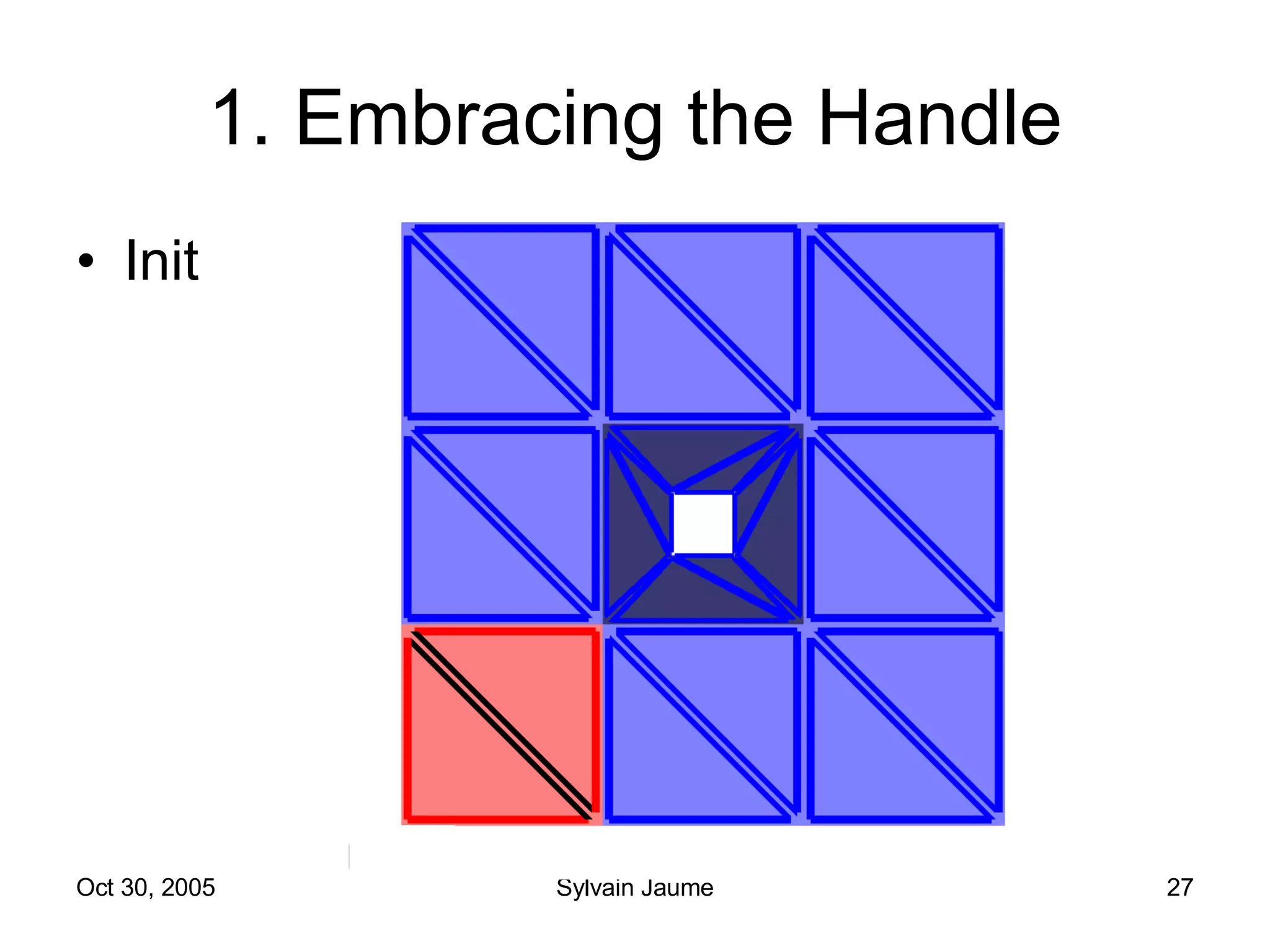
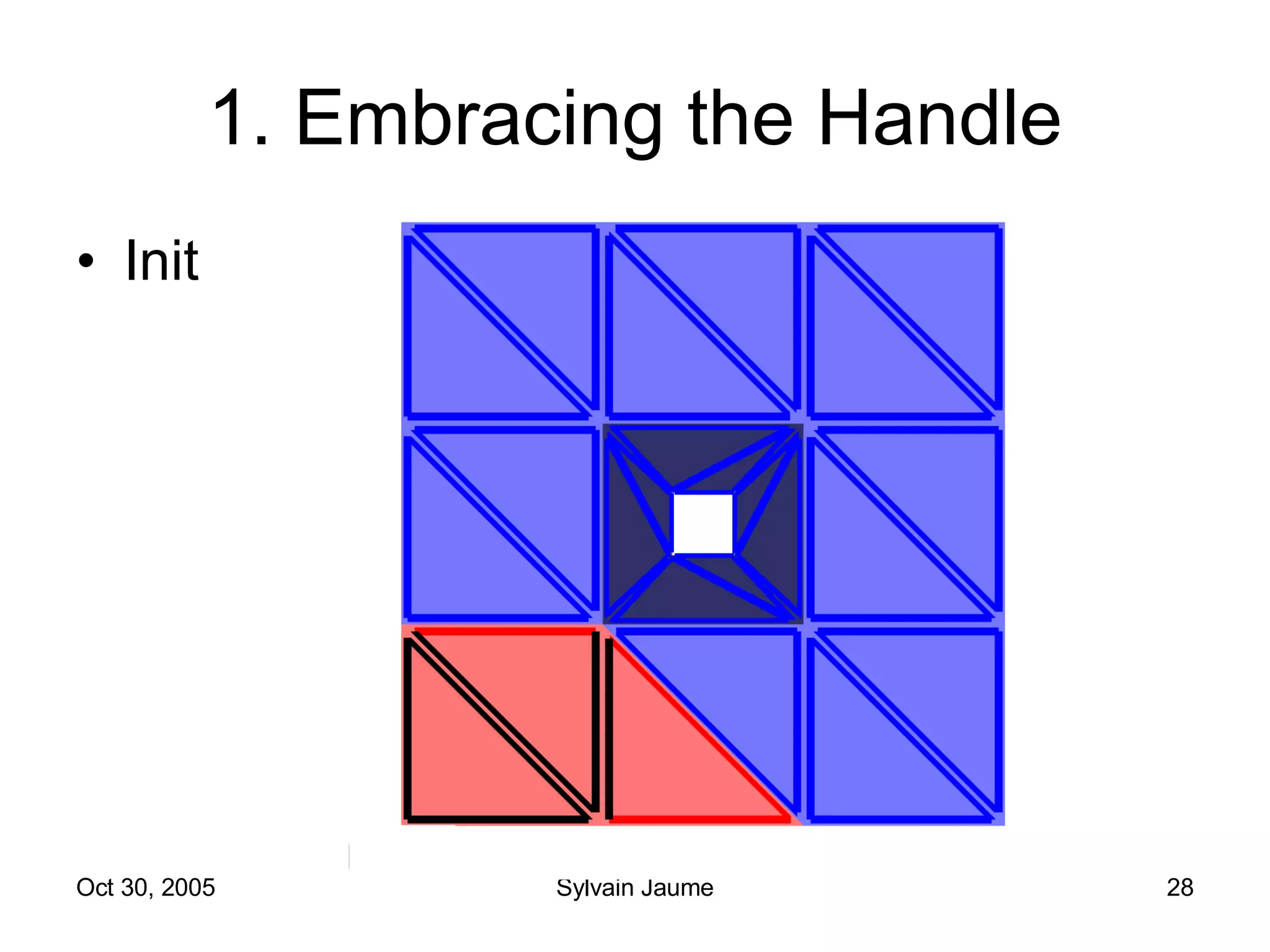
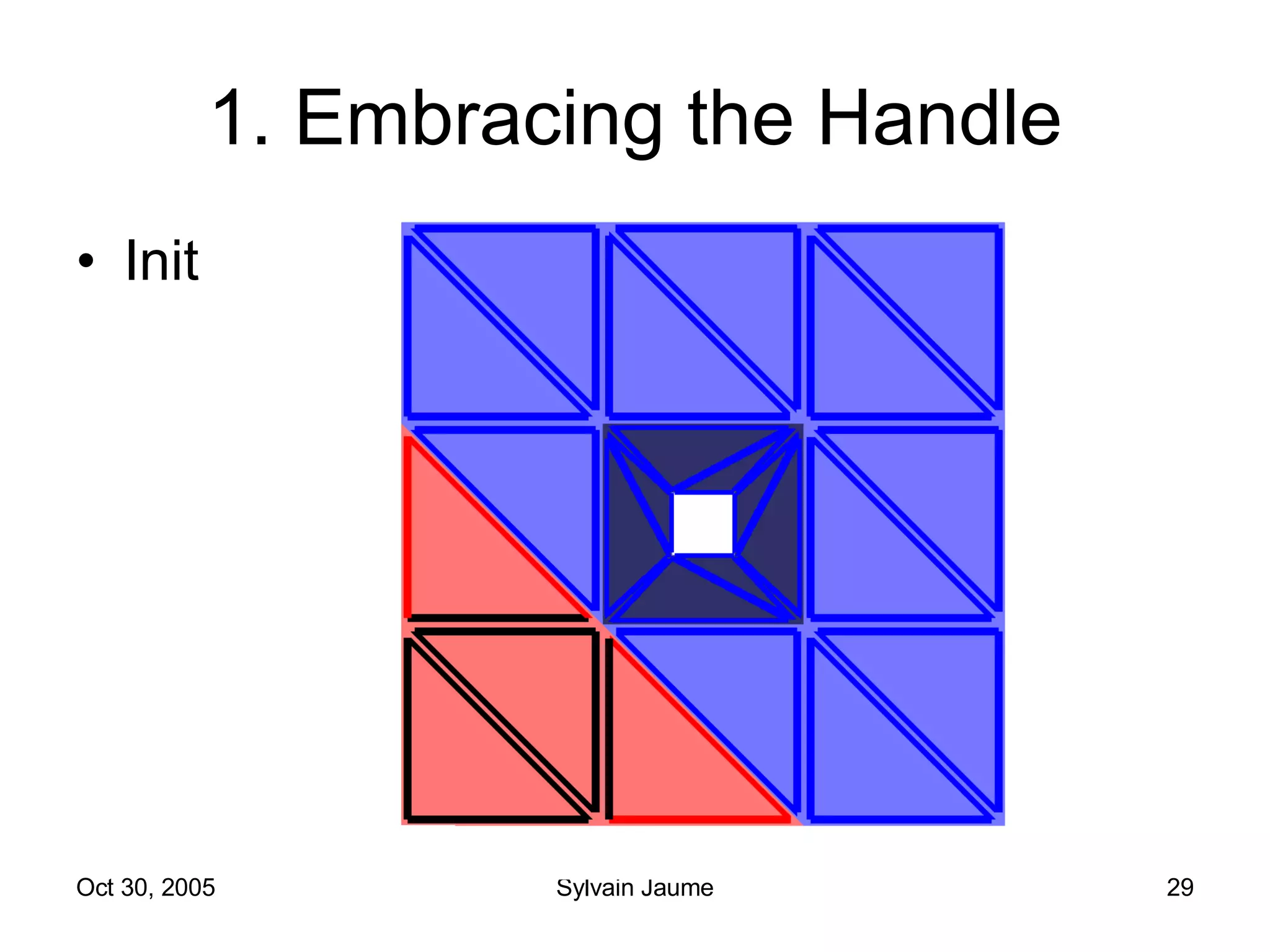
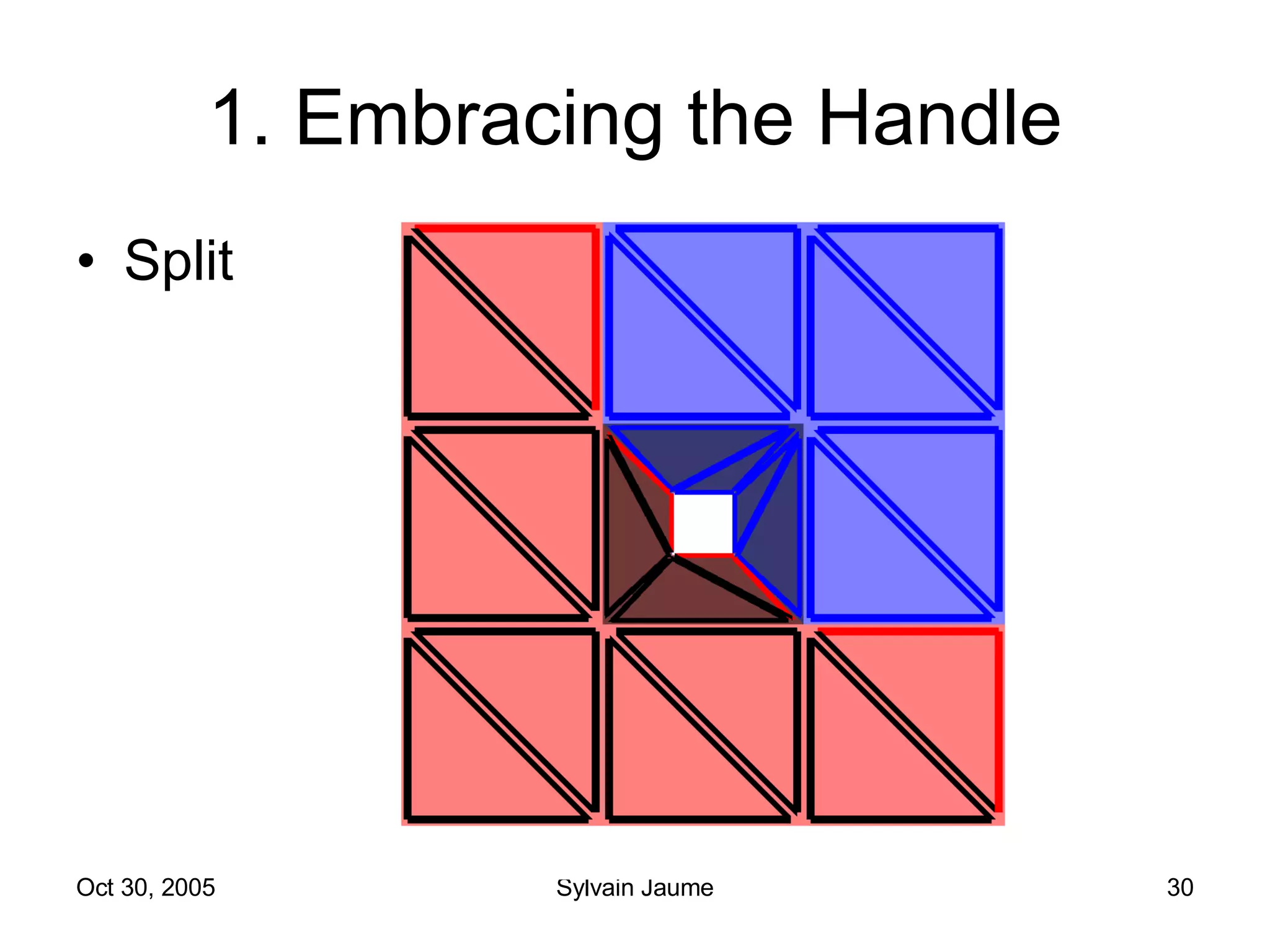
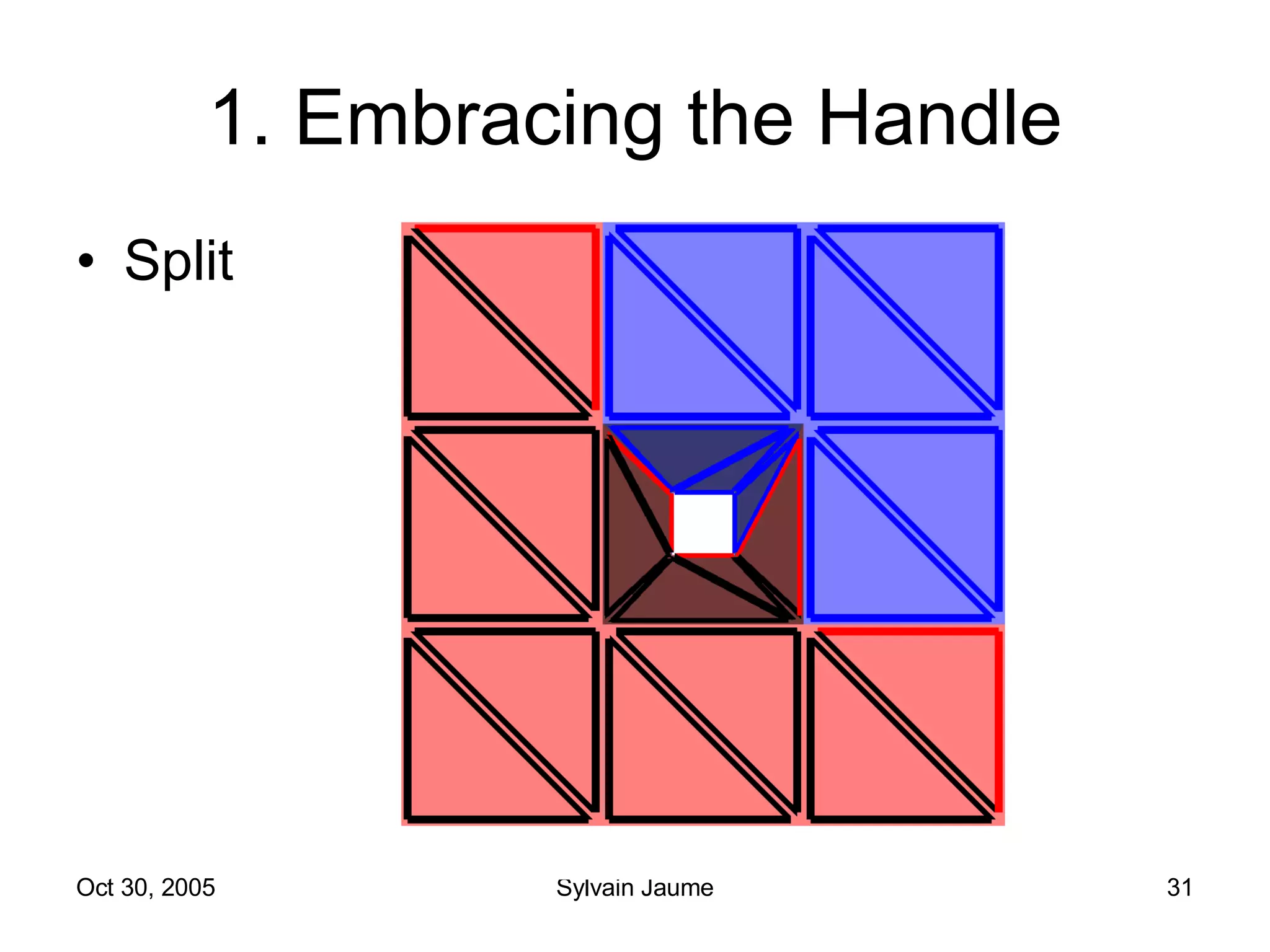
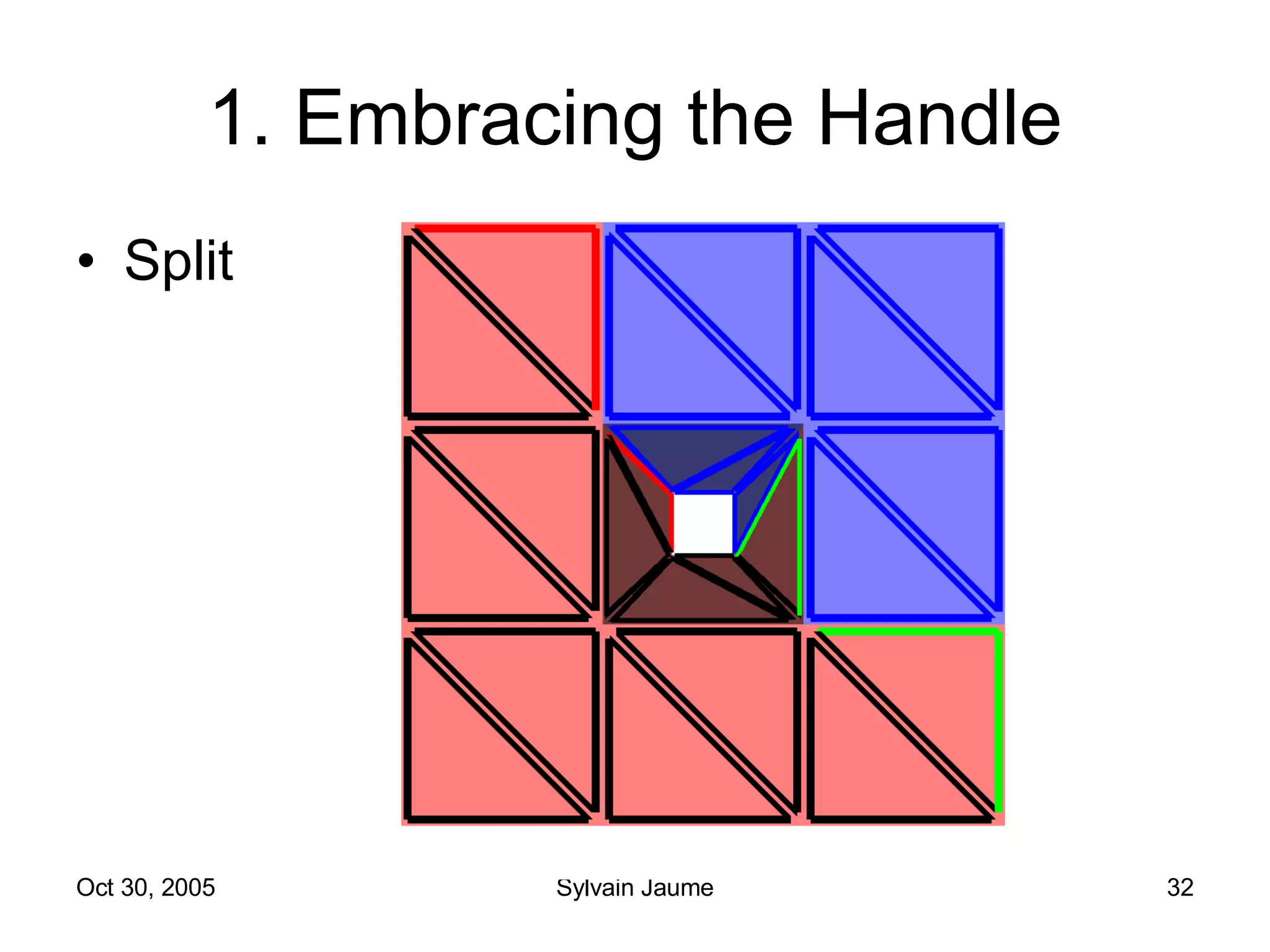
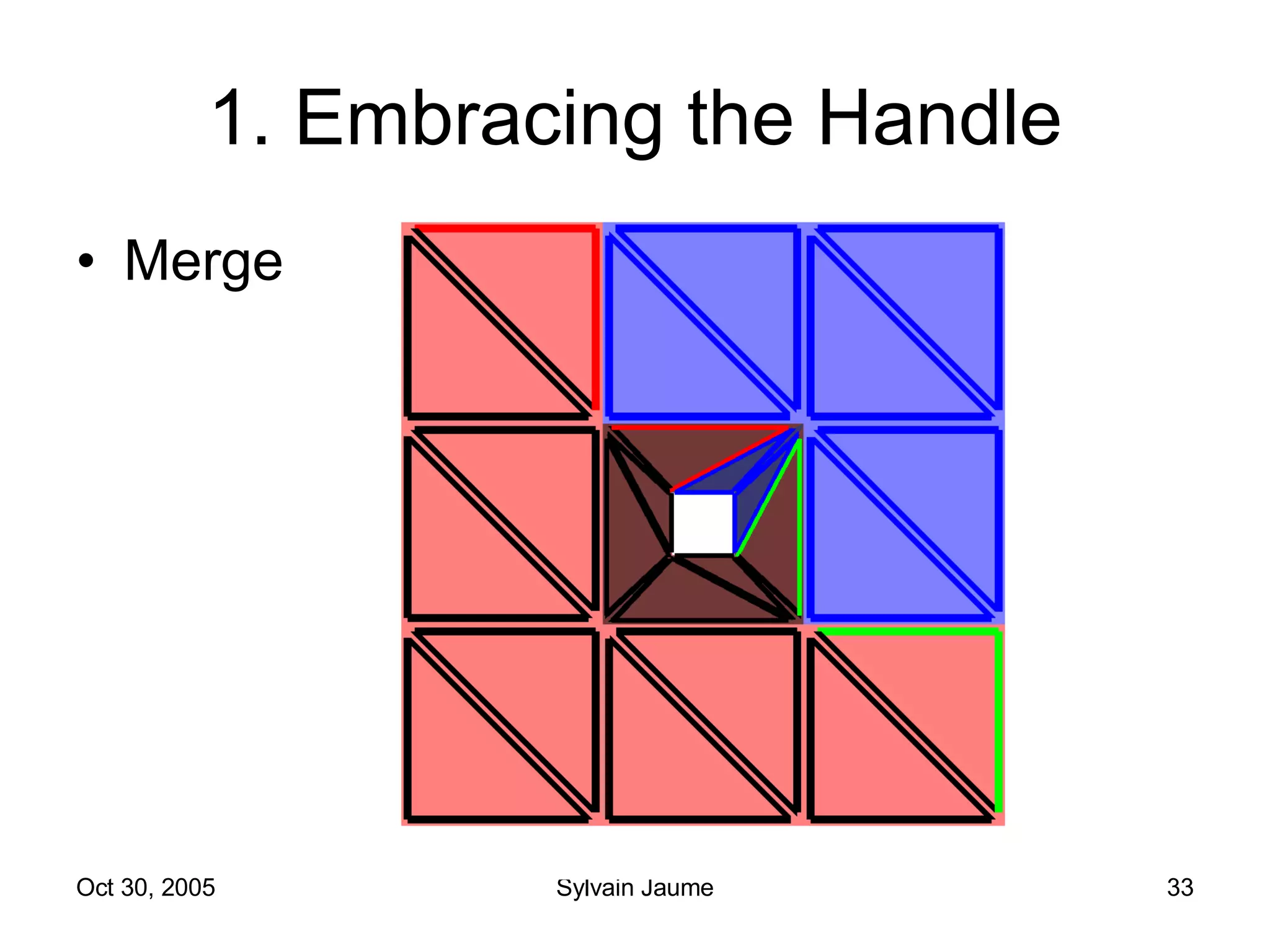
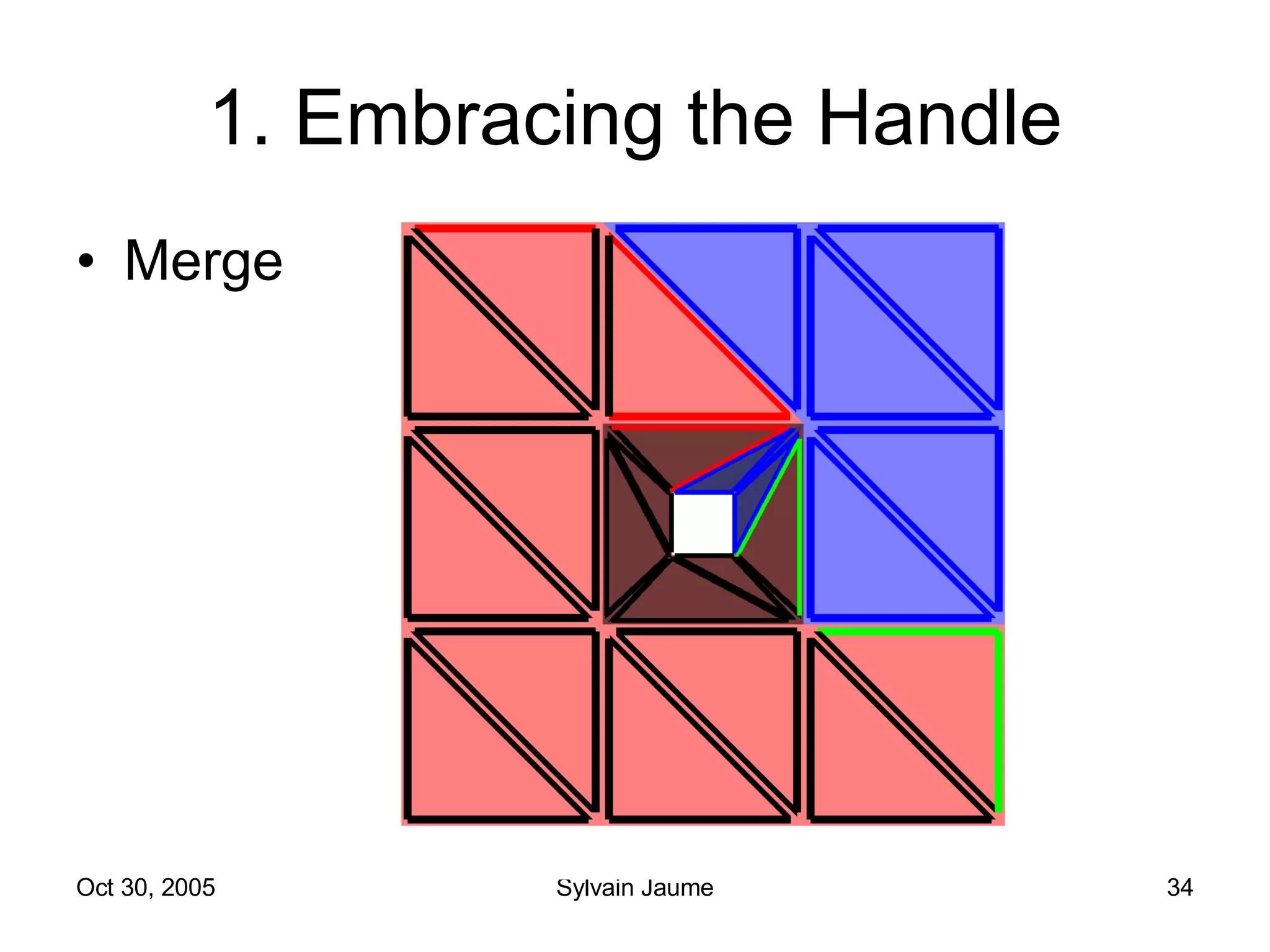
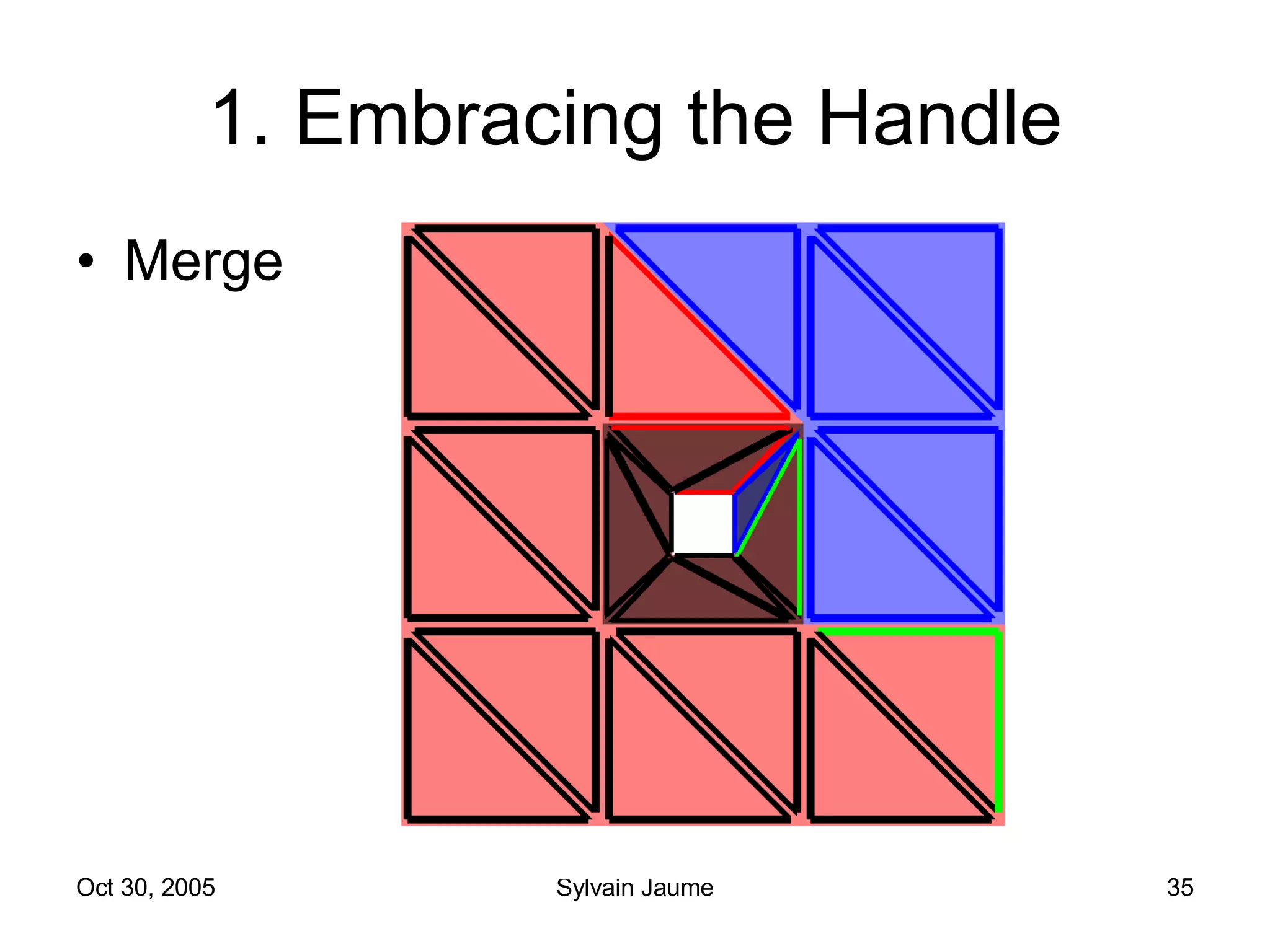
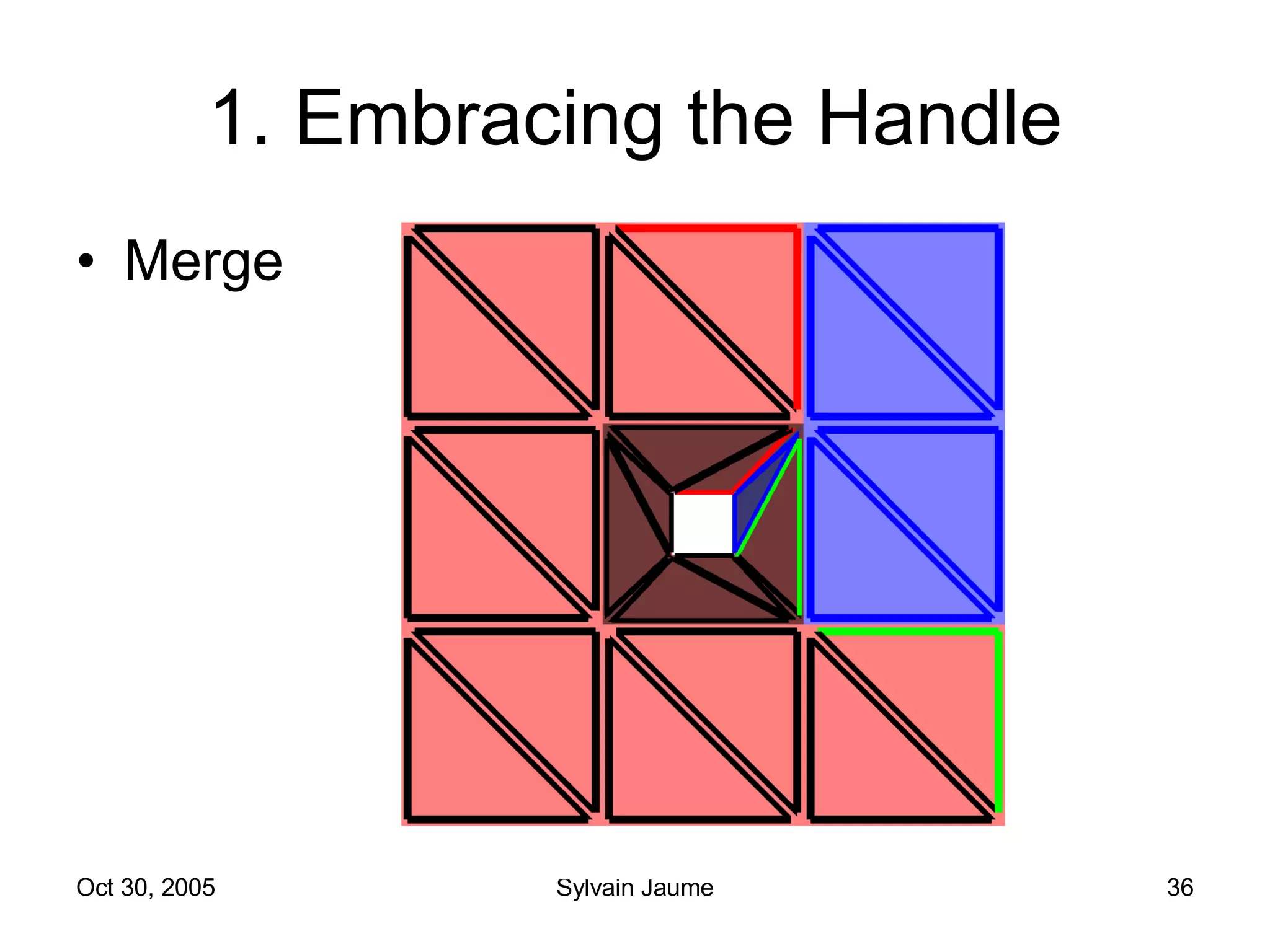
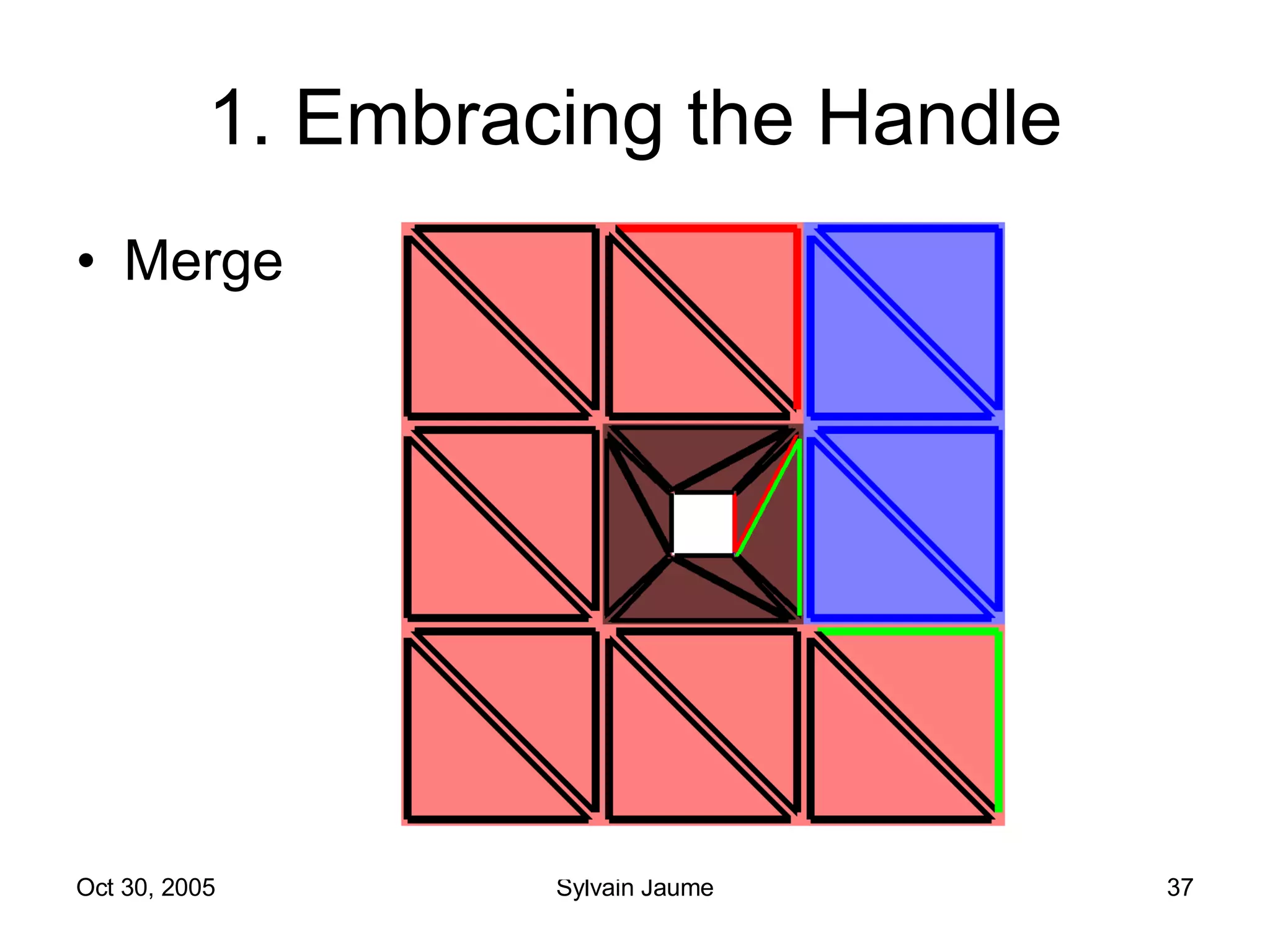
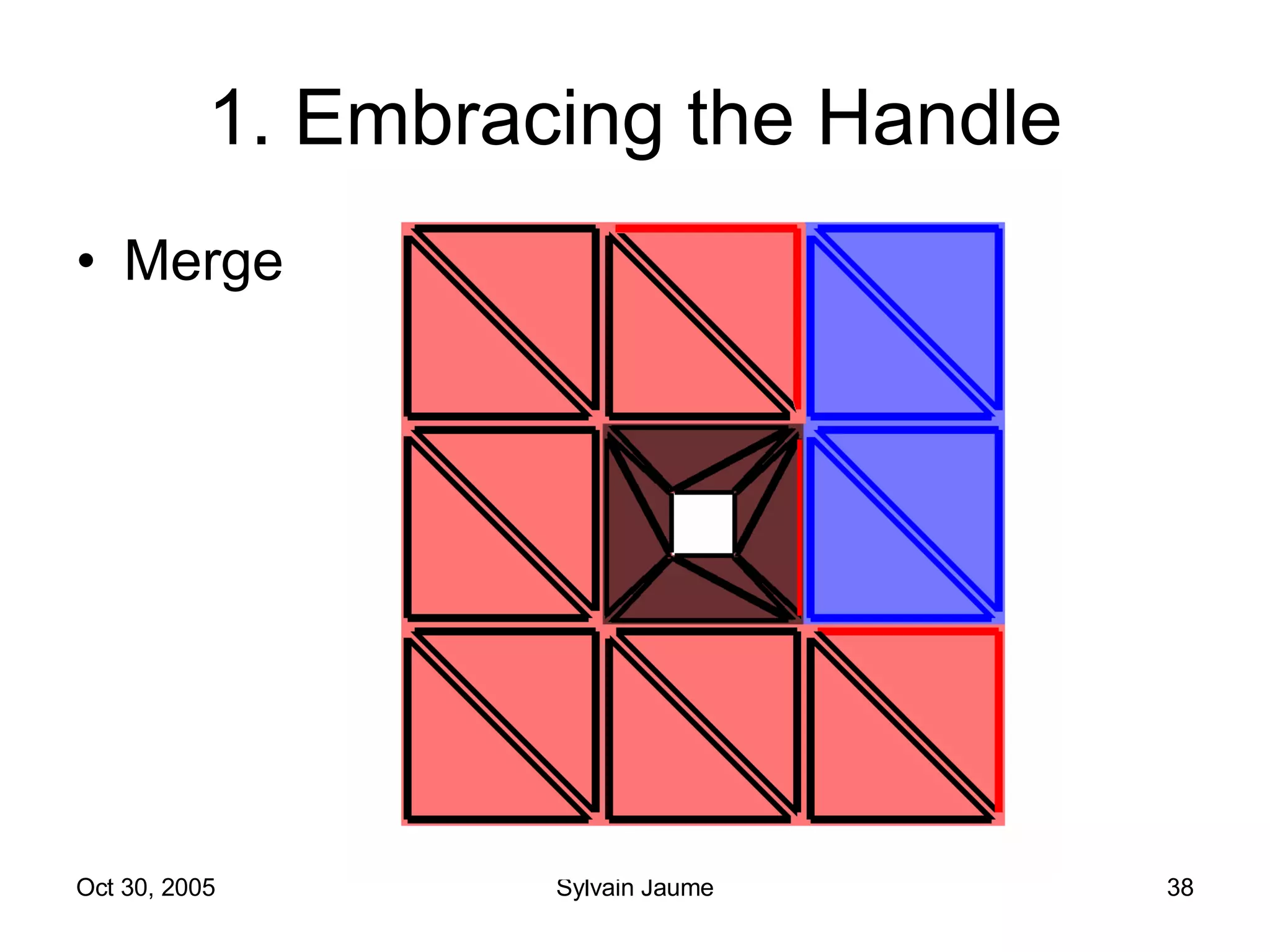
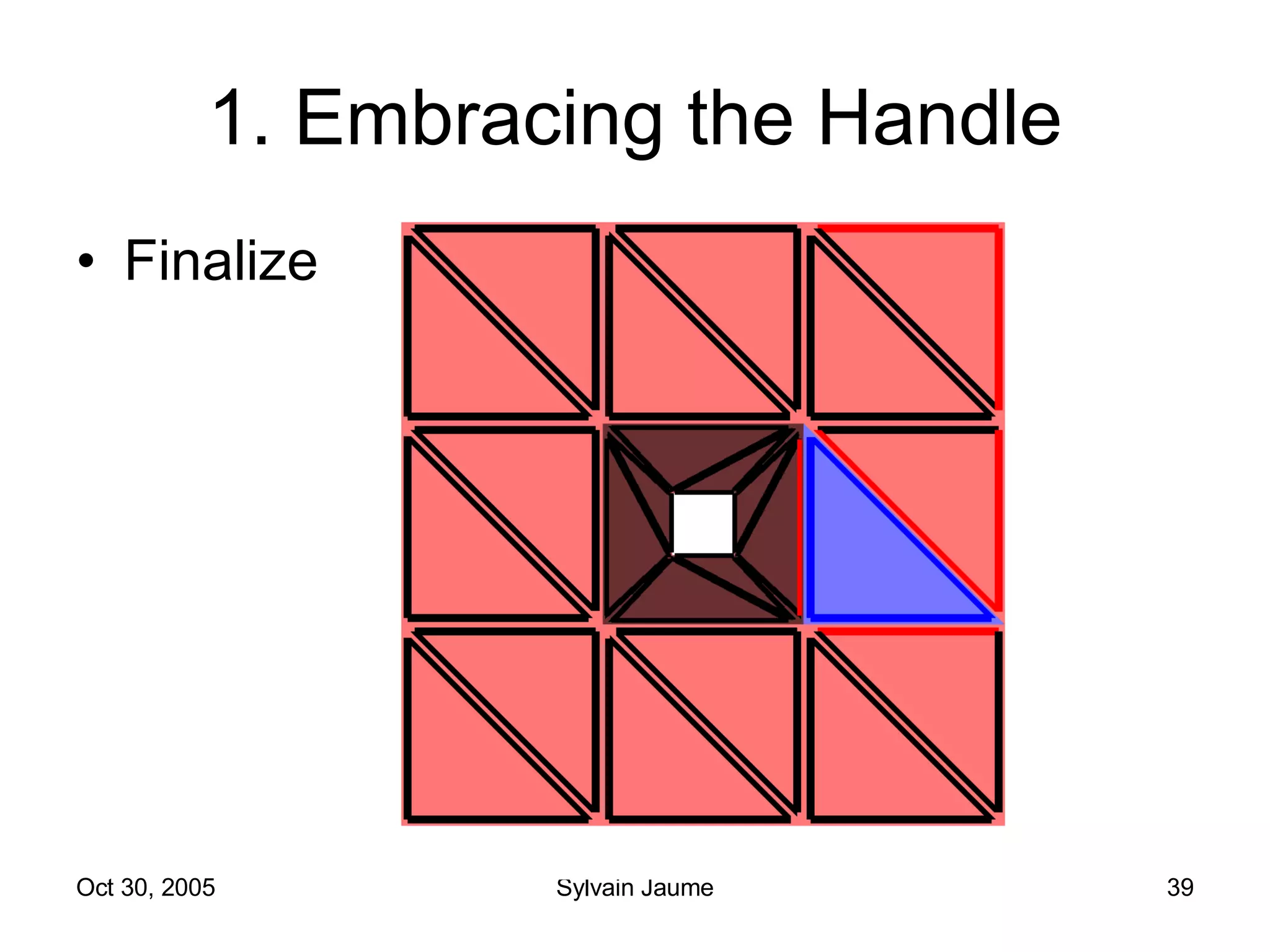
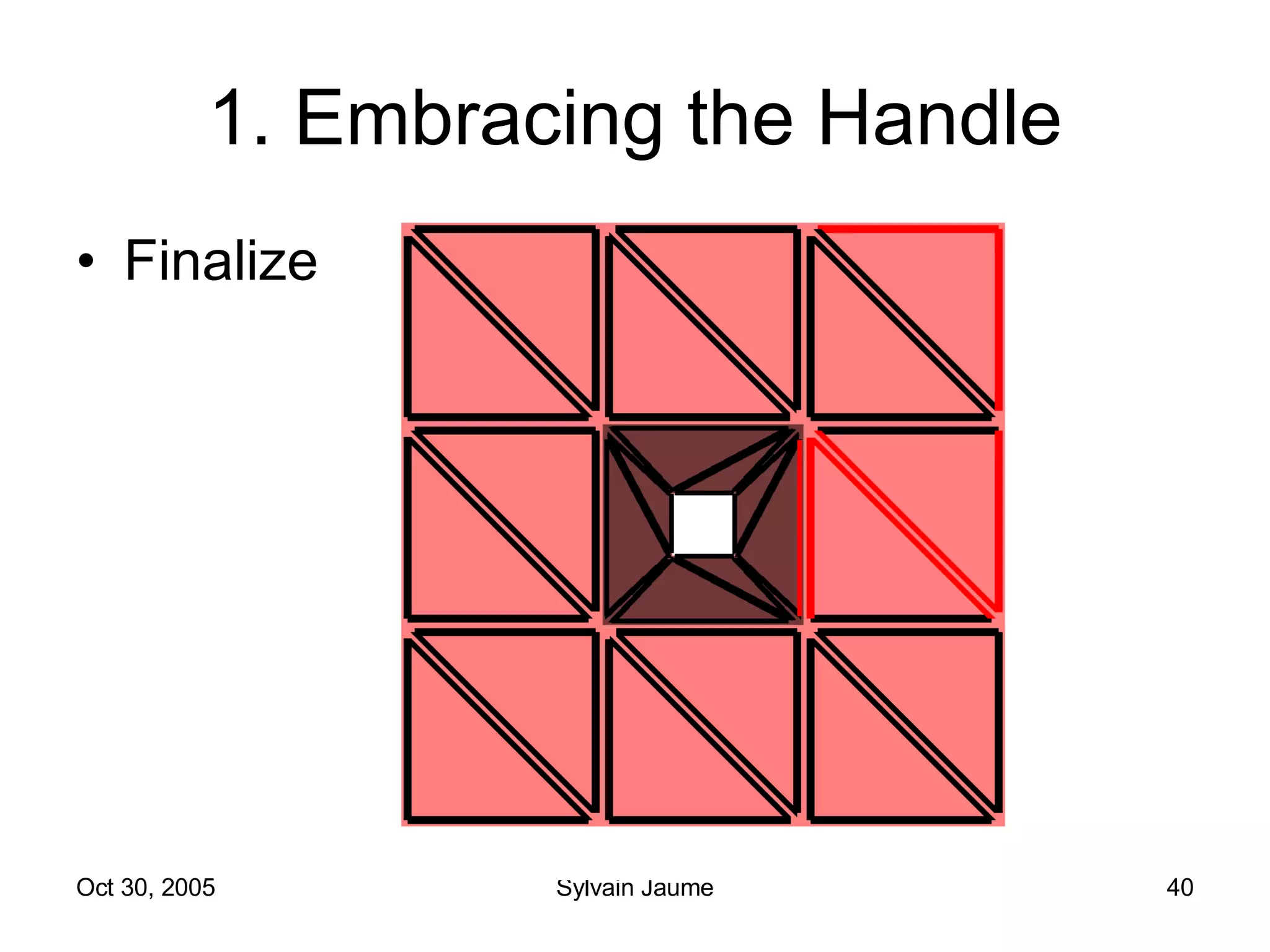
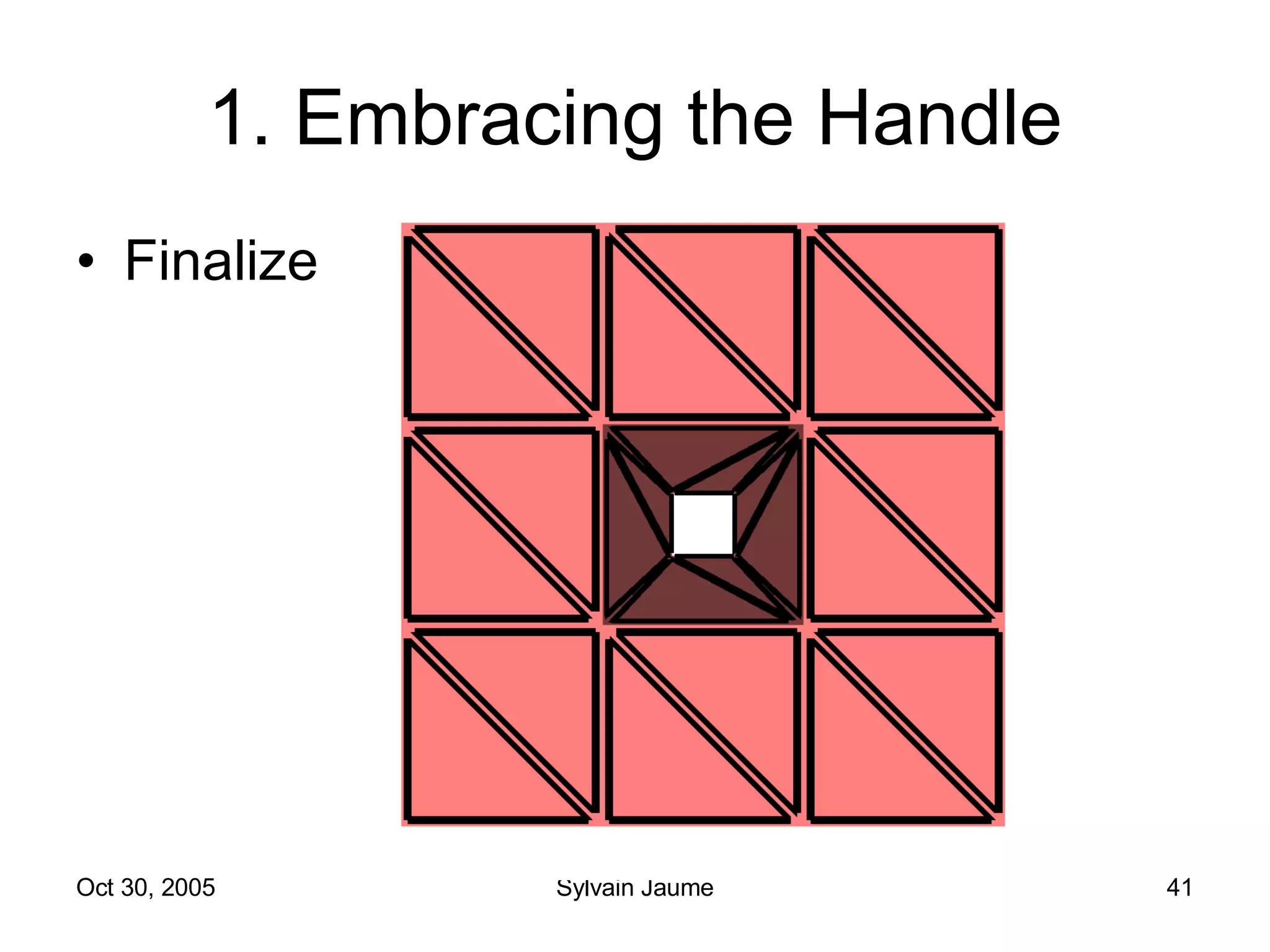
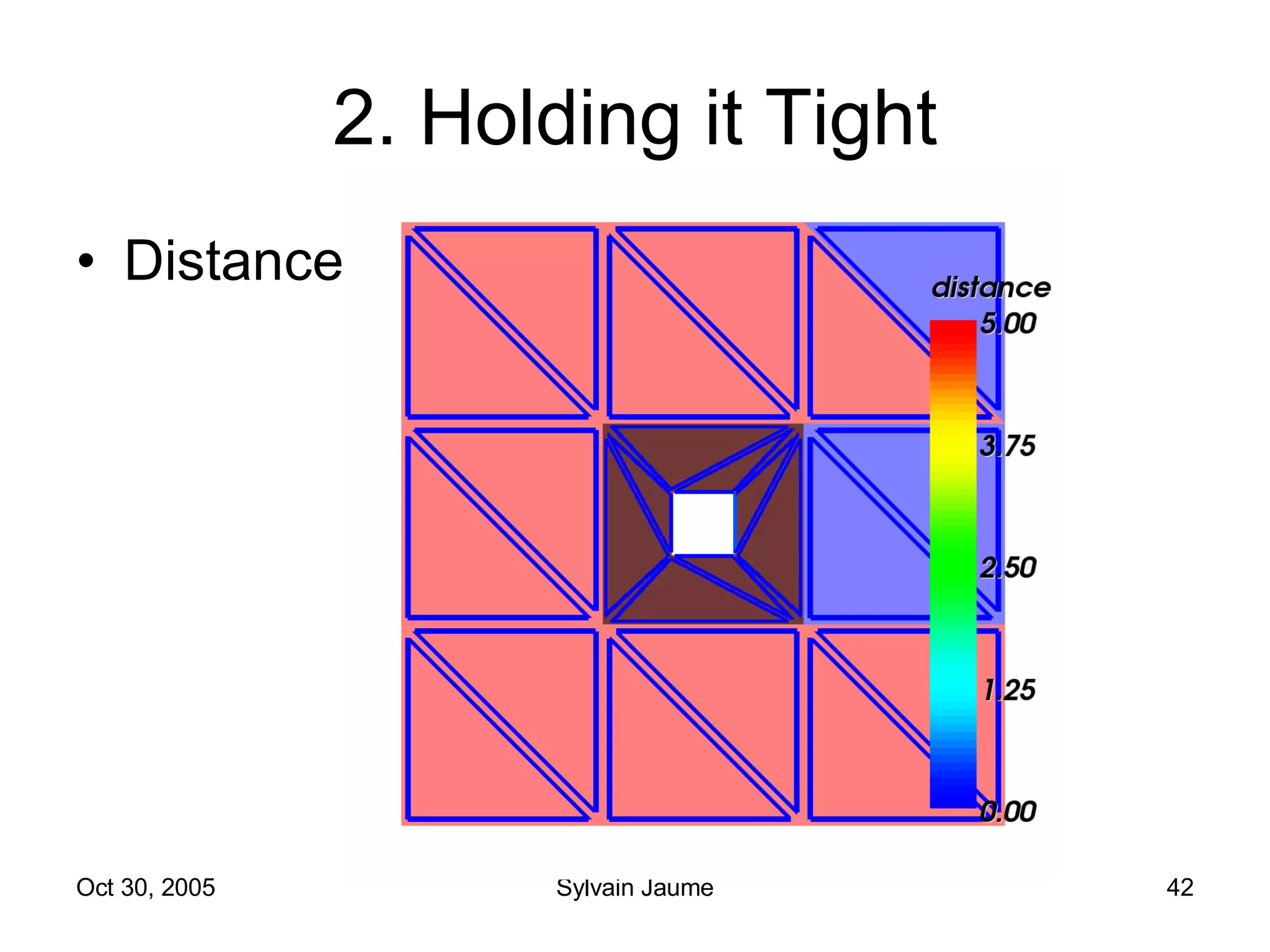
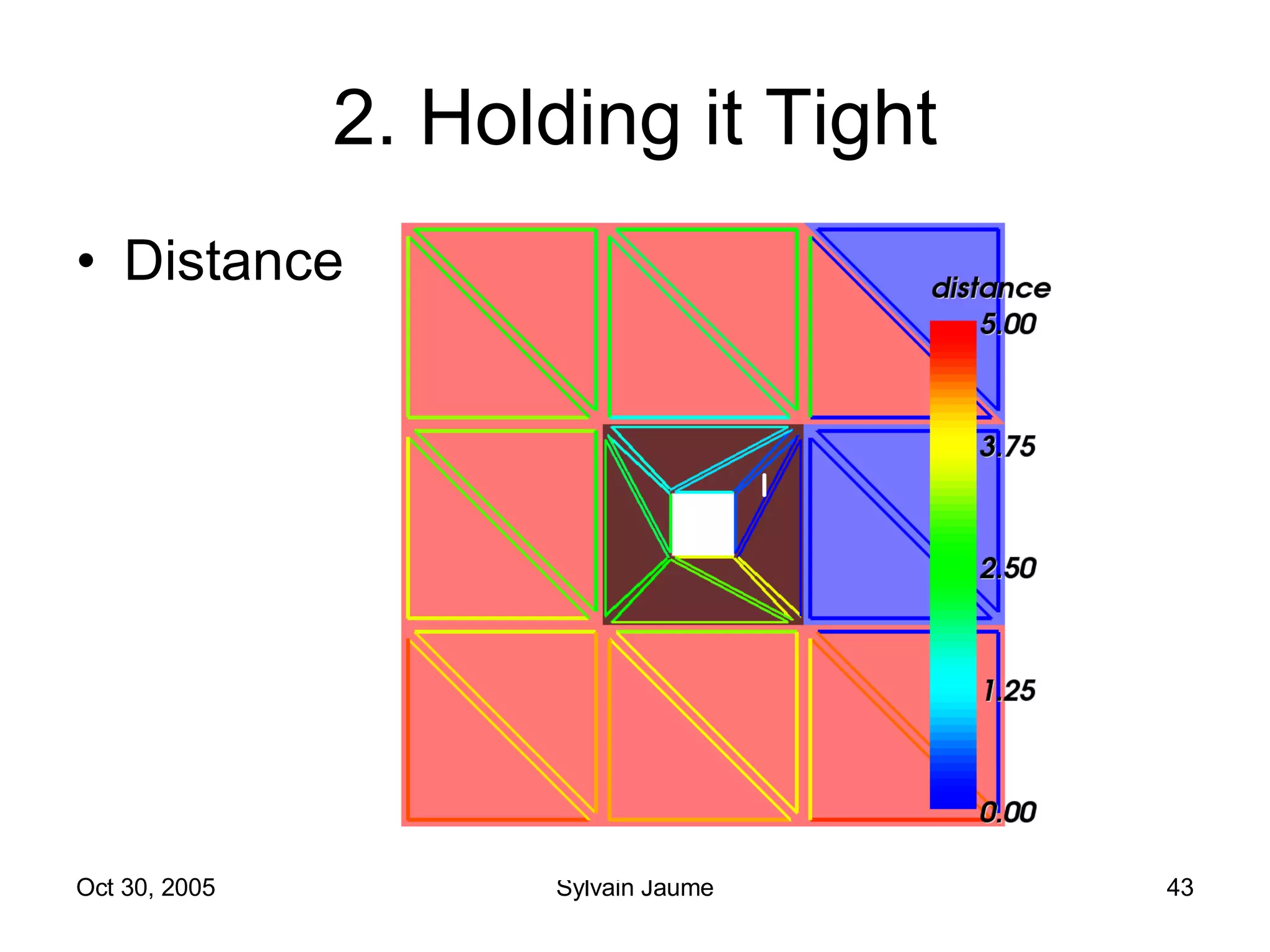
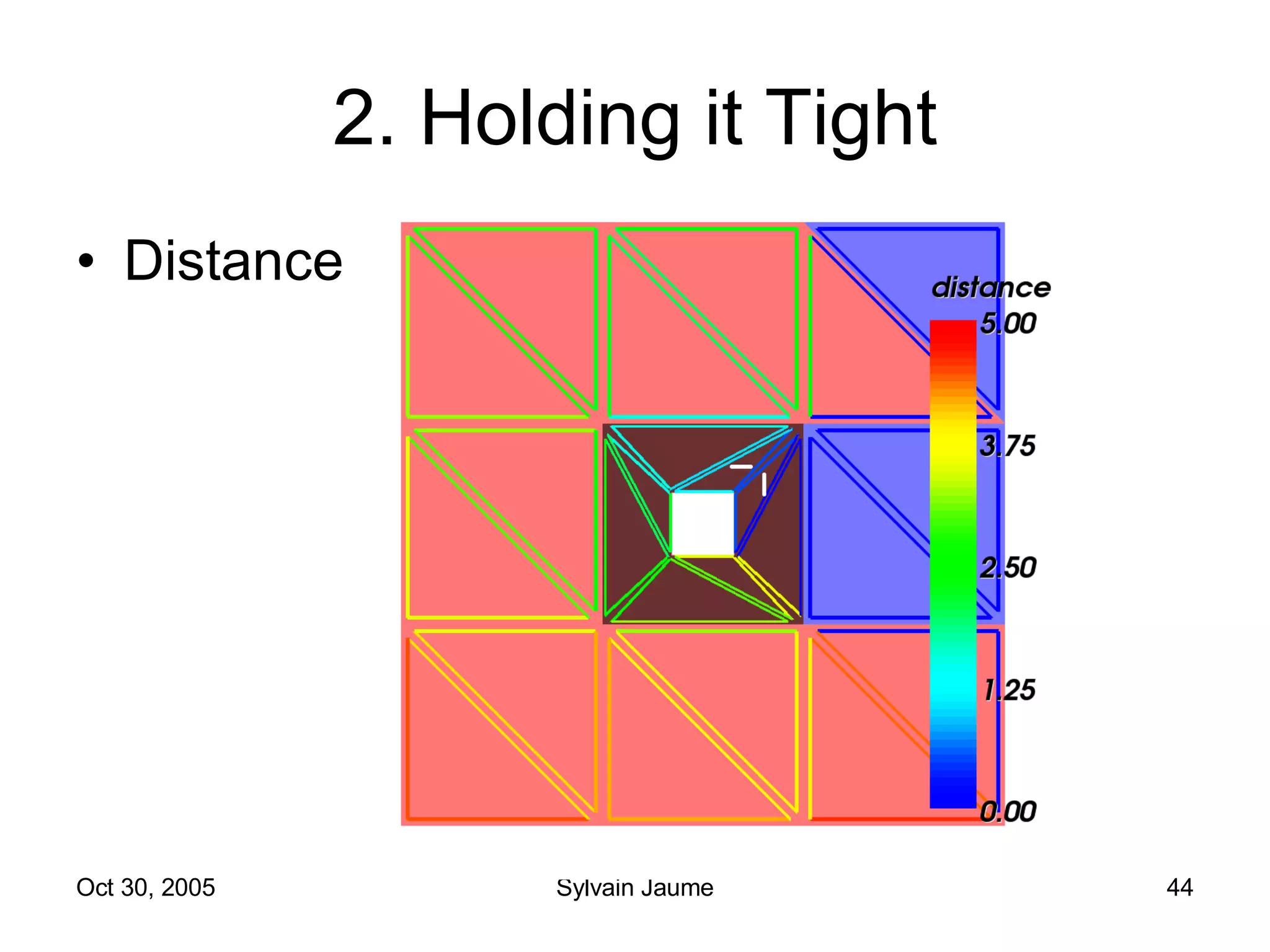
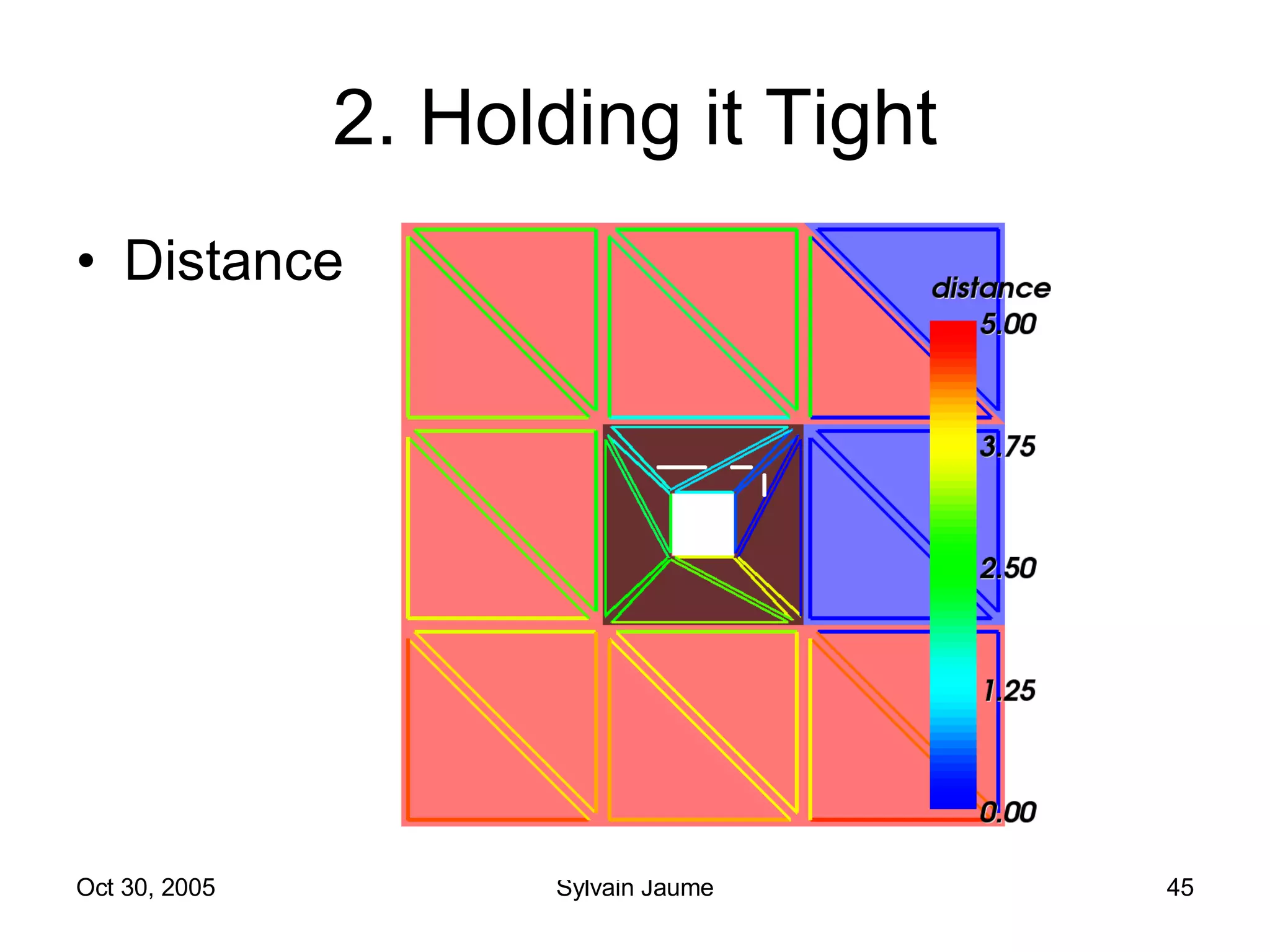
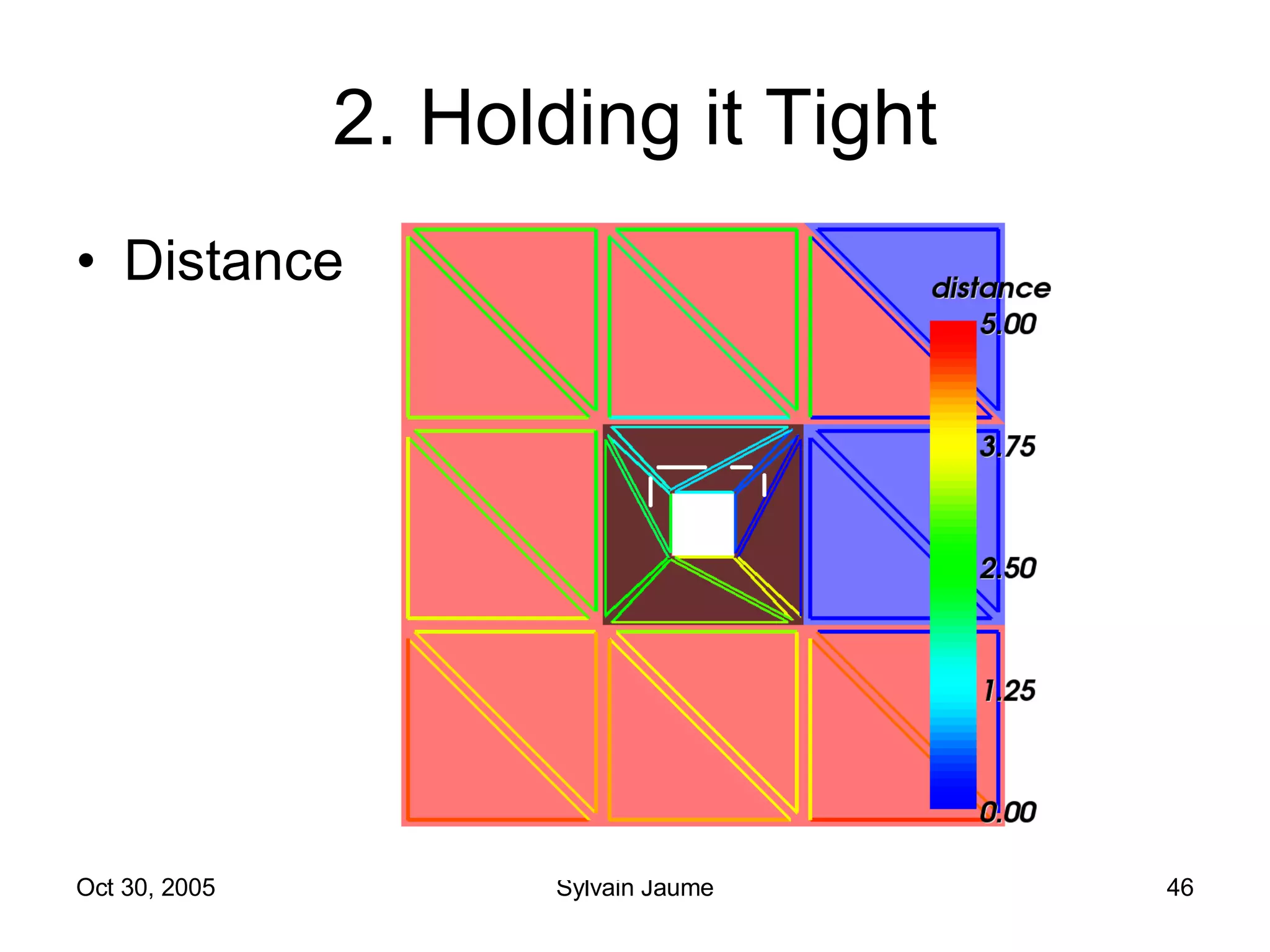
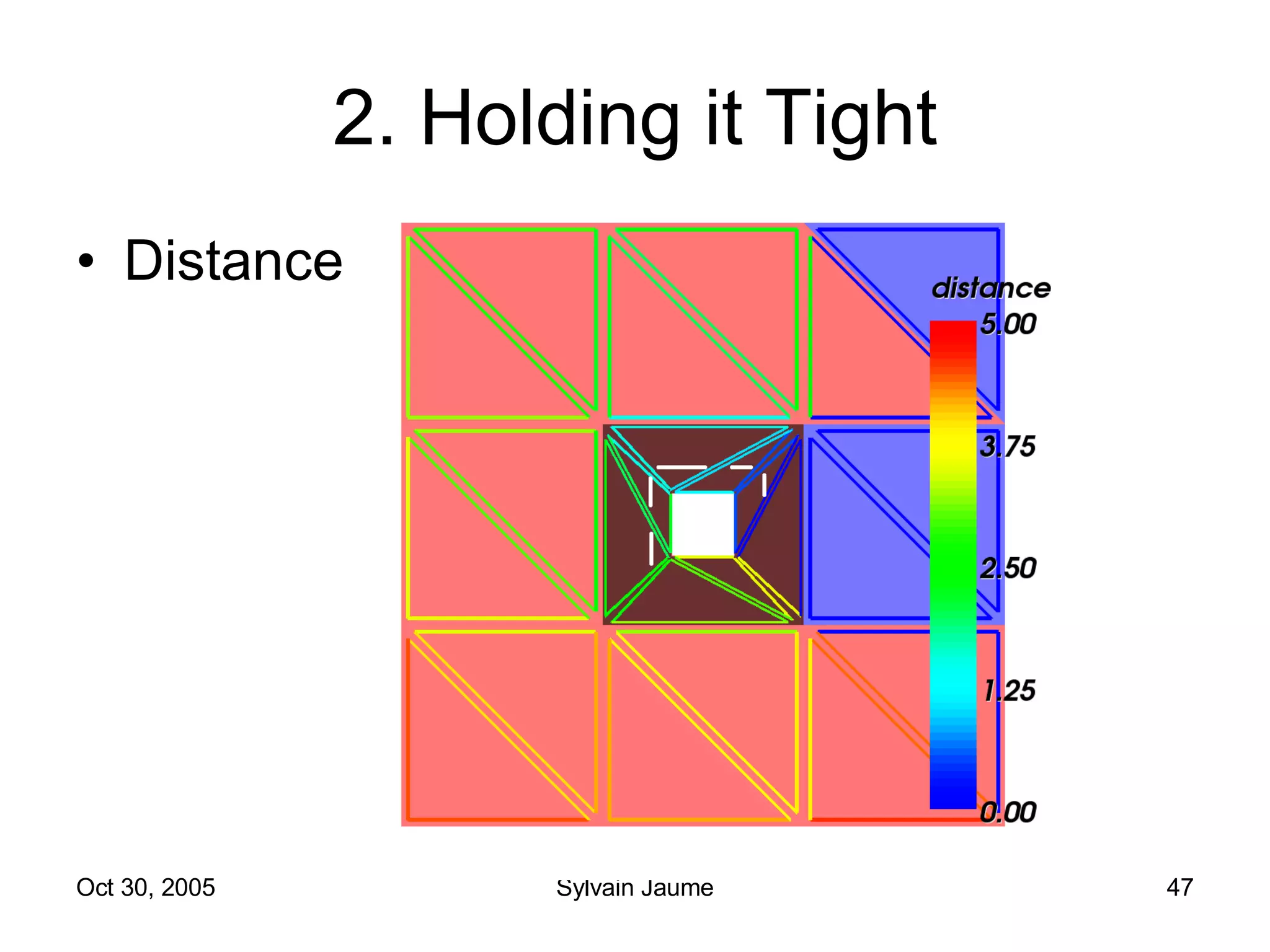
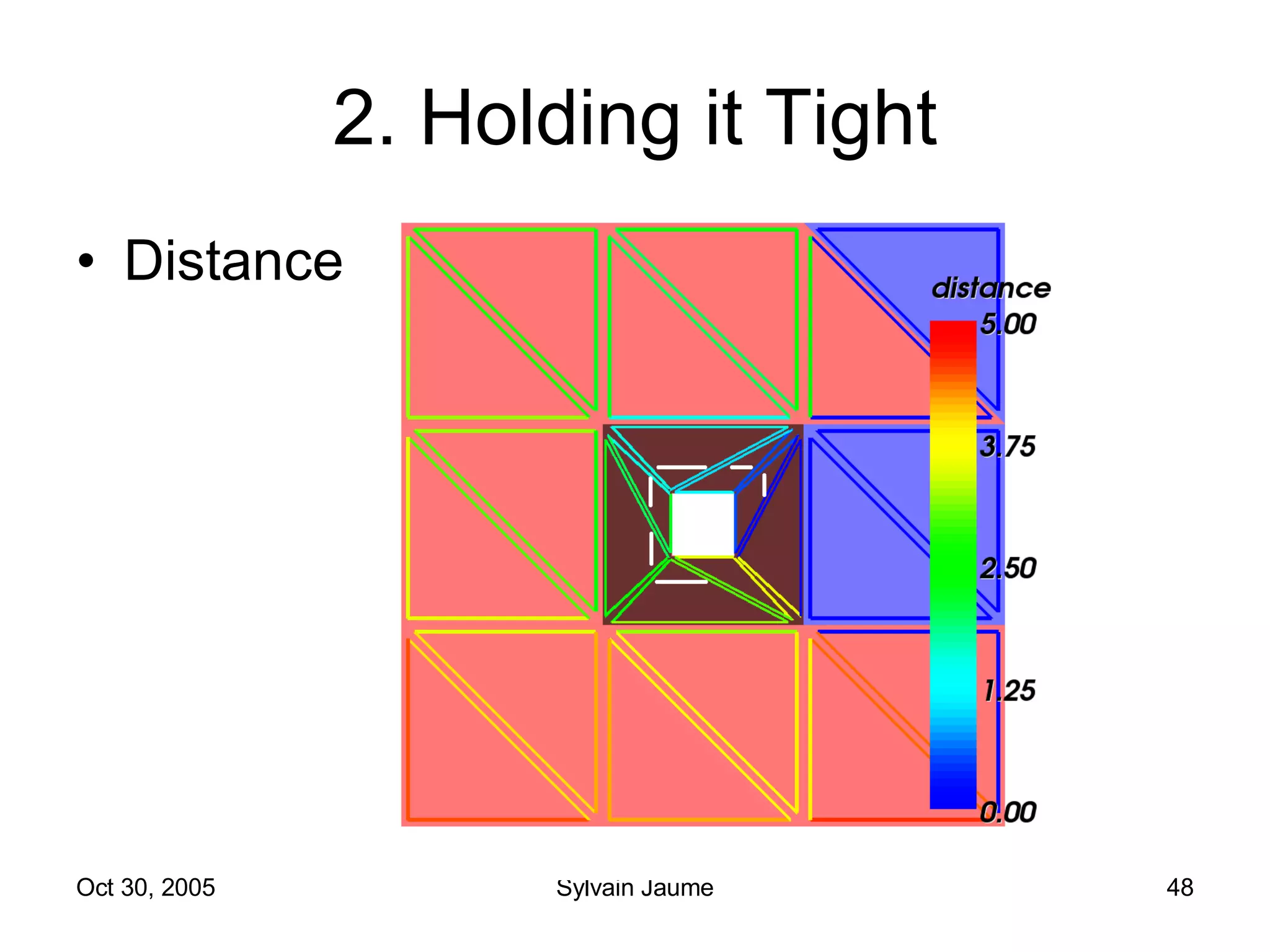
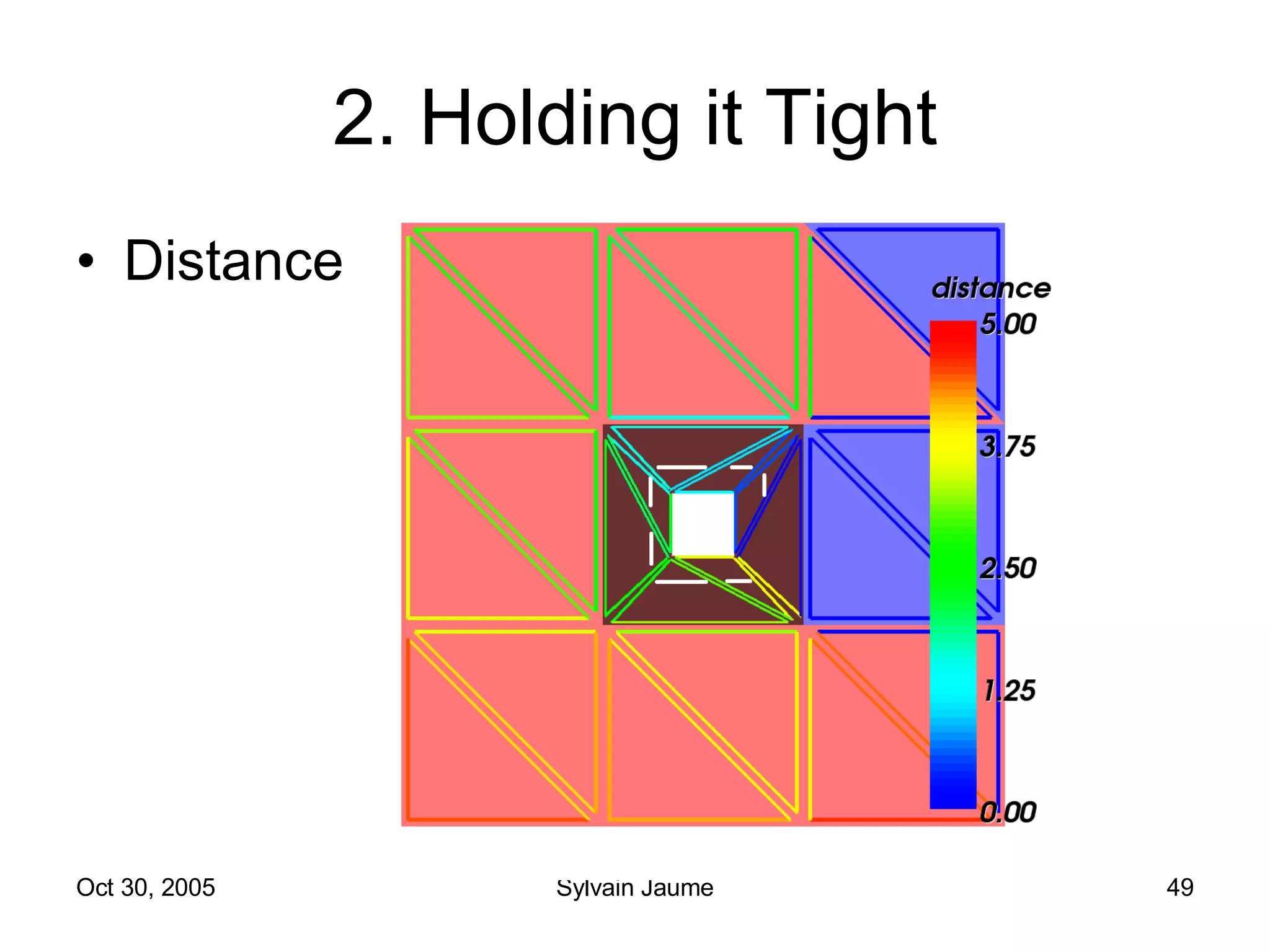
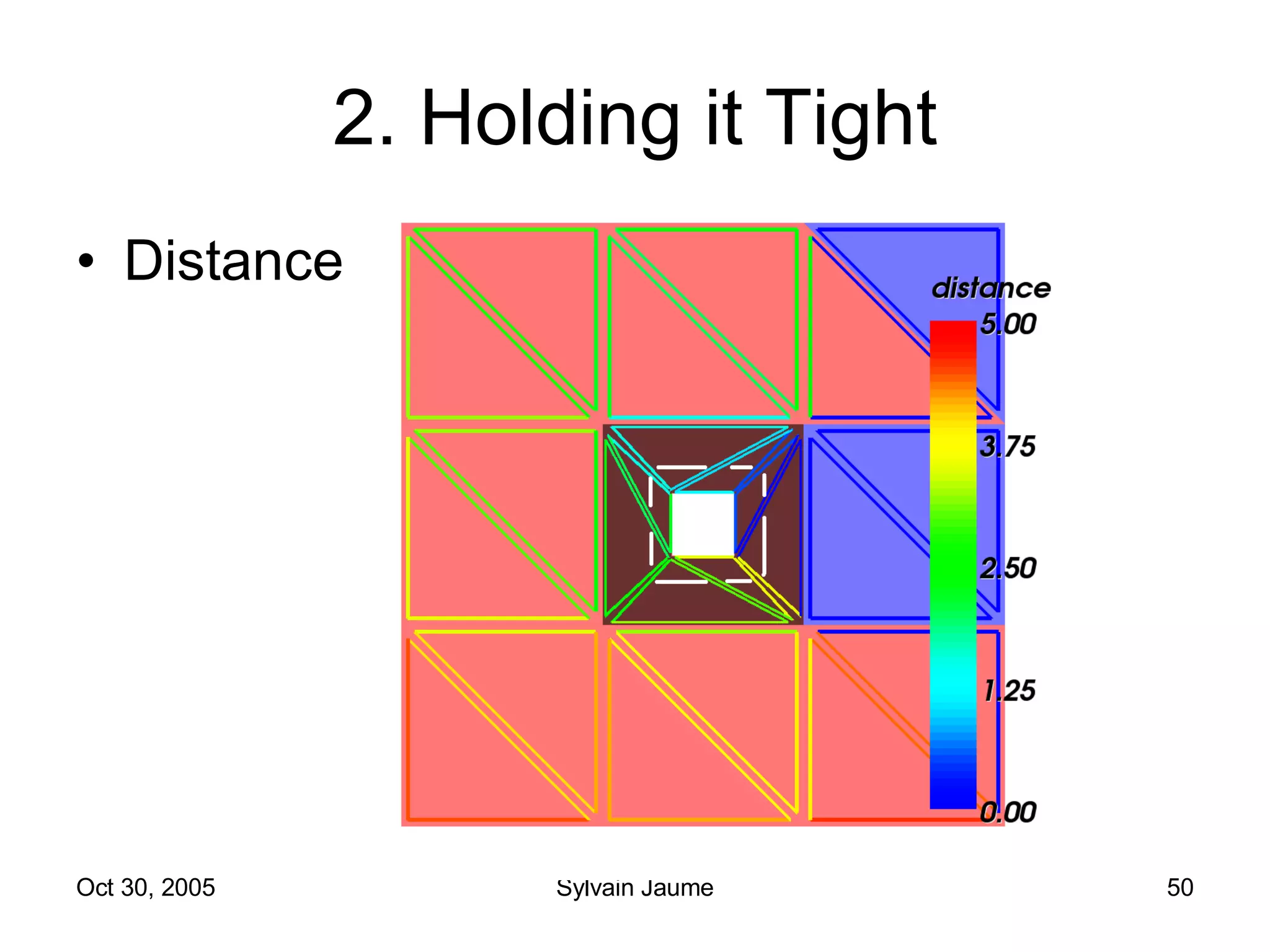
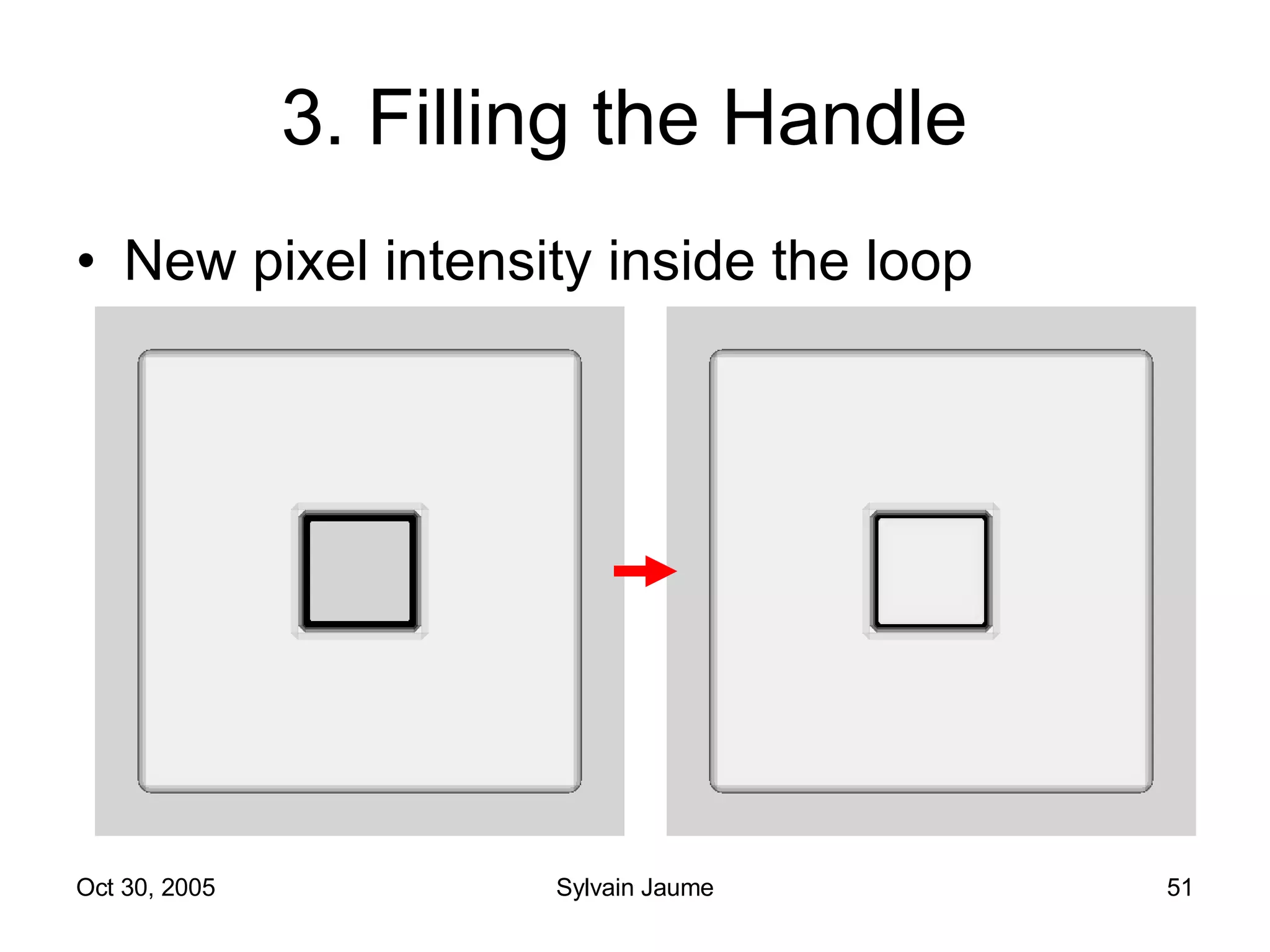
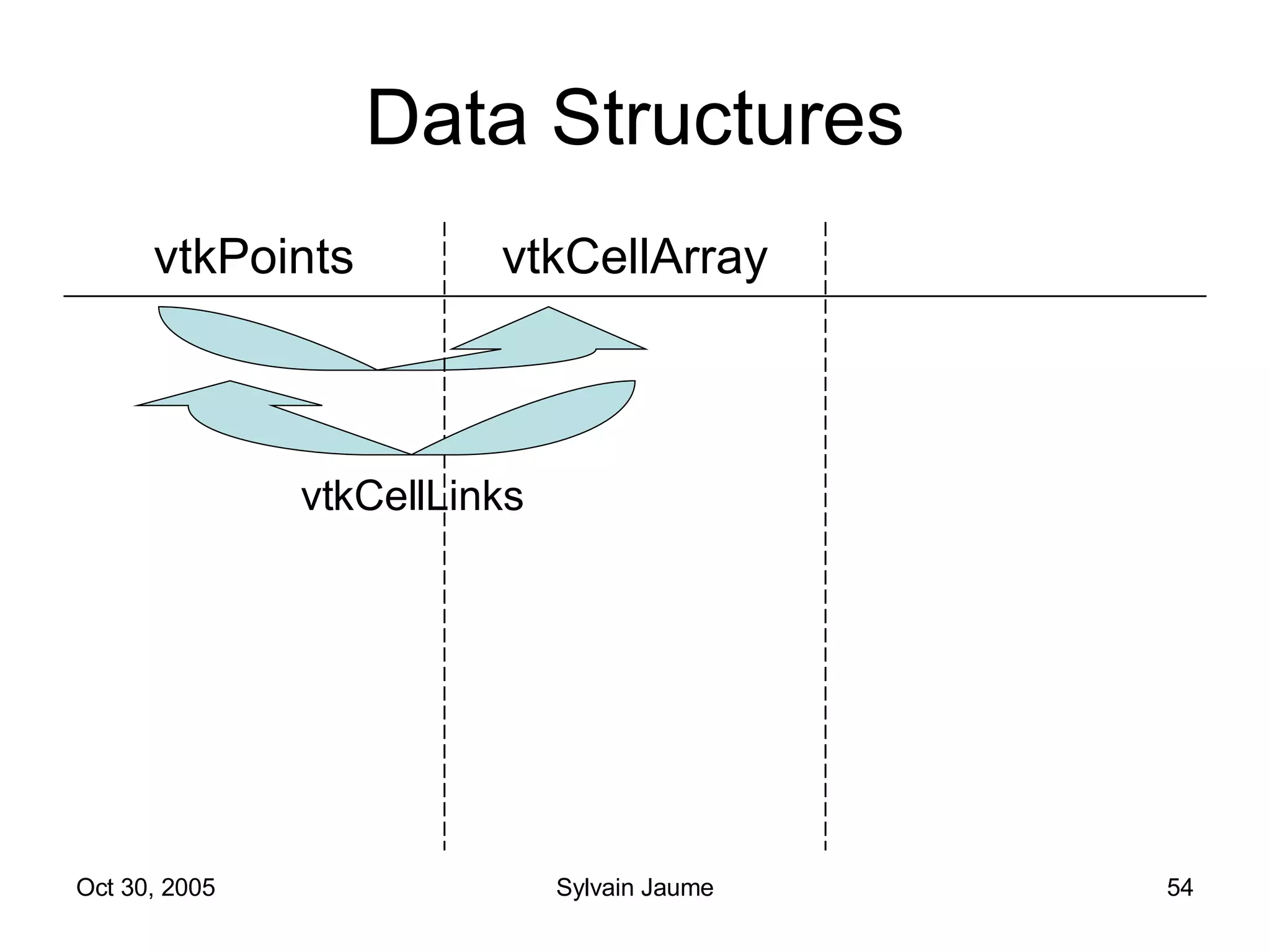
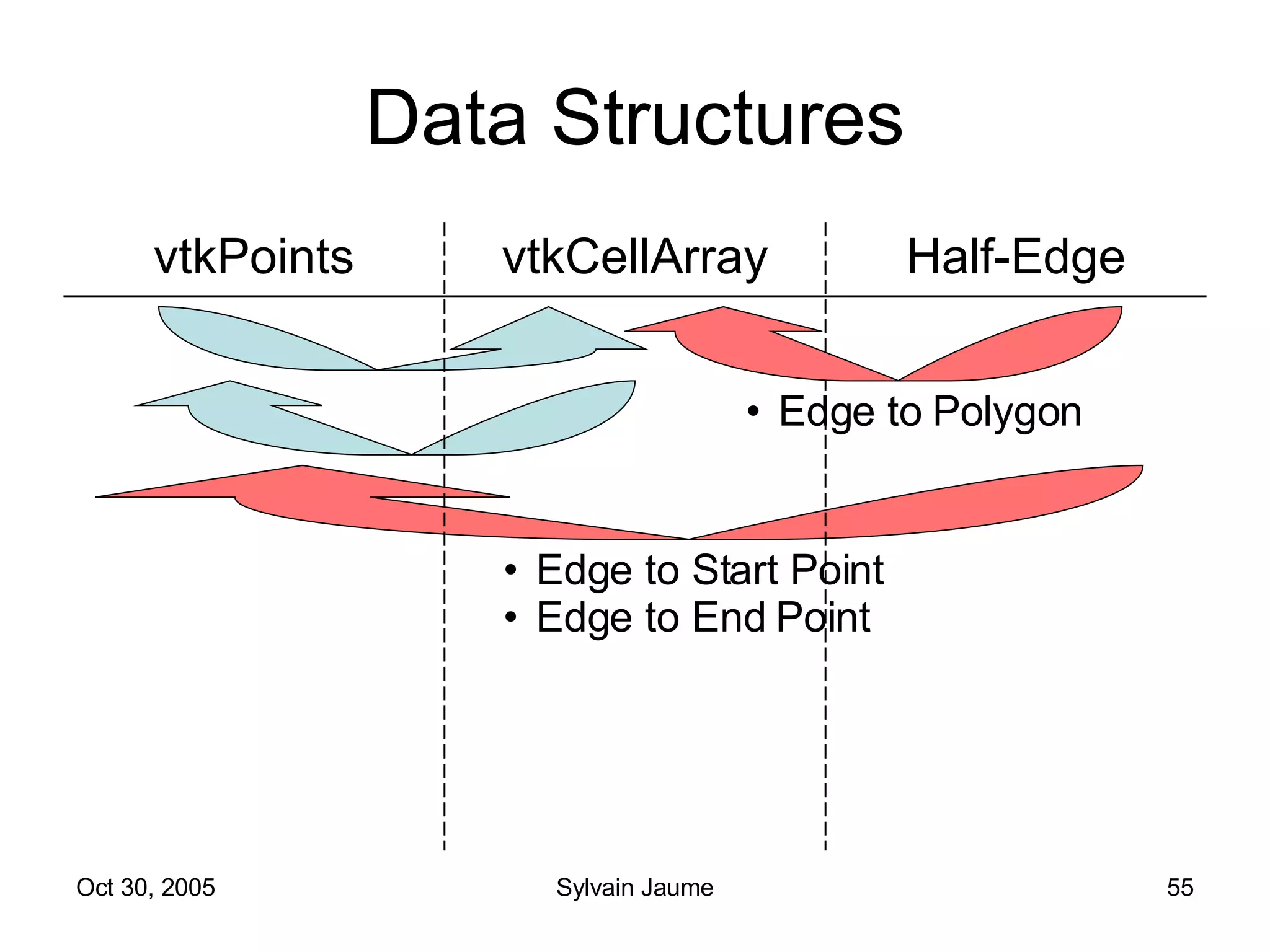
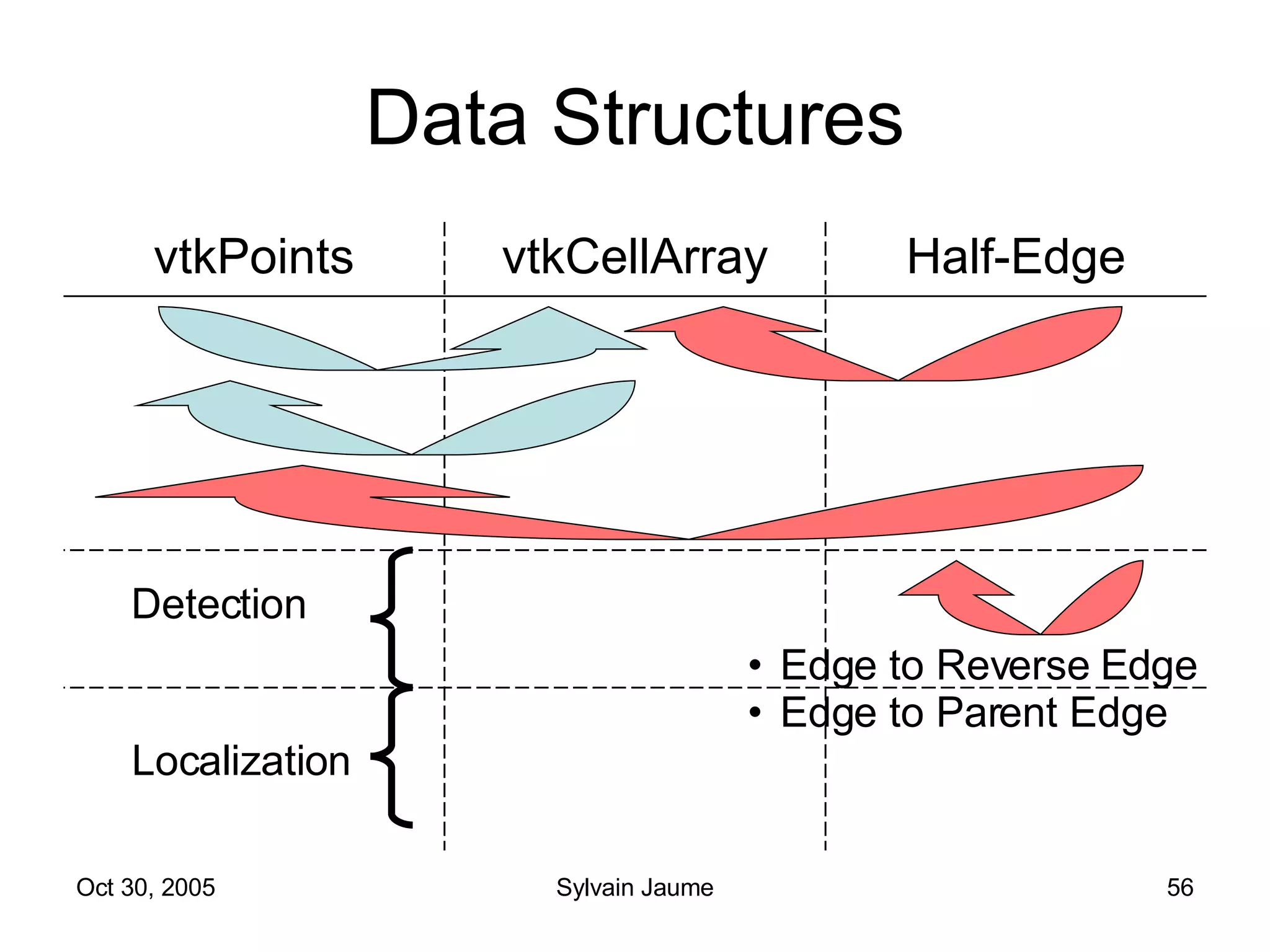
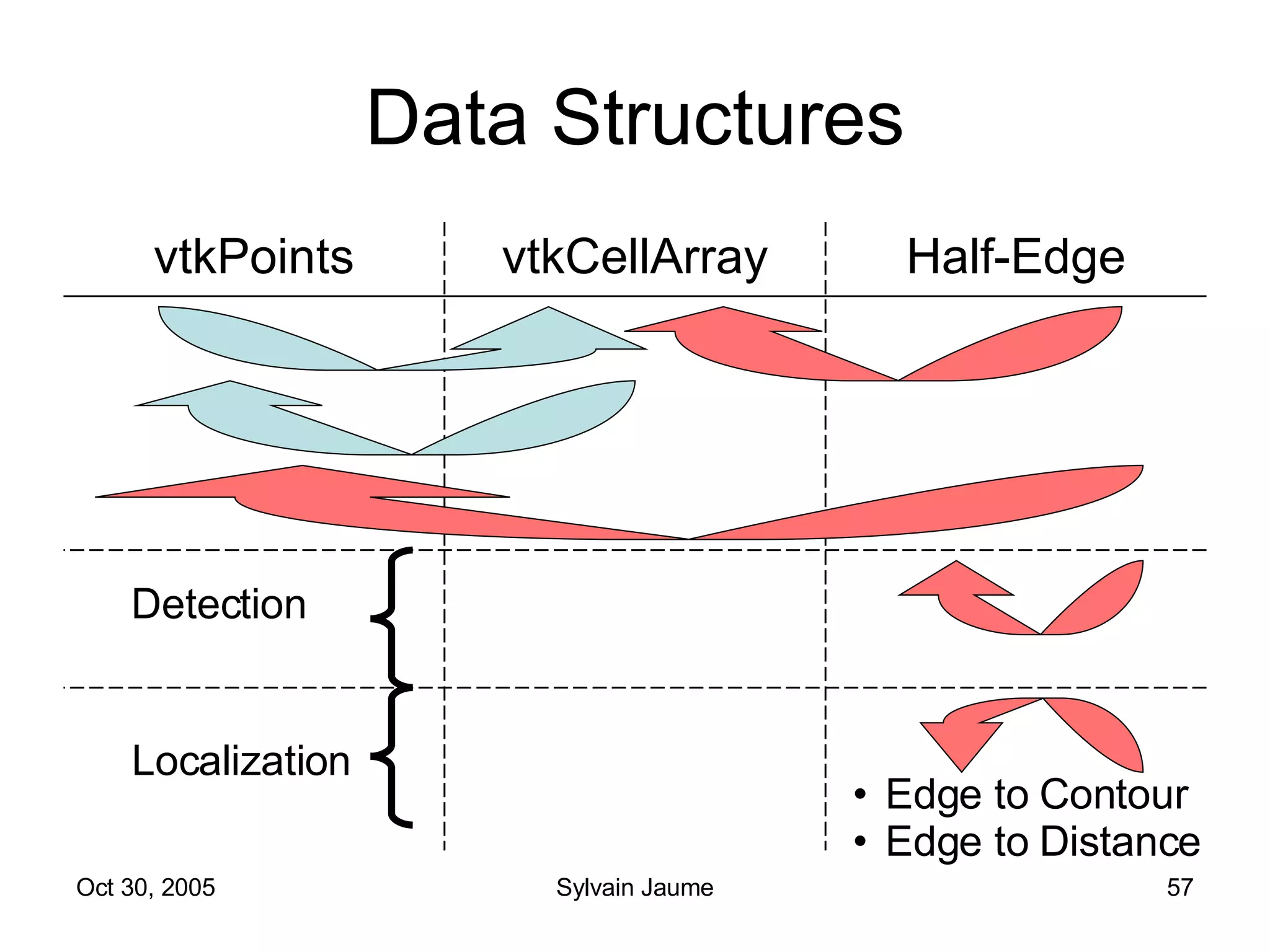
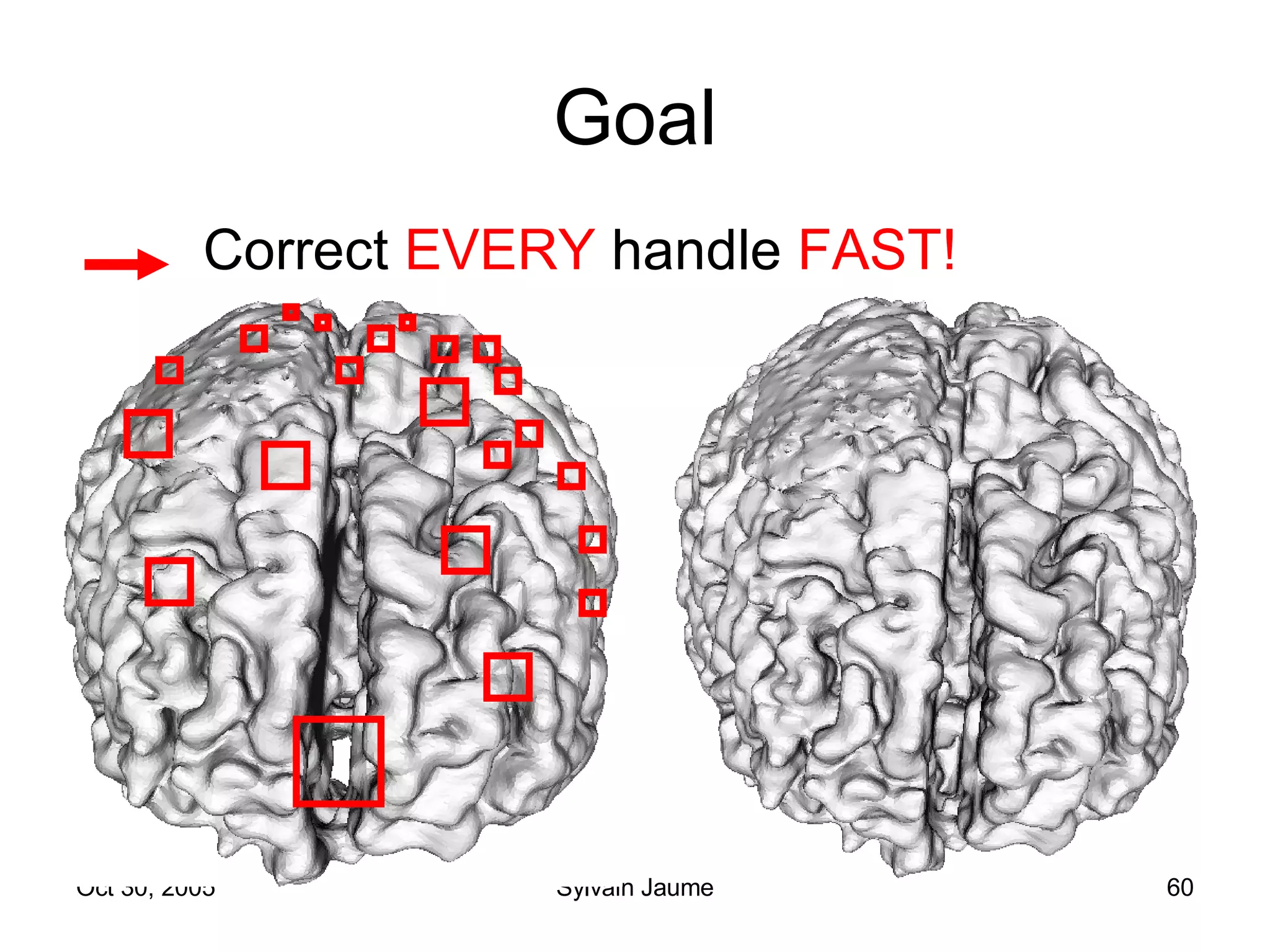
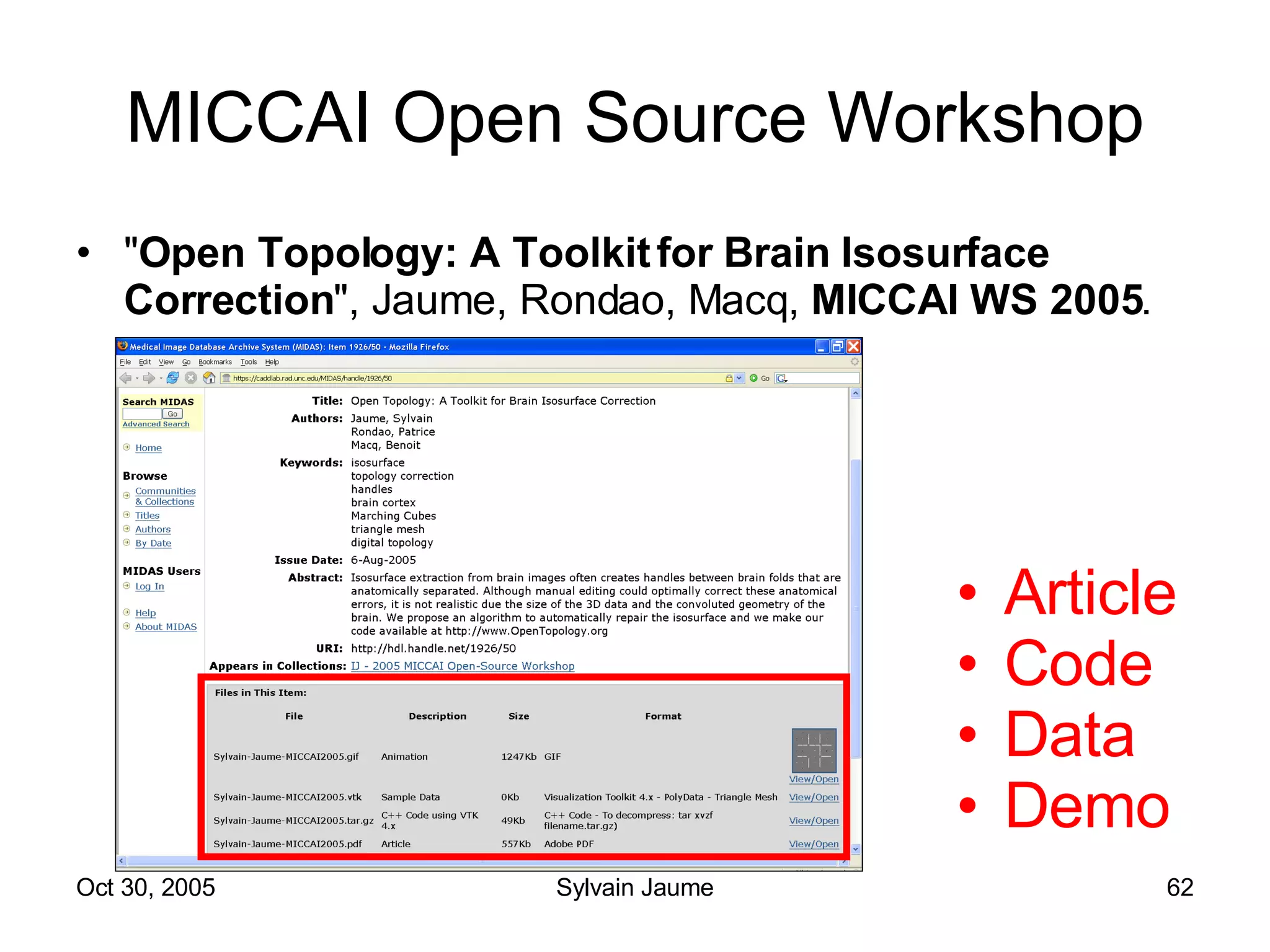
The document discusses Open Topology, a toolkit for correcting brain isosurface meshes extracted from MRI images. It describes how the toolkit uses a half-edge data structure and algorithms for handle detection, embracing handles, holding them tight, and filling handles to correct topological errors in the isosurfaces and generate watertight meshes. The toolkit aims to correctly handle all topological errors in brain isosurfaces rapidly and is open source.

1. Open Topology: A Toolkit for Brain Isosurface Correction Sylvain JAUME (1) , Patrice RONDAO (2) , Benoit MACQ (2) (1) Kitware Inc., (2) University of Louvain

2. Visualization of the Brain Speech, vision, etc. lie in the outer layer . surface visualization

3. Visualization of the Brain 3D Image Segmentation Marching Cubes Smoothing Mesh

4. Visualization of the Brain 3D Image Segmentation Marching Cubes Smoothing Mesh

5. Visualization of the Brain 3D Image Segmentation Marching Cubes Smoothing Mesh

6. Visualization of the Brain 3D Image Segmentation Marching Cubes Smoothing Mesh with Handles

7. Visualization of the Brain 3D Image Segmentation Marching Cubes Smoothing Mesh with Handles

8. Visualization of the Brain 3D Image Segmentation Marching Cubes Smoothing Mesh with Handles

9. Visualization of the Brain 3D Image Segmentation Marching Cubes Smoothing Mesh with Handles

10. Visualization of the Brain 3D Image Segmentation Marching Cubes Smoothing Mesh with Handles

11. Visualization of the Brain Where do handles come from ? Limited resolution Scanner artifacts Segmentation errors

12. Visualization of the Brain Does it really matter ??? For 3D visualization For distance measurements For EEG source localization

13. State of the Art Image methods Malandain 93, Shattuck 01, Kriegeskorte 01 Mesh methods Fischl 01, Guskov 01, Wood 04, Segonne 05 Graph methods Han 02, Segonne 03 Level-Set methods Han 01, Bischoff 02

14. Contributions No region is left out Fast (less than 2 min ) Open Source

15. Algorithm Overview Marching Cubes Handle Detection Handle Correction 3D Image Triangle Mesh Corrected 3D Image Contours

16. Algorithm Overview Marching Cubes Handle Detection Handle Correction 3D Image Triangle Mesh Contours Corrected 3D Image

17. Algorithm Overview Marching Cubes Handle Detection Handle Correction 3D Image Triangle Mesh Contours Corrected 3D Image

18. Algorithm Overview Marching Cubes Handle Detection Handle Correction 3D Image Triangle Mesh Polylines Corrected 3D Image

19. Algorithm Overview Marching Cubes Handle Detection Handle Correction 3D Image Triangle Mesh Contours Corrected 3D Image

20. Algorithm Overview Marching Cubes Handle Detection Handle Correction 3D Image Triangle Mesh Contours Corrected 3D Image

21. Algorithm Overview Marching Cubes Handle Detection Handle Correction 3D Image Triangle Mesh Contours Corrected 3D Image

22. Algorithm Overview Marching Cubes Handle Detection Handle Correction 3D Image Triangle Mesh Contours Marching Cubes Corrected Mesh Corrected 3D Image

23. Algorithm Overview Marching Cubes Handle Detection Handle Correction 3D Image Triangle Mesh Contours Marching Cubes Corrected Mesh Corrected 3D Image

24. Key Points 1. Embracing the Handle 2. Holding it Tight 3. Filling the Handle

25. 1. Embracing the Handle

26. 1. Embracing the Handle Init

27. 1. Embracing the Handle Init

28. 1. Embracing the Handle Init

29. 1. Embracing the Handle Init

30. 1. Embracing the Handle Split

31. 1. Embracing the Handle Split

32. 1. Embracing the Handle Split

33. 1. Embracing the Handle Merge

34. 1. Embracing the Handle Merge

35. 1. Embracing the Handle Merge

36. 1. Embracing the Handle Merge

37. 1. Embracing the Handle Merge

38. 1. Embracing the Handle Merge

39. 1. Embracing the Handle Finalize

40. 1. Embracing the Handle Finalize

41. 1. Embracing the Handle Finalize

42. 2. Holding it Tight Distance

43. 2. Holding it Tight Distance

44. 2. Holding it Tight Distance

45. 2. Holding it Tight Distance

46. 2. Holding it Tight Distance

47. 2. Holding it Tight Distance

48. 2. Holding it Tight Distance

49. 2. Holding it Tight Distance

50. 2. Holding it Tight Distance

51. 3. Filling the Handle New pixel intensity inside the loop

52. Putting it Together Handle Detection Embracing the handle Handle Localization Holding it tight Handle Correction Filling the handle

53. Performance g: genus, i.e. number of handles V: number of vertices E: number of edges F: number of faces C: number of connected components Euler Characteristic

54. Data Structures vtkCellLinks vtkCellArray vtkPoints

55. Data Structures Edge to Start Point Edge to End Point Edge to Polygon Half-Edge vtkCellArray vtkPoints

56. Data Structures Edge to Reverse Edge Edge to Parent Edge Detection Localization Half-Edge vtkCellArray vtkPoints

57. Data Structures Edge to Contour Edge to Distance Detection Localization Half-Edge vtkCellArray vtkPoints

58. Data Structures Extended Half-Edge Structure: Edge to Polygon Edge to Start Point Edge to End Point Edge to Reverse Edge Edge to Parent Edge Edge to Contour Edge to Distance

59. Code vtkHandleDetection Half-edge structure Area growing Shortest loop vtkHandleCorrection Loop to image Water-tight region

60. Goal Correct EVERY handle FAST!

61. Perspectives Visualization, measurements, source localization Benchmarking with other methods Half-Edge algorithms Integration into CARET Software

62. MICCAI Open Source Workshop " Open Topology: A Toolkit for Brain Isosurface Correction ", Jaume, Rondao, Macq, MICCAI WS 2005 . Article Code Data Demo

63. www.OpenTopology.org Algorithm Source code Documentation Data Updates

64. Acknowledgements Special thanks to M. Ferrant, S.K. Warfield, A.H. Barr, and many others at UCL-Belgium, CalTech, SPL, MIT, INRIA and VTK mailing list. Thank you for your interest!

65. References I Segonne, Florent and Grimson, W. Eric L and Fischl, Bruce, A Genetic Algorithm for the Topology Correction of Cortical Surfaces, IPMI 2005. Bischoff, Stefan and Kobbelt, Leif, Sub-Voxel Topology Control for Level-Set Surfaces},Computer Graphics Forum 2003. Stephan Bischoff, Leif Kobbelt, Parameterization-free active contour models with topology control, The Visual Computer 2004. Aktouf, Zouina and Bertrand, Gilles and Perroton, Laurent, A three-dimensional holes closing algorithm, Pattern Recognition Letters 2002. Bertrand, Gilles, Simple Points, topological numbers and geodesic neighborhood in cubic grids, Pattern Recognition Letters 1994. Bertrand, Gilles, A boolean characterization of three-dimensional simple points, Pattern Recognition Letters 1996. G. Bertrand and G. Malandain, A New Characterization of Three-Dimensional Simple Points, Pattern Recognition Letters 1994

66. References II Fischl, B. and Liu, A. and Dale, A. M., Automated Manifold Surgery: Constructing Geometrically Accurate and Topologically Correct Models of the Human Cerebral Cortex, IEEE Transactions on Medical Imaging. Han, X., Xu, C., Braga-Neto, U., Prince, J., Topology Correction in Brain Cortex Segmentation Using a Multiscale Graph-based Algorithm, IEEE Transactions on Medical Imaging 2002. X. Han, C. Xu, D. Tosun, and J. L. Prince, Cortical Surface Reconstruction Using a Topology Preserving Geometric Deformable Model, MMBIA 2001. Kriegeskorte, N. and Goebel, R., An Efficient Algorithm for Topologically Correct Segmentation of the Cortical Sheet in Anatomical MR Volumes, NeuroImage, 2001. Shattuck, D. W. and Leahy, R. M., Automated Graph-based Analysis and Correction of Cortical Volume Topology, IEEE Transactions on Medical Imaging, 2001. Bischoff, S. and Kobbelt, L., Isosurface Reconstruction with Topology Control, Pacific Graphics Proceedings, 2002.

67. References III Bischoff, Stephan and Kobbelt, Leif, Topologically Correct Extraction of the Cortical Surface of a Brain Using Level-Set Methods, Bildverarbeitung fuer die Medizin, 2004. Malandain, Grégoire and Bertrand, Gilles and Ayache, Nicholas, Topological Segmentation of Discrete Surfaces, International Journal of Computer Vision, 1993. Zeng, X. and Staib, L. H. and Schultz, R. T. and Duncan, J. S., Segmentation and Measurement of the Cortex from 3D MR Images Using Coupled Surfaces Propagation, IEEE Transactions on Medical Imaging, 1999. Ségonne, F. and Fischl, B. and Grimson, E., Topology correction of Subcortical Structures, Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2003. Guskov, I. and Wood, Z., Topological Noise Removal, Graphics Interface, 2001. Wood, Z. J. and Hoppe, H. and Desbrun, M. and Schröder, P., Removing Excess Topology from Isosurfaces, ACM Transactions on Graphics, 2004.

68. State of the Art Image methods Can miss large regions Mesh methods Self-intersections Graph methods Computationally intensive Level-Set methods Controlled with heuristics