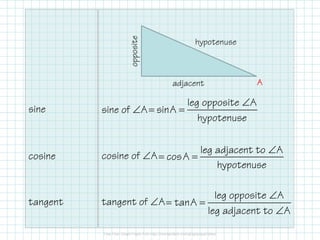
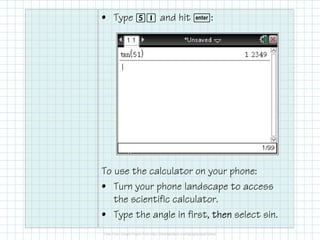
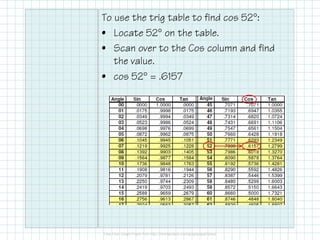
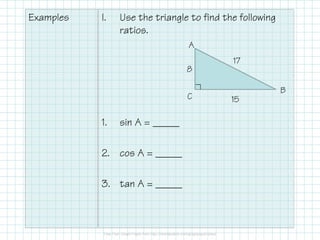
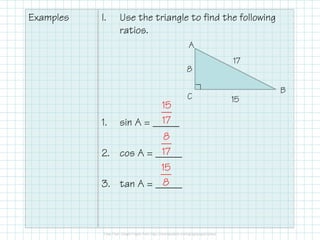
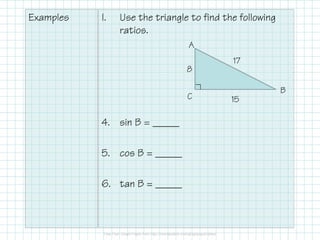
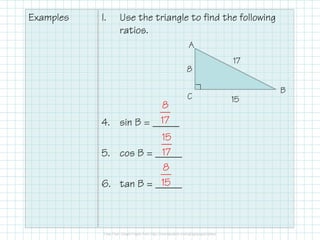
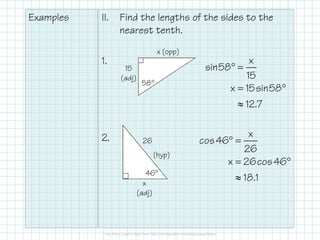
The document covers foundational concepts in trigonometry, focusing on the definitions and application of sine, cosine, and tangent ratios as well as their inverses. It explains how to solve for missing sides or angles in right triangles using either calculators or trig tables, emphasizing the importance of memorizing these ratios along with mnemonic aids. Additionally, it provides examples to demonstrate how to calculate these ratios and solve related problems.

1. Obj. 40 Trigonometry
The student is able to (I can):
For any right triangle
• Define the sine, cosine, and tangent ratios and their
inverses
• Find the measure of a side given a side and an angle
• Find the measure of an angle given two sides
• Use trig ratios to solve problems

2. By the Angle-Angle Similarity Theorem, a
right triangle with a given acute angle is
similar to every other right triangle with the
same acute angle measure. This means
that the ratios between the sides of those
triangles are always the same.
Because these ratios are so useful, they
were given names: sine cosine and
sine, cosine,
tangent.
tangent These ratios are used in the
study of trigonometry.

3. opposite
hypotenuse
adjacent
A
sine
leg opposite ∠A
sine of ∠A = sinA =
hypotenuse
cosine
cosine of ∠A = cosA =
tangent
leg opposite ∠A
tangent of ∠A = tanA =
leg adjacent to ∠A
leg adjacent to ∠A
hypotenuse

4. We can use the trig ratios to find either
missing sides or missing angles of right
triangles. To do this, we will set up
equations and solve for the missing part.
In order to figure out the sine, cosine, and
tangent ratios, we can use either a
calculator or a trig table.

5. To use the calculator to find tan 51°:
• From a New Document, press the µ key:
• Use the right arrow key ( ) to select tan
(¢)
and press ·:

6. • Type 5I and hit ·:
To use the calculator on your phone:
• Turn your phone landscape to access
the scientific calculator.
• Type the angle in first, then select sin.

7. To use the trig table to find cos 52°:
• Locate 52° on the table.
• Scan over to the Cos column and find
the value.
• cos 52° = .6157

8. You will be expected to memorize these
ratios. There are many hints out there to
help you keep them straight. The most
common is SOH-CAH-TOA , where
SOH-CAHOp p
Sin =
Hyp
Adj
Cos =
Hyp
Op p
Tan =
Adj
A mnemonic I like is “Some Old Hippie
Caught Another Hippie Trippin’ On Acid.”
Or “Silly Old Hitler Couldn’t Advance His
Troops Over Africa.”

9. Examples
I.
Use the triangle to find the following
ratios.
A
8
C
1.
sin A = _____
2. cos A = _____
3. tan A = _____
17
B
15

10. Examples
I.
Use the triangle to find the following
ratios.
A
8
1.
15
17
sin A = _____
8
17
2. cos A = _____
15
8
3. tan A = _____
C
17
B
15

11. Examples
I.
Use the triangle to find the following
ratios.
A
8
C
4. sin B = _____
5. cos B = _____
6. tan B = _____
17
B
15

12. Examples
I.
Use the triangle to find the following
ratios.
A
8
8
17
4. sin B = _____
15
17
5. cos B = _____
8
15
6. tan B = _____
C
17
B
15

13. Examples
II.
Find the lengths of the sides to the
nearest tenth.
x (opp)
1.
15
(adj)
58°
x
sin58° =
15
x = 15sin58°
≈ 12.7
2.
x
26
x = 26cos 46°
cos 46° =
26
(hyp)
46°
x
(adj)
≈ 18.1