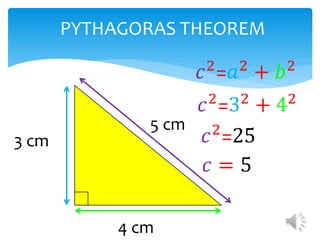
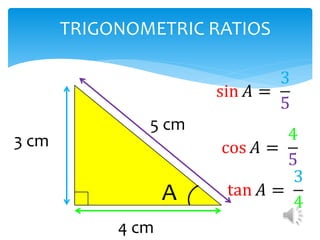
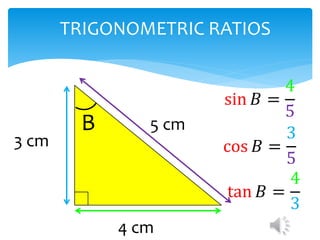
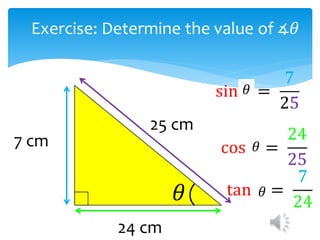
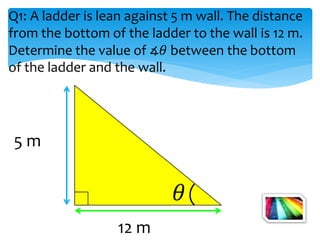
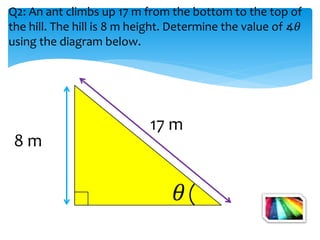
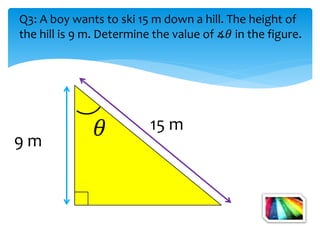
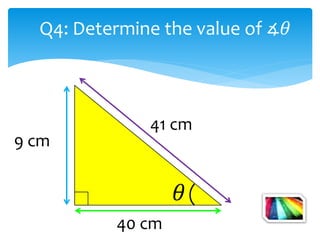
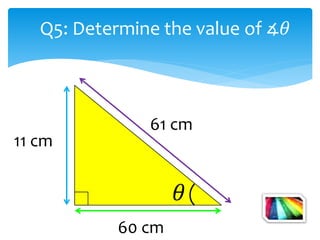
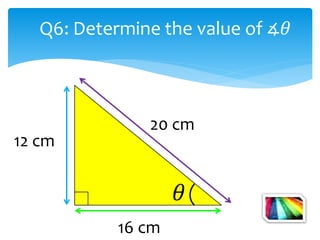
This document introduces the SOH CAH TOA mnemonic for remembering the definitions of the trigonometric ratios sine, cosine, and tangent. It states that SOH CAH TOA is a trigonometric ratio and defines sine as opposite over hypotenuse, cosine as adjacent over hypotenuse, and tangent as opposite over adjacent. It then provides examples of using trigonometric ratios to solve for unknown angles and sides of right triangles.

1. SOH CAH TOA SONG
SOH CAH TOA is a trigonometric ratio
SOH CAH TOA ooo..
and SOH is sin 𝜃 equal to
opposite over hypotenuse
SOH CAH TOA is a trigonometric ratio
SOH CAH TOA ooo..
and CAH is cah 𝜃 equal to
adjacent over hypotenuse
SOH CAH TOA is a trigonometric ratio
SOH CAH TOA ooo..
and TOA is tan 𝜃 equal to
opposite over adjacent

2. CHAPTER: TRIGONOMETRY
SUB TOPIC: TRIGONOMETRIC RATIOS

3.  At the end of the lesson, students should be able to:
 1. Use the previous knowledge of Pythagoras
Theorem to find sides of a right-angle triangle.
 2. Determine trigonometric ratios of a right-angle
triangle.
 3. Find the angle of a right-angle triangle using any of
trigonometric ratio.
LEARNING OUTCOME

4. PYTHAGORAS THEOREM
3 cm
4 cm
5 cm

5. PYTHAGORAS
THEORM
Use to measure
length of side
for a right-
angled triangle.
TRIGONOMETRIC
RATIOS
Use to measure
angle for a
right-angled
triangle.
PYTHAGORAS THEOREM
VS
TRIGONOMETRIC RATIOS

6. TRIGONOMETRIC RATIOS
3 cm
4 cm
5 cm
A

8. TRIGONOMETRIC RATIOS
3 cm
4 cm
5 cmB
sin 𝐵 =
4
5
cos 𝐵 =
3
5
tan 𝐵 =
4
3

9. B
B
B
B
B
B
B
B
B

10. 7 cm
24 cm
25 cm
𝜃
𝜃
𝜃

11. 𝜃
𝜃
𝜃
𝜃 𝜃
𝜃
𝜃
𝜃
𝜃
𝜃

12. ~LUCKY TRIG~
1 2 3
4 5 6

13. 5 m
12 m

14. 8 m
17 m
Q2: An ant climbs up 17 m from the bottom to the top of
the hill. The hill is 8 m height. Determine the value of ∡𝜃
using the diagram below.

15. 9 m
15 m
Q3: A boy wants to ski 15 m down a hill. The height of
the hill is 9 m. Determine the value of ∡𝜃 in the figure.

16. 9 cm
40 cm
41 cm

17. 11 cm
60 cm
61 cm

18. 12 cm
16 cm
20 cm

19.  Oh my sin 𝜃
 Goes opposite over hypotenuse
 Don’t forget my cos 𝜃
 The adjacent over hypotenuse
 Don’t get so confuse
 Of the tan 𝜃 I won’t loose
 Coz opposite over adjacent
 Is the thing I’ve learnt in lesson
TRIGO POEM