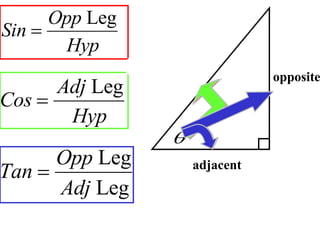
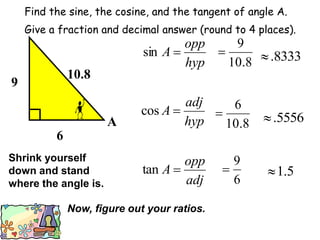
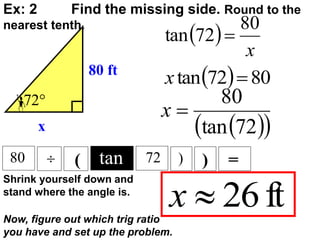
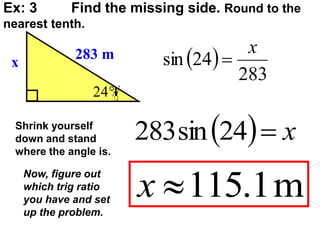
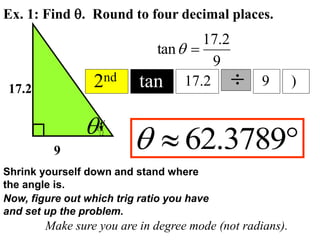
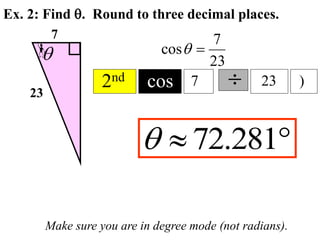
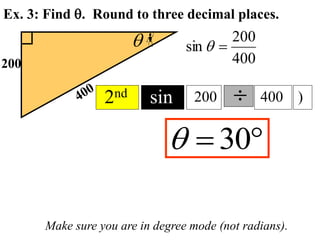
The document discusses trigonometric functions including sine, cosine, and tangent. It provides definitions and pronunciation for each term. It introduces SOHCAHTOA as a mnemonic device for remembering the definitions of sine, cosine, and tangent using opposite, adjacent, and hypotenuse ratios. Examples are given for finding trigonometric ratios, missing sides of triangles, and missing angles using appropriate trigonometric functions.

1. The Trigonometric Functions
we will be looking at
SINE
COSINE
TANGENT

2. The Trigonometric Functions
SINE
COSINE
TANGENT

3. SINE
Pronounced
“sign”

4. Pronounced
“co-sign”
COSINE

5. Pronounced
“tan-gent”
TANGENT

6. Prounounced
“theta”
Greek Letter q
Represents an unknown angle

7. q
opposite
hypotenuse
Sin
Opp
Hyp

Leg
adjacent
Cos
Adj
Hyp

Leg
Tan
Opp
Adj

Leg
Leg
hypotenuse
opposite
adjacent

8. We need a way to remember all of
these ratios…

9. Old Hippie
Some
Old
Hippie
Came
A
Hoppin’
Through
Our
Apartment

10. SOHCAHTOA
Old Hippie
Sin
Opp
Hyp
Cos
Adj
Hyp
Tan
Opp
Adj

11. Finding sin, cos, and
tan.
(Just writing a ratio or decimal.)

12. Find the sine, the cosine, and the tangent of angle A.
Give a fraction and decimal answer (round to 4 places).
hyp
opp
A 
sin
8
.
10
9
 8333
.

hyp
adj
A 
cos
8
.
10
6
 5556
.

adj
opp
A 
tan
6
9
 5
.
1

9
6
10.8
A
Shrink yourself
down and stand
where the angle is.
Now, figure out your ratios.

13. Find the sine, the cosine, and the tangent of angle A
A
24.5
23.1
8.2
hyp
opp
A 
sin
5
.
24
2
.
8
 3347
.

hyp
adj
A 
cos
5
.
24
1
.
23

9429
.

adj
opp
A 
tan
1
.
23
2
.
8
 3550
.

Give a fraction and
decimal answer (round
to 4 decimal places).
Shrink yourself
down and stand
where the angle is.
Now, figure out your ratios.

14. Finding a side.
(Figuring out which ratio to use and
getting to use a trig button.)

15. Ex: 1 Figure out which ratio to use. Find
x. Round to the nearest tenth.

55
20 m
x
 
20
55
tan
x

m
6
.
28

x
  x

55
tan
20
tan
20 55 )
Shrink yourself
down and stand
where the angle is.
Now, figure out
which trig ratio
you have and set
up the problem.

16. Ex: 2 Find the missing side. Round to the
nearest tenth.

72
80 ft
x
 
x
80
72
tan 
ft
26

x
  80
72
tan 
x
 
 
72
tan
80

x
tan
80 72 =
 ( ) )
Shrink yourself down and
stand where the angle is.
Now, figure out which trig ratio
you have and set up the problem.

17. Ex: 3 Find the missing side. Round to the
nearest tenth.

24
283 m
x  
283
24
sin
x

m
1
.
115

x
  x

24
sin
283
Shrink yourself
down and stand
where the angle is.
Now, figure out
which trig ratio
you have and set
up the problem.

18. Ex: 4 Find the missing side. Round to the
nearest tenth.

40
20 ft x  
20
40
cos
x

ft
3
.
15

x
  x

40
cos
20

19. Finding an angle.
(Figuring out which ratio to use and getting to use
the 2nd button and one of the trig buttons.)

20. Ex. 1: Find q. Round to four decimal places.
9
17.2
Make sure you are in degree mode (not radians).
9
2
.
17
tan 
q
q
2nd tan 17.2  9

 3789
.
62
q
)
Shrink yourself down and stand where
the angle is.
Now, figure out which trig ratio you have
and set up the problem.

21. Ex. 2: Find q. Round to three decimal places.
23
7
Make sure you are in degree mode (not radians).
23
7
cos 
q
q
2nd cos 7  23

 281
.
72
q
)

22. Ex. 3: Find q. Round to three decimal places.
200
Make sure you are in degree mode (not radians).
400
200
sin 
q
q
2nd sin 200  400

 30
q
)

23. When we are trying to find a side
we use sin, cos, or tan.
When we are trying to find an angle
we use sin-1, cos-1, or tan-1.