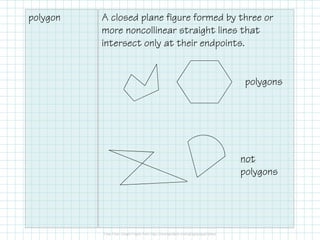
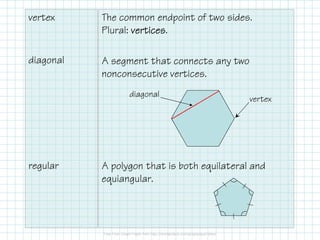
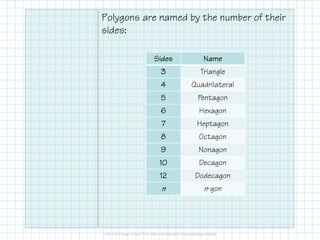
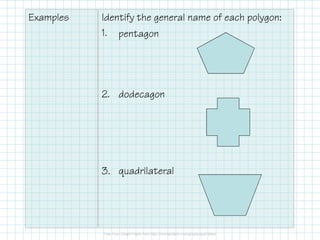
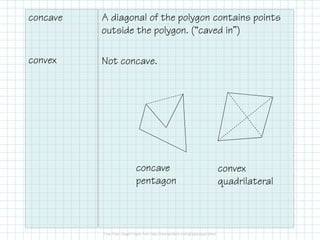
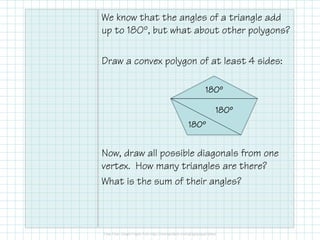
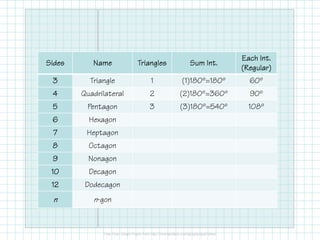
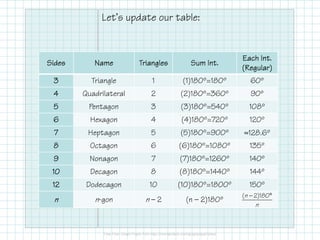
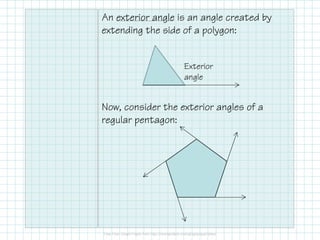
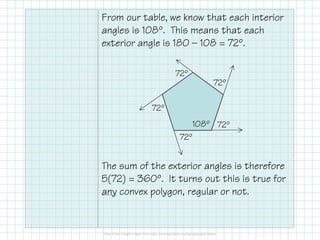
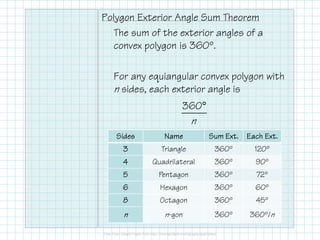
The document outlines key properties of polygons, including classification by sides, types (concave or convex), and angle relationships. It explains the polygon angle sum theorem and the calculation of interior and exterior angles for various polygon types. Additionally, it provides a table summarizing angle sums and measures for specific polygons.

1. Obj. 25 Properties of Polygons
The student is able to (I can):
• Name polygons based on their number of sides
• Classify polygons based on
— concave or convex
— equilateral, equiangular, regular
• Calculate and use the measures of interior and exterior
angles of polygons

2. polygon
A closed plane figure formed by three or
more noncollinear straight lines that
intersect only at their endpoints.
polygons
not
polygons

3. vertex
The common endpoint of two sides.
Plural: vertices
vertices.
diagonal
A segment that connects any two
nonconsecutive vertices.
diagonal
regular
vertex
A polygon that is both equilateral and
equiangular.

4. Polygons are named by the number of their
sides:
Sides
Name
3
Triangle
4
Quadrilateral
5
Pentagon
6
Hexagon
7
Heptagon
8
Octagon
9
Nonagon
10
Decagon
12
Dodecagon
n
n-gon

5. Examples
Identify the general name of each polygon:
1. pentagon
2. dodecagon
3. quadrilateral

6. concave
A diagonal of the polygon contains points
outside the polygon. (“caved in”)
convex
Not concave.
concave
pentagon
convex
quadrilateral

7. We know that the angles of a triangle add
up to 180º, but what about other polygons?
Draw a convex polygon of at least 4 sides:
180º
180º
180º
Now, draw all possible diagonals from one
vertex. How many triangles are there?
What is the sum of their angles?

8. Thm 6-1-1
Polygon Angle Sum Theorem
The sum of the interior angles of a
convex polygon with n sides is
(n — 2)180º
If the polygon is equiangular, then the
measure of one angle is
(n − 2)180°
n

9. Sides
Name
Triangles
Sum Int.
Each Int.
(Regular)
3
Triangle
1
(1)180º=180º
60º
4
Quadrilateral
2
(2)180º=360º
90º
5
Pentagon
3
(3)180º=540º
108º
6
Hexagon
7
Heptagon
8
Octagon
9
Nonagon
10
Decagon
12
Dodecagon
n
n-gon

10. Let’s update our table:
Sides
Name
Triangles
Sum Int.
Each Int.
(Regular)
3
Triangle
1
(1)180º=180º
60º
4
Quadrilateral
2
(2)180º=360º
90º
5
Pentagon
3
(3)180º=540º
108º
6
Hexagon
4
(4)180º=720º
120º
7
Heptagon
5
(5)180º=900º
≈128.6º
8
Octagon
6
(6)180º=1080º
135º
9
Nonagon
7
(7)180º=1260º
140º
10
Decagon
8
(8)180º=1440º
144º
12
Dodecagon
10
(10)180º=1800º
150º
n
n-gon
n—2
(n — 2)180º
(n − 2)180°
n

11. An exterior angle is an angle created by
extending the side of a polygon:
Exterior
angle
Now, consider the exterior angles of a
regular pentagon:

12. From our table, we know that each interior
angles is 108º. This means that each
exterior angle is 180 — 108 = 72º.
72º
72º
72º
108º 72º
72º
The sum of the exterior angles is therefore
5(72) = 360º. It turns out this is true for
any convex polygon, regular or not.

13. Polygon Exterior Angle Sum Theorem
The sum of the exterior angles of a
convex polygon is 360º.
For any equiangular convex polygon with
n sides, each exterior angle is
360°
n
Sides
Name
Sum Ext.
Each Ext.
3
Triangle
360º
120º
4
Quadrilateral
360º
90º
5
Pentagon
360º
72º
6
Hexagon
360º
60º
8
Octagon
360º
45º
n
n-gon
360º
360º/n