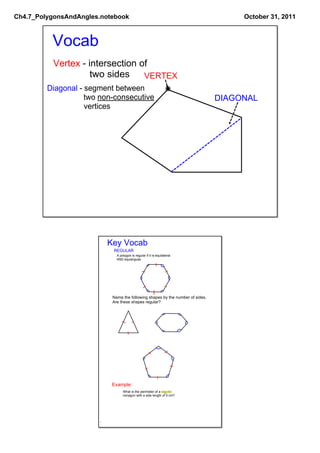
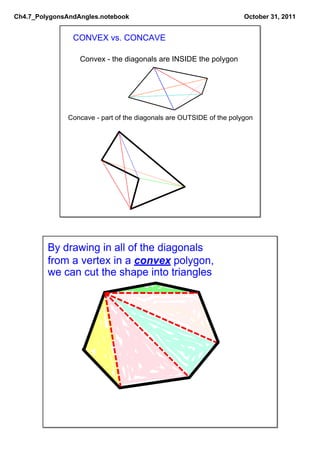
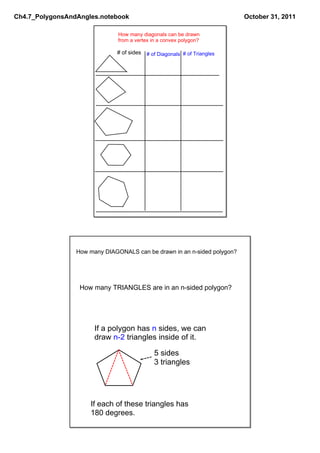
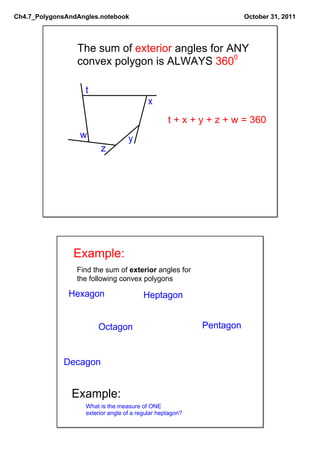
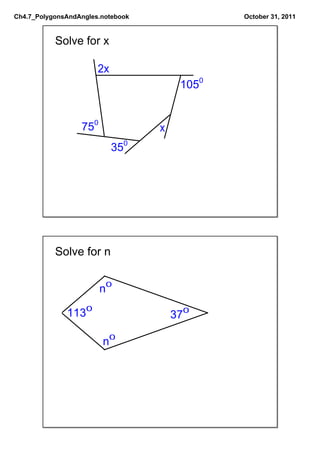
This document defines and discusses different types of polygons and angle measurements related to polygons. It introduces polygons based on the number of sides, such as triangles, quadrilaterals, pentagons, etc. It defines key terms like vertices and diagonals. It explains that regular polygons are equilateral and equiangular. It discusses the sums of interior and exterior angles for convex polygons and how to calculate the measurement of individual angles based on these sums and the number of sides.

1. Ch4.7_PolygonsAndAngles.notebook October 31, 2011
Chapter 4.7
Polygons and Angle Measure
Polygons are named for the number of sides
they have.
3 sides = triangle 8 sides = octagon
4 sides = quadrilateral 9 sides = nonagon
5 sides = pentagon 10 sides = decagon
6 sides = hexagon n sides = n-gon
7 sides = heptagon

2. Ch4.7_PolygonsAndAngles.notebook October 31, 2011
Vocab
Vertex ­ intersection of
two sides VERTEX
Diagonal ­ segment between
two non­consecutive DIAGONAL
vertices
Key Vocab
REGULAR
A polygon is regular if it is equilateral
AND equiangular
Name the following shapes by the number of sides.
Are these shapes regular?
Example:
What is the perimeter of a regular
nonagon with a side length of 5 cm?

3. Ch4.7_PolygonsAndAngles.notebook October 31, 2011
CONVEX vs. CONCAVE
Convex ­ the diagonals are INSIDE the polygon
Concave ­ part of the diagonals are OUTSIDE of the polygon
By drawing in all of the diagonals
from a vertex in a convex polygon,
we can cut the shape into triangles

4. Ch4.7_PolygonsAndAngles.notebook October 31, 2011
How many diagonals can be drawn
from a vertex in a convex polygon?
# of sides # of Diagonals # of Triangles
How many DIAGONALS can be drawn in an n­sided polygon?
How many TRIANGLES are in an n­sided polygon?
If a polygon has n sides, we can
draw n­2 triangles inside of it.
5 sides
3 triangles
If each of these triangles has
180 degrees.

5. Ch4.7_PolygonsAndAngles.notebook October 31, 2011
IMPORTANTE
If a convex polygon has n sides,
then the sum of interior angles is:
(n ­ 2) 180
Example: (n ­ 2) 180
Find the sum of interior angles for
the following convex polygons
Hexagon Heptagon
Octagon Pentagon
Decagon
Example
What is the measure of ONE
interior angle of a regular pentagon?
Sum of interior angles
(5 ­ 2) 180
3 180
5400
The measure of ONE angle is:
540 ÷ 5 = 1080
Example:
What is the measure of ONE
interior angle of a regular hexagon?

6. Ch4.7_PolygonsAndAngles.notebook October 31, 2011
The sum of exterior angles for ANY
convex polygon is ALWAYS 3600
t
x
t + x + y + z + w = 360
w y
z
Example:
Find the sum of exterior angles for
the following convex polygons
Hexagon Heptagon
Octagon Pentagon
Decagon
Example:
What is the measure of ONE
exterior angle of a regular heptagon?

7. Ch4.7_PolygonsAndAngles.notebook October 31, 2011
Solve for x
2x
1050
750 x
350
Solve for n
n0
1130 370
n0

8. Ch4.7_PolygonsAndAngles.notebook October 31, 2011
Formula Recap
Sum of Interior <'s Measure of ONE Interior <
(n­2) x 180 (n­2) x 180
n
Sum of Exterior <'s Measure of ONE Exterior <
3600 3600
n
Page 180:
#6­15, 19­21