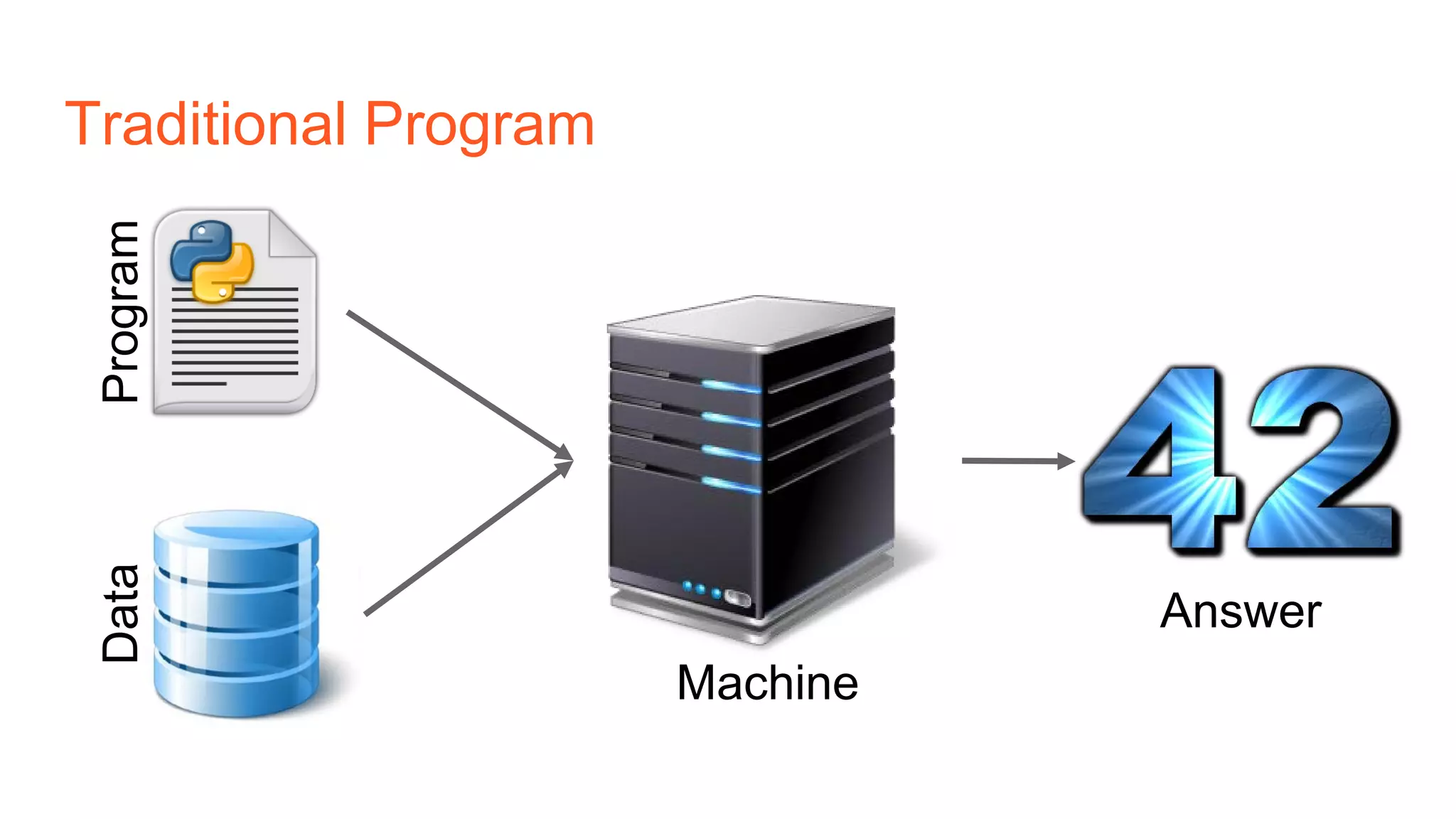
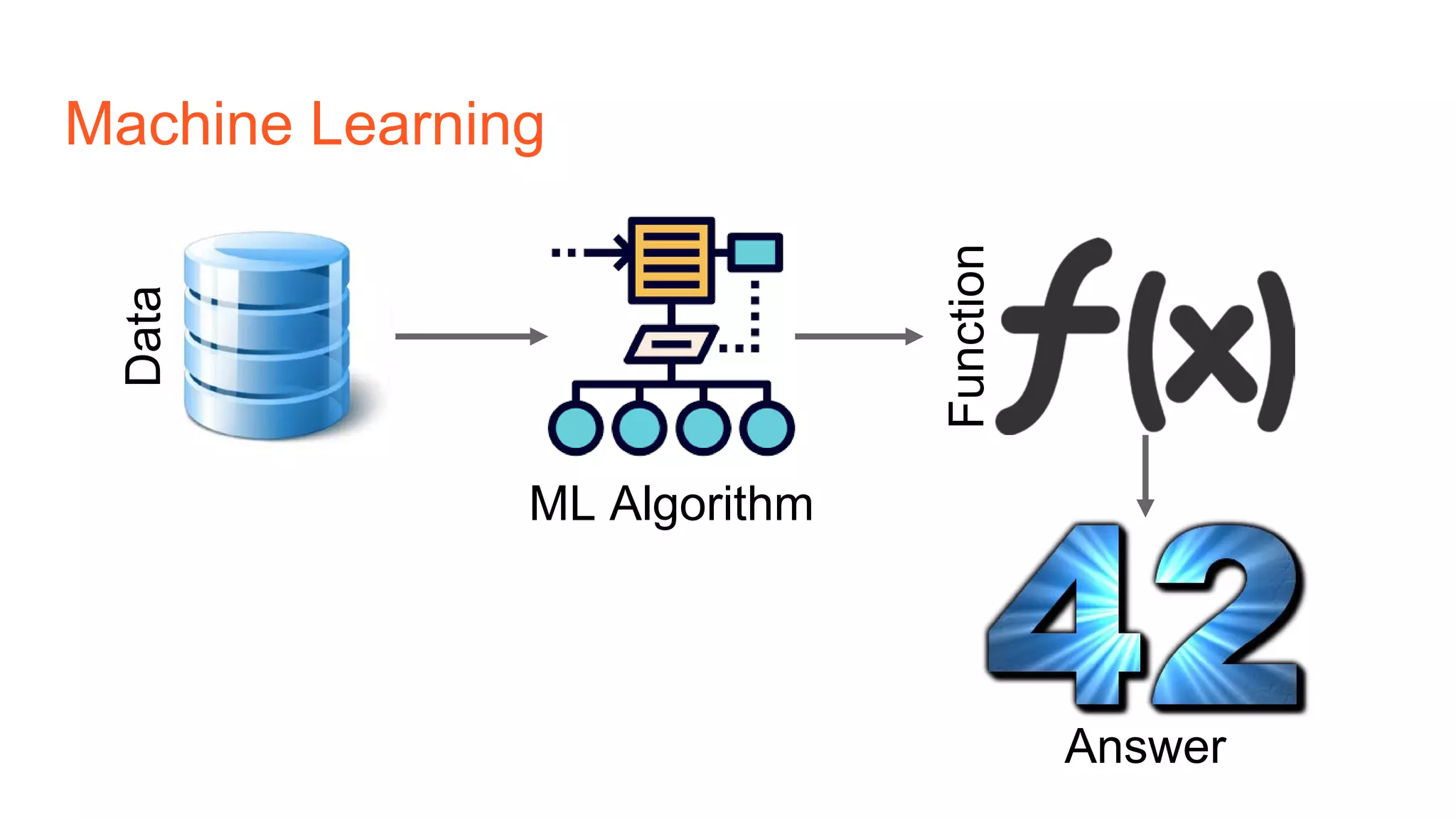
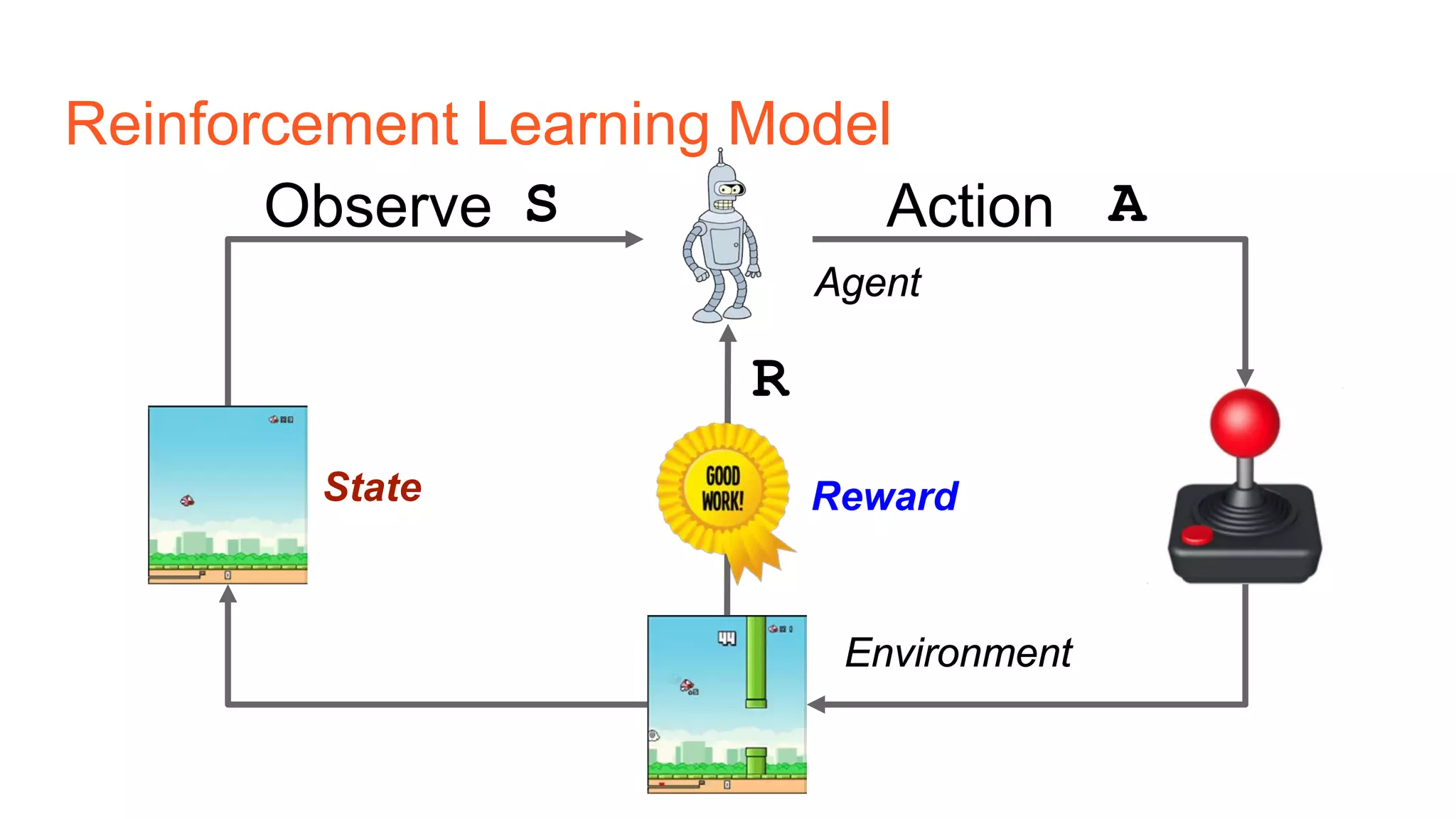
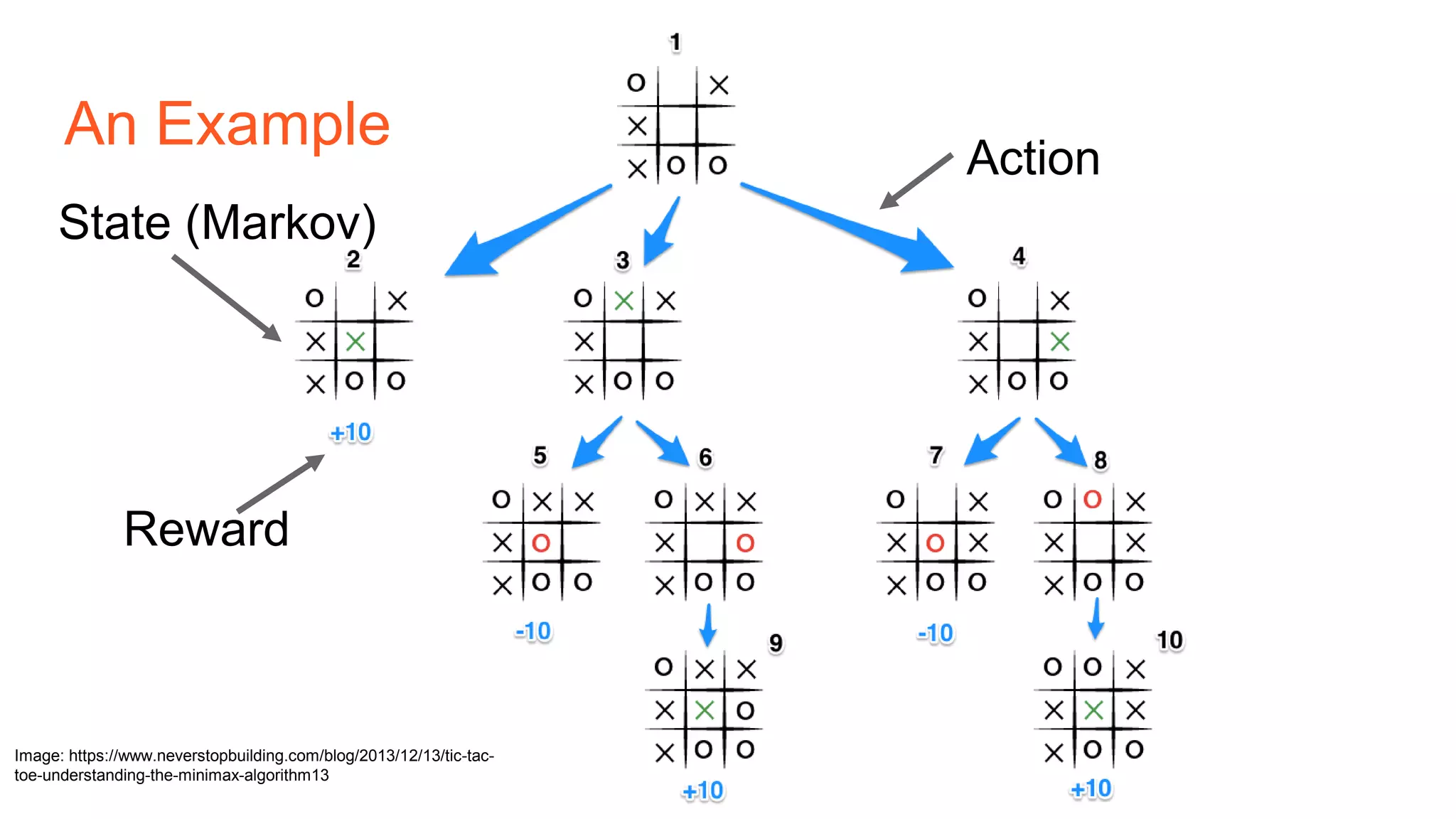
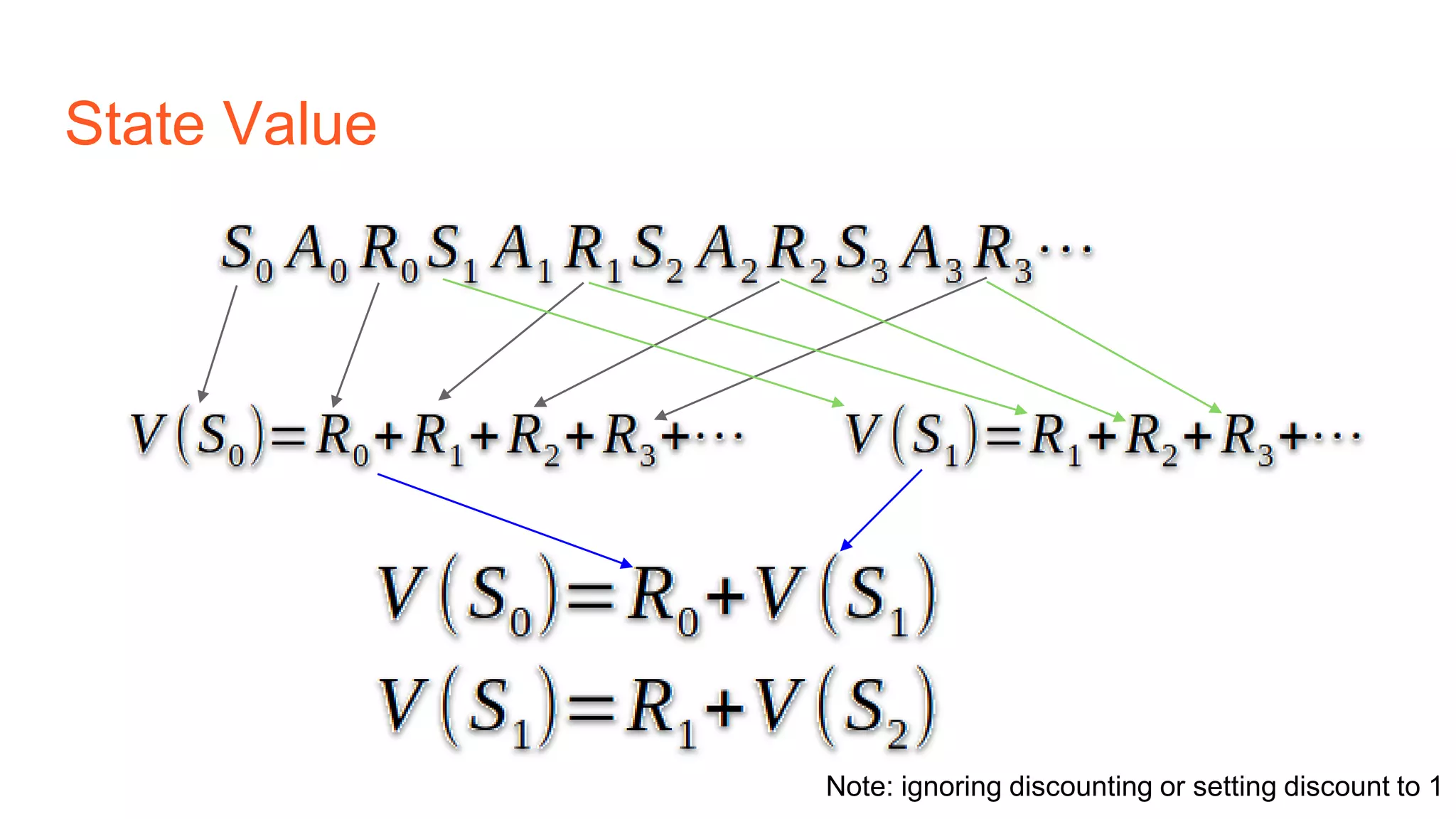
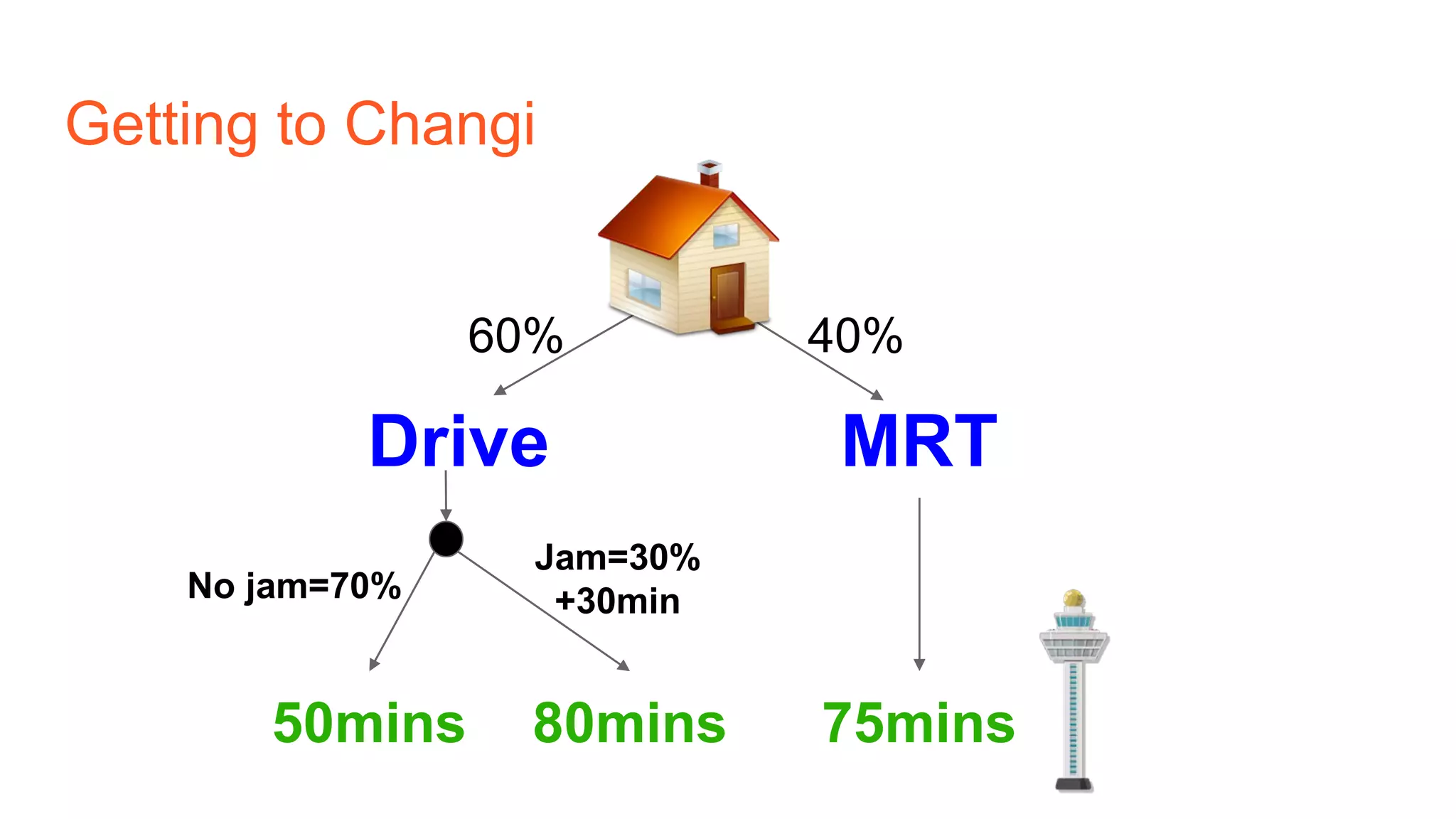
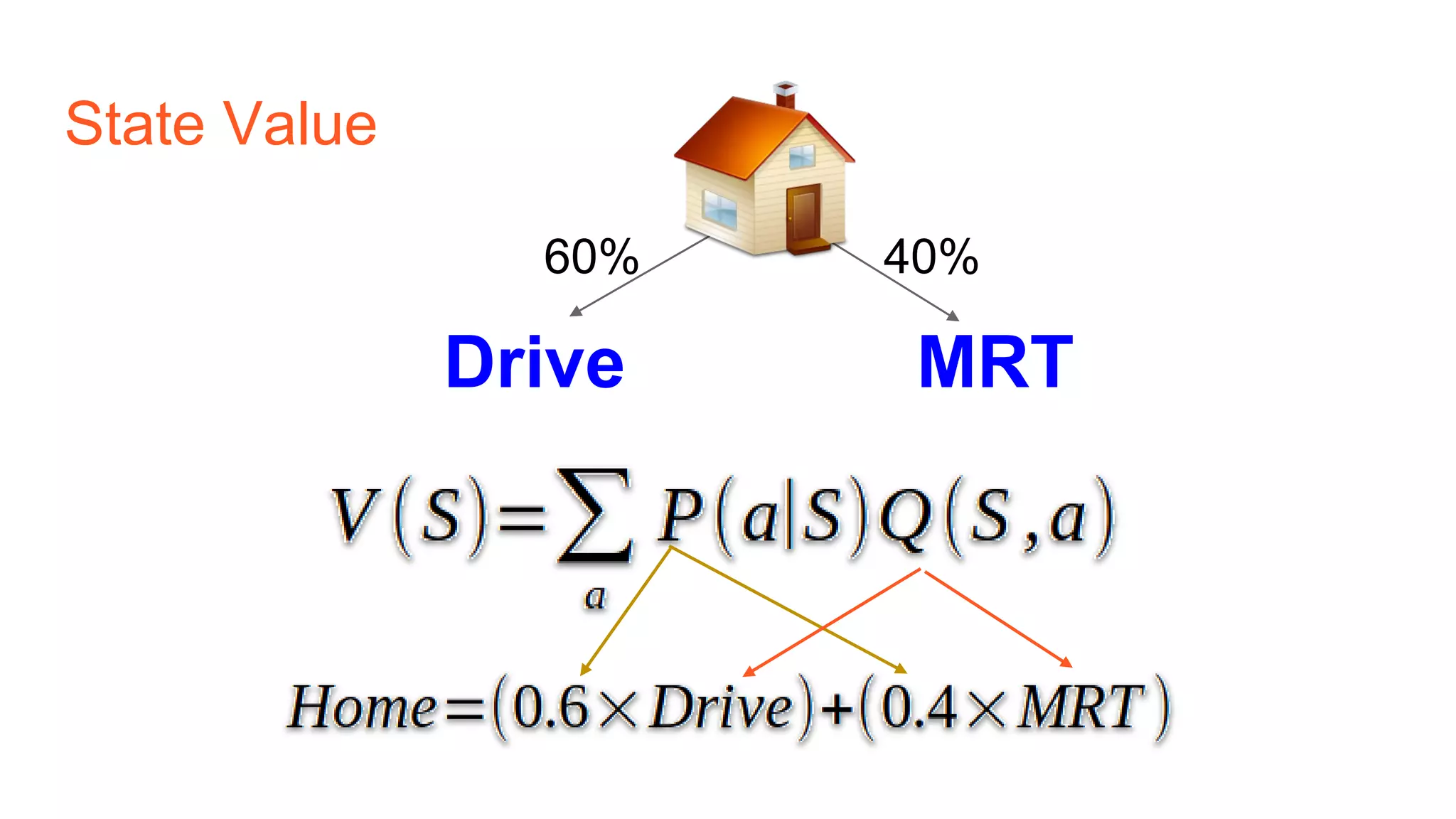
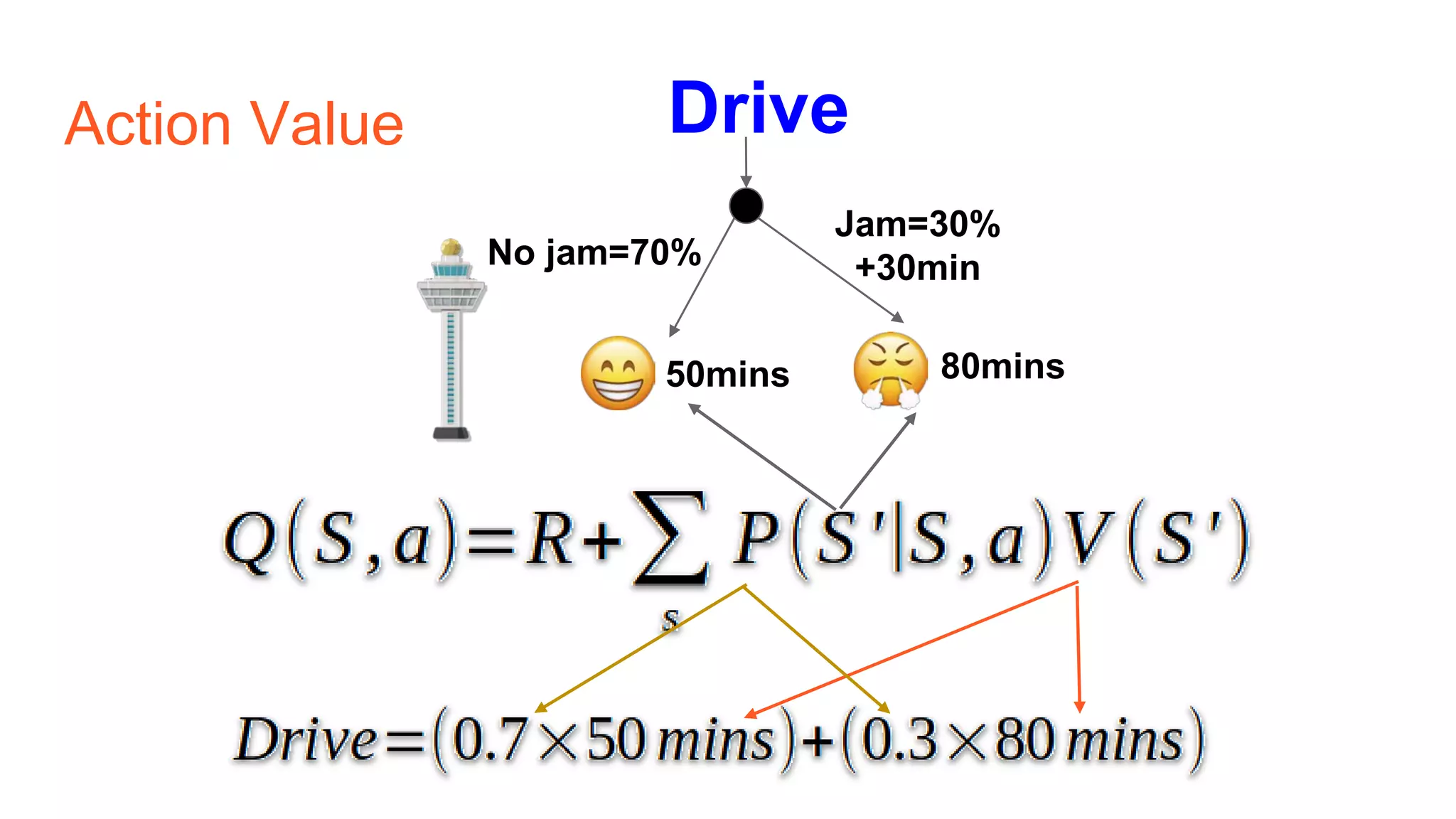
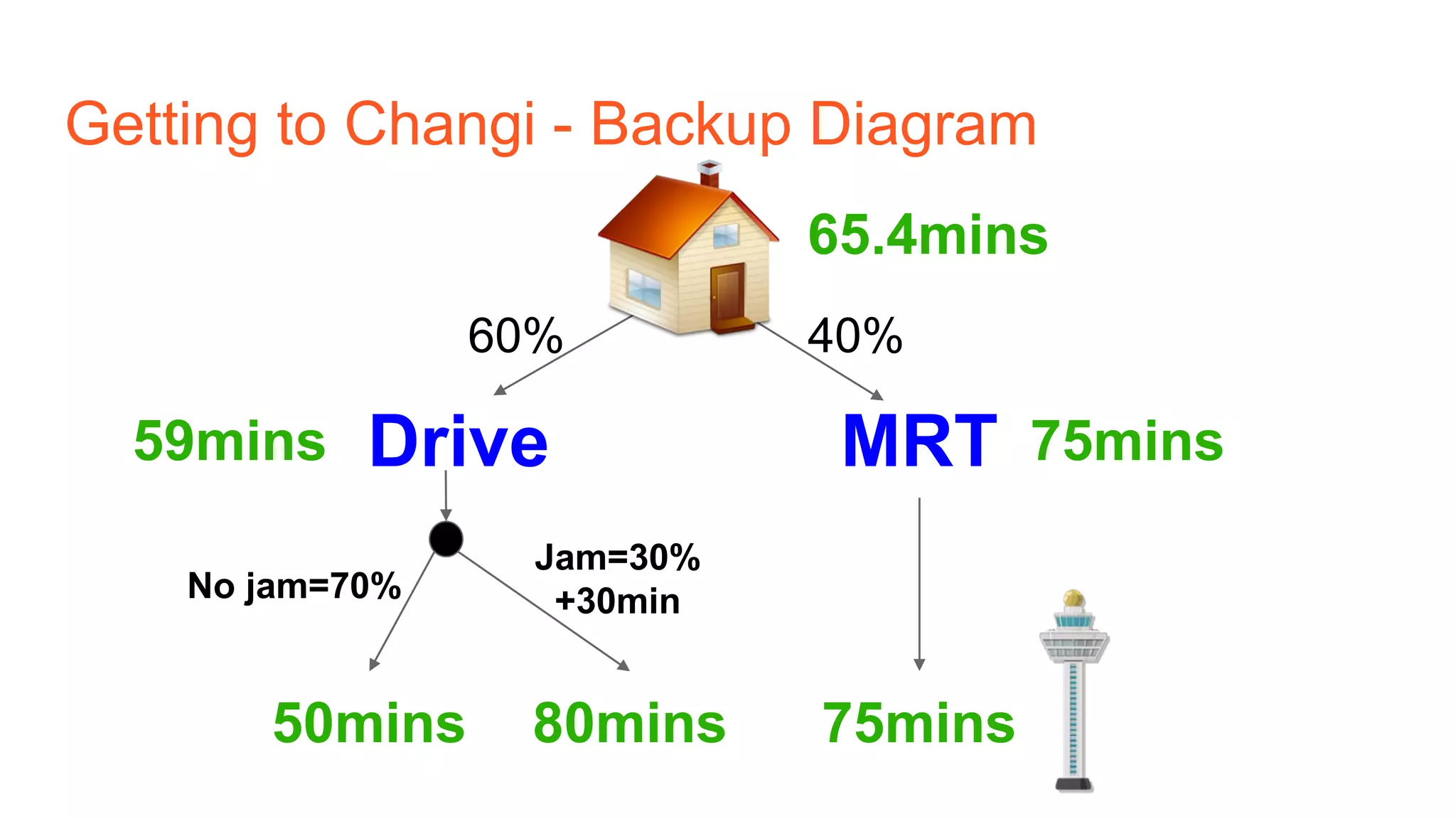
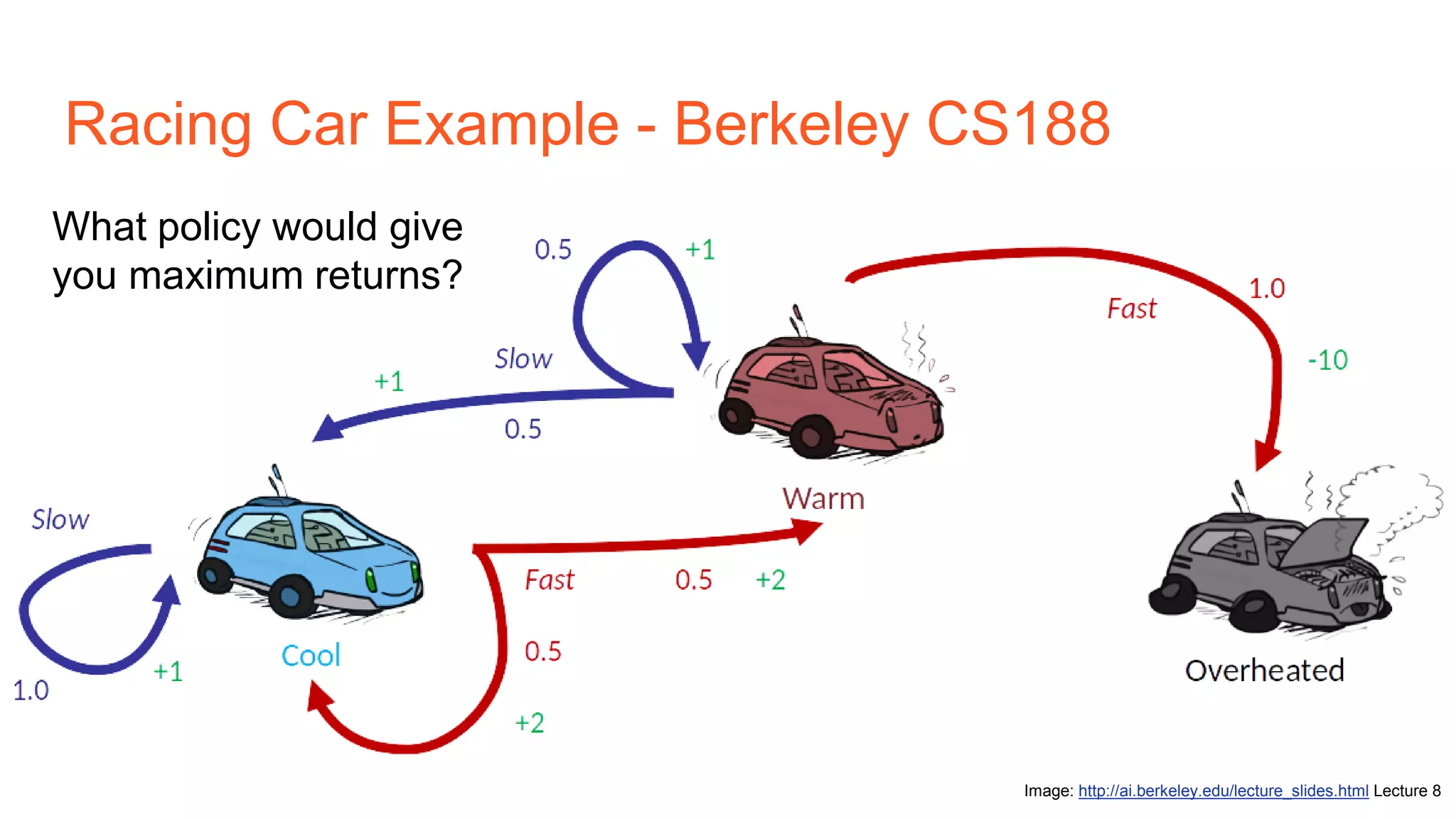
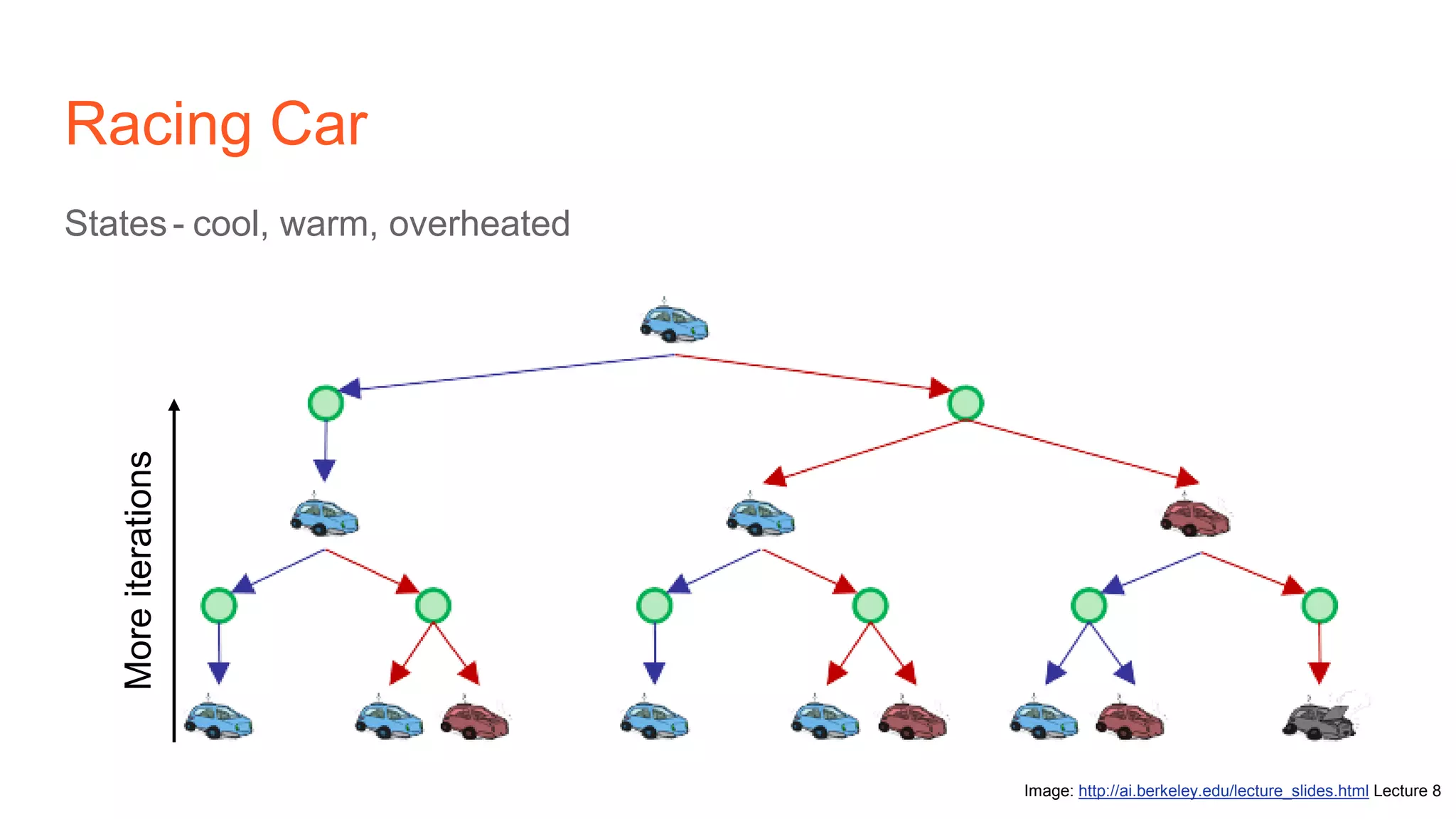
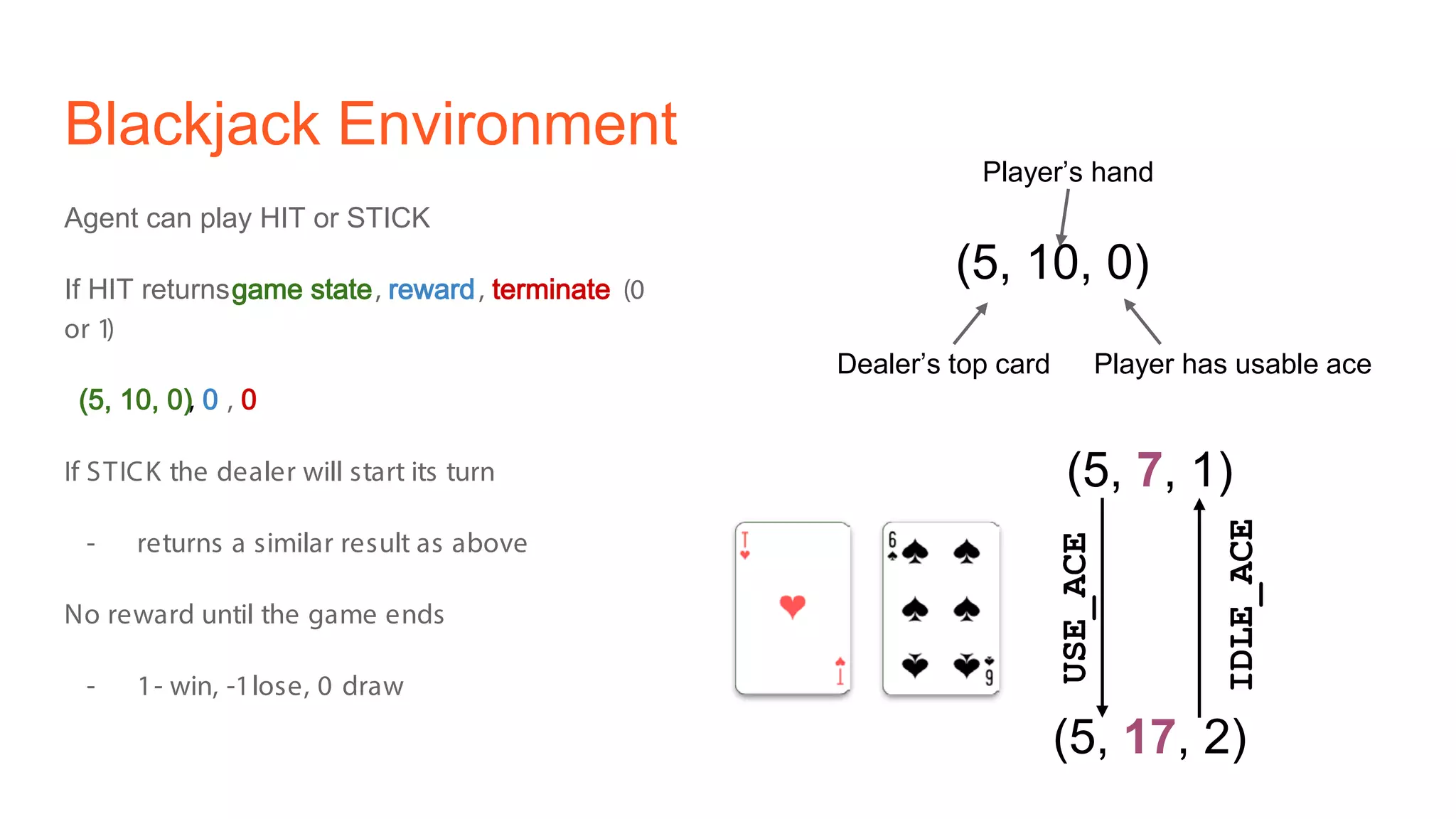
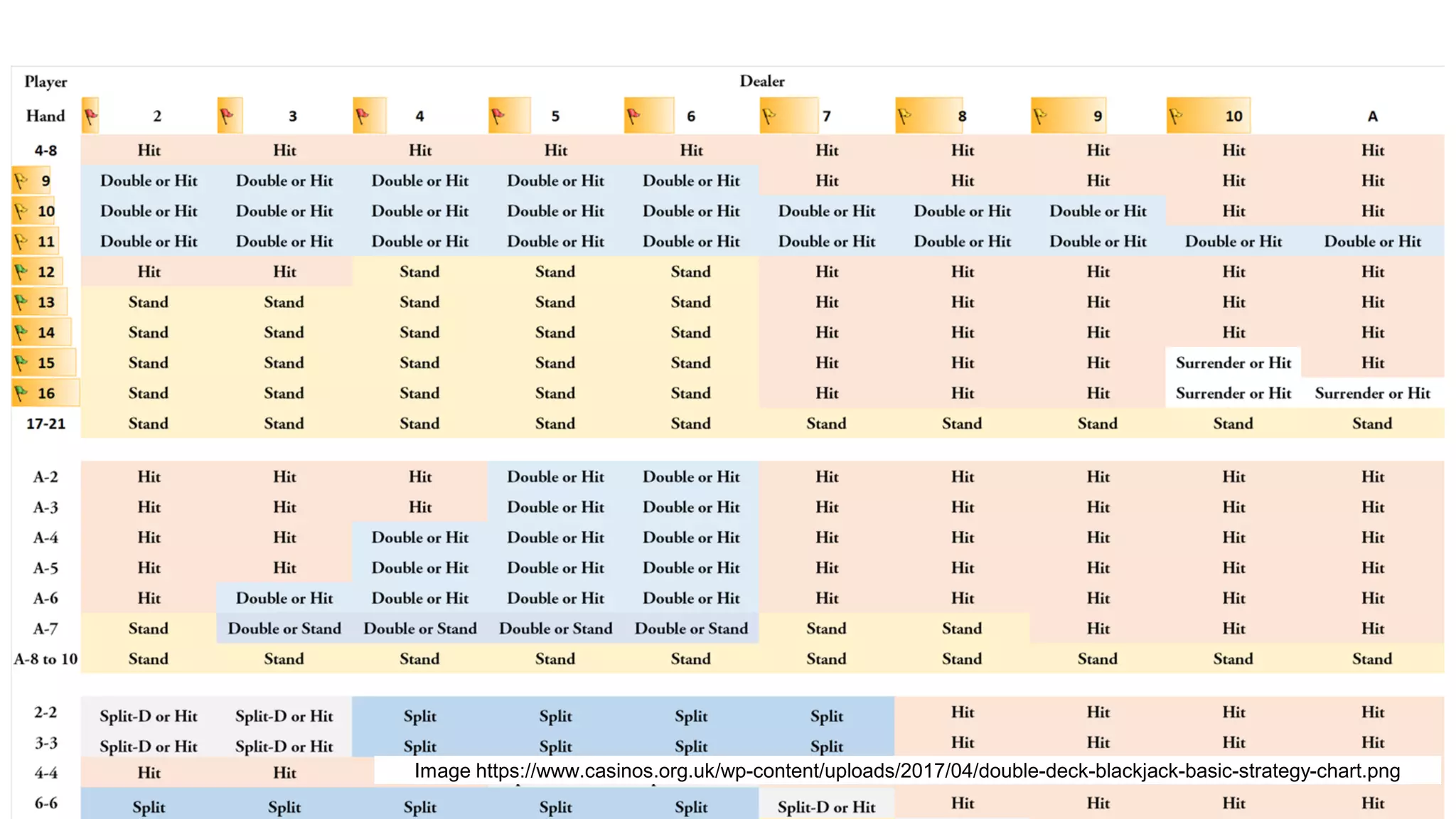
The document provides an introduction to reinforcement learning concepts like Markov decision processes, Monte Carlo methods, and epsilon-greedy policies and uses the example of training an agent to play the card game Blackjack using reinforcement learning. It describes the Blackjack environment and actions available to the agent as it learns through trial-and-error to develop a policy for maximizing its chances of winning games against a dealer.

1. How to train your agent to
play Blackjack
Lee Chuk Munn
chukmunnlee@nus.edu.sg
Slides athttps://bit.ly/agent2018

2. What is this talk about?
An introduction to key ideas in reinforcement learning
Conceptual, fairly high level
Intuition about the maths behind RL
Demos

3. What is Machine Learning?
“Machine learning is the field of
study that gives computers the
ability to learn without being
explicitly programmed”
Arthur Samuel

4. Programmed vs Learnt

5. Wrote the first
program that learn
how to play
checkers in 1959
Uses the minimax
algorithm
Arthur Samuel

6. Traditional ProgramProgramData
Machine
Answer

7. Machine LearningData
ML Algorithm
Function
Answer

8. How Do Machines Learn?
By generalizing - Supervised learning
- Give samples and answers to the sample
- Infer rules from the samples and the answer
By comparing - Unsupervised learning
- Give samples but do not give the answer
- Use some measurement to infer similarity by grouping them
By feedback - Reinforcement learning
- Do not give samples and answer
- Infer the rules from positive or negative feedback
Like babies

9. Reinforcement Learning
Learn by interacting with the environment
The experiences (rewards) will indicate if an action is good or bad
Image: https://medium.freecodecamp.org/an-introduction-
to-reinforcement-learning-4339519de419

10. ActionObserve
Agent
Environment
State Reward
Reinforcement Learning Model
S A
R

11. An Example
Image: https://www.neverstopbuilding.com/blog/2013/12/13/tic-tac-
toe-understanding-the-minimax-algorithm13
State (Markov)
Reward
Action

12. Trajectory
S0 Observe a
state
S0 A0 Take an action -
the policy
S0 A0 R0 Receive a reward -
feedback
S0 A0 R0 S1 Observe a new state
S0 A0 R0 S1 A1 Take another action

13. Policy and Cumulative Reward
Policy - how do you select the next
action?
Select the action so that will land you
on the best next state
How do you decide which is the best
next state?

14. State Value
Note: ignoring discounting or setting discount to 1

15. State Value
Estimate how good a state is with respect to how much cumulative reward I can get
from this point onwards
The better the returns the higher the state value
Some state values are real returns some are estimated

16. Action Value
What is the best action to take from a particular state
The best action is the action that will land me in the next best state
Actions that lead to states with high state values will have high action values

17. Getting to Changi
Drive MRT
60% 40%
Jam=30%
+30min
75mins50mins 80mins
No jam=70%

18. Getting to Changi
Estimated time to get from home to airport is ≅65mins

19. State Value
Drive MRT
60% 40%

20. Action Value Drive
Jam=30%
+30minNo jam=70%
50mins 80mins

21. Getting to Changi - Backup Diagram
Drive MRT
60% 40%
Jam=30%
+30min
75mins50mins 80mins
No jam=70%
59mins 75mins
65.4mins

22. Racing Car Example - Berkeley CS188
Image: http://ai.berkeley.edu/lecture_slides.html Lecture 8
What policy would give
you maximum returns?

23. Racing Car
States- cool, warm, overheated
Image: http://ai.berkeley.edu/lecture_slides.html Lecture 8
Moreiterations

24. Calculate the State Value
Recursive definition. The
equation bootstrap off
each other
Image: http://ai.berkeley.edu/lecture_slides.html Lecture 8

25. State Values for 5 Iterations
State values
cool warm
overheated
V0 0 0 0
V1 3.0 -9.0 0
V2 3.0 -12.0 0
V3 1.5 -13.5 0
V4 -1.5 -15.0 0
V5 -6.75 -17.25 0
How good is it to be in a state? Why are the state
values so bad?

26. Action Value
No way to make decision with state value
For every state find the best action
Treat this as an array of terms. max
behaves like Python max() function

27. Action Value for 3 Iterations
S0 action {'cool': 0, 'warm': 0, 'overheated': 0}
S1 action {'cool': 2.0, 'warm': 1.0}
{'cool': 'fast', 'warm': 'slow'}
S2 action {'cool': 3.5, 'warm': 2.5}
{'cool': 'fast', 'warm': 'slow'}
S3 action {'cool': 5.0, 'warm': 4.0}
{'cool': 'fast', 'warm': 'slow'}
S4 action {'cool': 6.5, 'warm': 5.5}
{'cool': 'fast', 'warm': 'slow'}

28. What if you don’t have the model?
Laws of
Large Numbers

29. Model Free
Model free - no knowledge of MDP viz. the transitions probability and reward
Approximate the probability of certain outcomes by running multiple trials
Monte Carlo methods learn directly from episodes of experiences
F +2 F -10
F +2 F +1 F +2 F -10

30. Monte Carlo Algorithm
Generate an episode using your current agent’s policy
(c, f, +2, w), (w, f, 1, c), (c, f, +2, w), (w, f, -10, o)
Average the return for the first occurrence of (state, action) pair
(c, f) = 2 + 1 + 2 + -10 / 1 = -5
(w, f) = 1 + 2 + -10 / 1 = -7
Use the slightly new policy to generate another episode
F +2 F +1 F +2 F -10
Policy emerging.
“Going fast in cold state is
better than going fast in
warm state”

31. Monte Carlo Algorithm
Laws of large numbers only works if you havelots of varied data
Require to explore all possible (state, action) pair
Current policy is ‘greedy’ - only select the best action for a state
Not an issue if its model-based

32. Explore vs Exploit
Greedy policy will always eat the berger
ε-greedy policy will try the salad once in a blue moon

33. ε-Greedy Policy
With a probability ε select a random action
Decay ε over time
- Want the policy to be more exploratory in the beginning and more exploitive
later as the policy converges

34. Blackjack Rules
Objective is to get as close as possible to 21 without going over
Each player deals 2 cards
Natural - ‘ten-card’ and Ace
Usable Ace - An Ace can be considered as 1 or 11
Draw cards - HIT, Stop drawing cards- STICK
Player draws card. When STICK, then dealer’s turn to HIT
Player hand must be 15 before STICKING, Dealer 17 before STICKING

35. Blackjack Environment
Agent can play HIT or STICK
If HIT returnsgame state, reward, terminate (0
or 1)
(5, 10, 0), 0 , 0
If STICK the dealer will start its turn
- returns a similar result as above
No reward until the game ends
- 1- win, -1lose, 0 draw
(5, 10, 0)
Dealer’s top card
Player’s hand
Player has usable ace
(5, 7, 1)
(5, 17, 2)
USE_ACE
IDLE_ACE

36. Blackjack Agent
Only knows the following actions: HIT, STICK, USE_ACE, IDLE_ACE
- Does not know what the action does
Have to learn the following
- Blackjack rules
- Policy to maximize the chances of winning
Lose, reward ==-1, if
- play USE_ACE when there is no ACE
- play IDLE_ACE when there is no ACE or have not played USE_ACE
- STICK if the hand is less than 15
- Bust if hand is greater than 21

37. Demo

38. Image https://www.casinos.org.uk/wp-content/uploads/2017/04/double-deck-blackjack-basic-strategy-chart.png

39. Where can I learn more?
Berkeley CS188- http://ai.berkeley.edu/lecture_slides.html (MDP)
David Silver- http://www0.cs.ucl.ac.uk/staff/D.Silver/web/Teaching.html
Reinforcement Learning - An Introduction
by Richard S Sutton and Andrew G Barto
http://www.incompleteideas.net/book/bookdraft2017no
v5.pdf