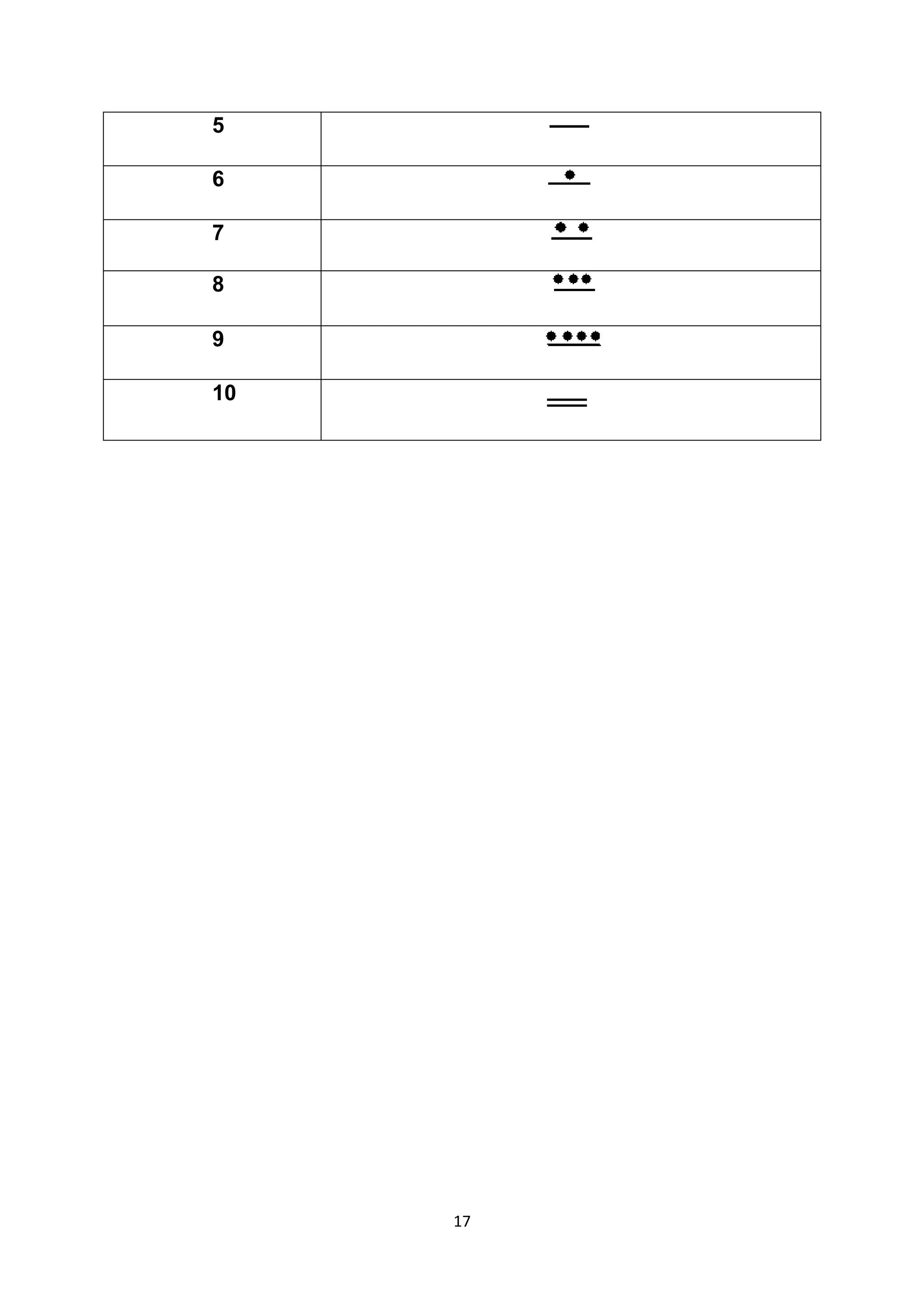
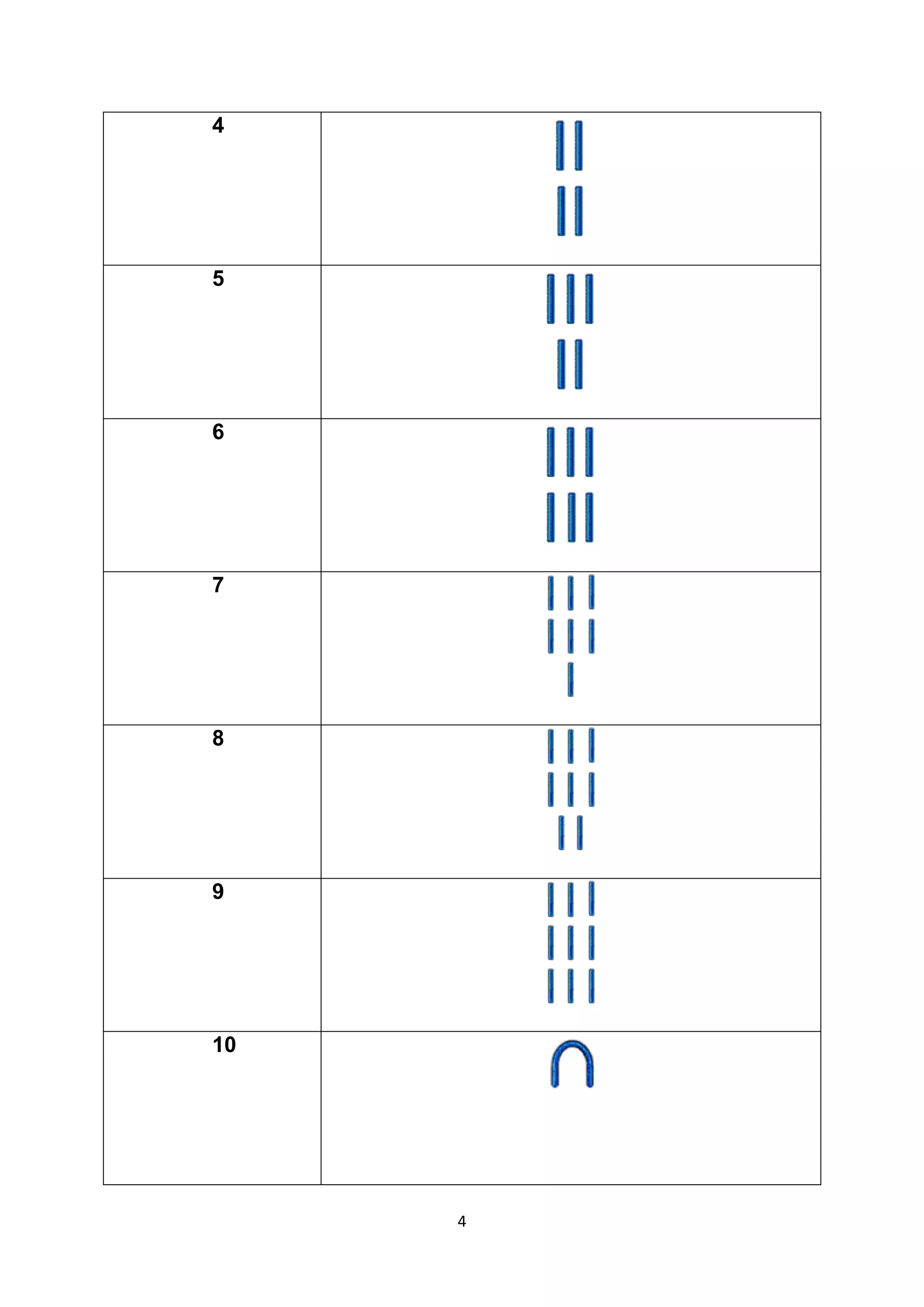
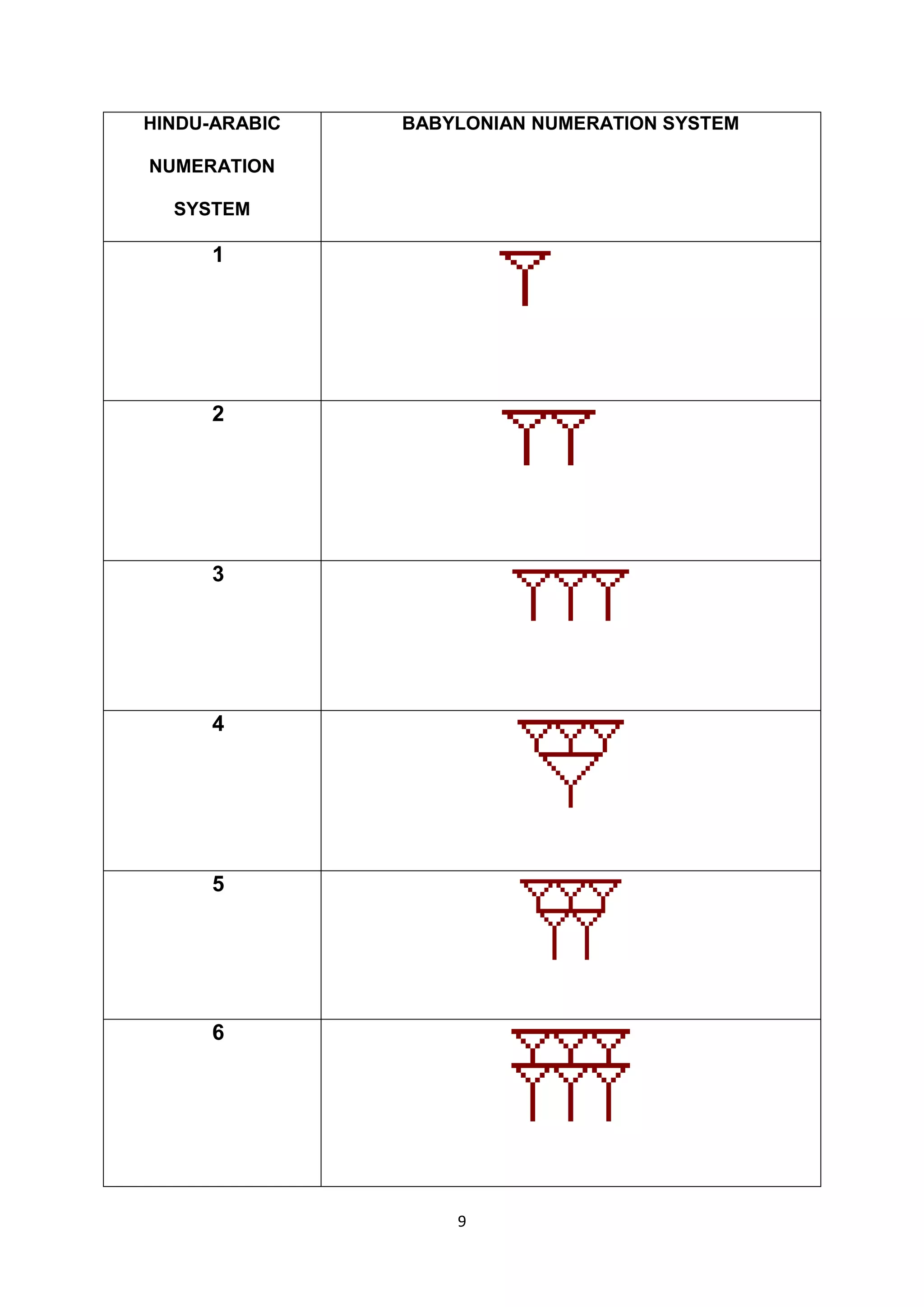
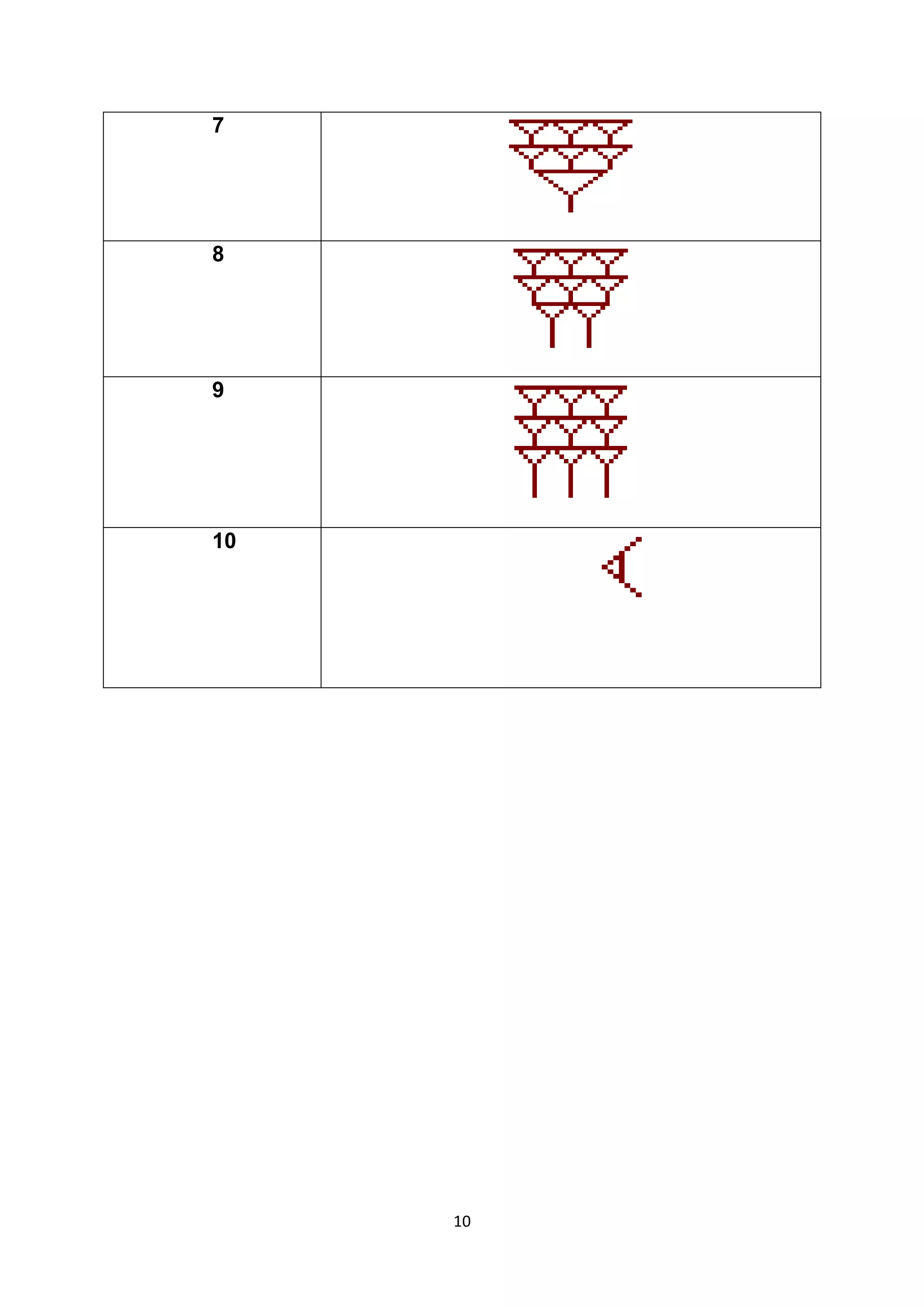
The document discusses several ancient numeration systems including the Egyptian, Babylonian, Roman, Mayan, and Hindu-Arabic systems. It provides examples of how each system represented numbers from 1 to 10. The Egyptian system used pictographs for the first nine numbers and logographs for higher numbers. The Babylonian system used a base-60 place value system with symbols for 1 and 10, requiring context to distinguish numbers. The Roman system used additive and subtractive principles with symbols for 1, 5, 10, 50, 100, 500, and 1000. The Mayan system was a base-20 place value system using dots, bars, and shells to represent numbers up to 19.

1. 2.0 THE FIRST TEN NUMBERS OF EACH
NUMERATION SYSTEM
2.1 EGYPTIAN NUMERATION SYSTEM
One of the earliest examples of a numeral system is the Egyptian
numeral system, based on the following hieroglyphs:
If we look at the diagram above, we will notice that the first nine
numerals are pictographic in character, but the remaining ones are
logographic in character. Notice also that this is a decimal system.
However, it does not tell us how the Egyptians wrote compound
numerals. As it turns out, the Egyptians used a simple additive system,
as illustrated in the following diagrams.
2

2. Note carefully that although the Egyptian numeral system does
not especially require a symbol for zero, the Egyptians nevertheless
had a symbol for zero
which they used for a variety of engineering and accounting purposes,
including some rather astonishing projects, such as the Pyramids
which were constructed during 2550 BC.
HINDU-ARABIC EGYPTIAN NUMERATION SYSTEM
NUMERATION
SYSTEM
1
2
3
3

3. 4
5
6
7
8
9
10
4

4. 2.2 BABYLONIAN NUMERATION SYSTEM
The Babylonians lived in Mesopotamia, which is between the Tigris
and Euphrates rivers. They began a numbering system about 5,000
years ago. It is one of the oldest numbering systems.
The first mathematics can be traced to the ancient country of
Babylon, during the third millennium B.C. Tables were the Babylonians
most outstanding accomplishment which helped them in calculating
problems. The Babylonian numeration system was developed between
3000 and 2000 BCE.
It uses only two numerals or symbols, a one and a ten to represent
numbers and they looked these:
To represent numbers from 2 to 59, the system was simply additives.
The Babylonian number system began with tally marks just as most of
the ancient math systems did. The Babylonians developed a form of
writing based on cuneiform. Cuneiform means "wedge shape" in Latin.
They wrote these symbols on wet clay tablets which were baked in the
hot sun. Many thousands of these tablets are still around today. The
Babylonians used a stylist to imprint the symbols on the clay since
curved lines could not be drawn.
The Babylonians had a very advanced number system even for
today's standards. It was a base 60 system (sexagesimals) rather than
a base ten (decimal). Base ten is what we use today.
5

5. The Babylonians divided the day into twenty-four hours, each
hour into sixty minutes, and each minute to sixty seconds. This form of
counting has survived for four thousand years.
Example#1:
5 is written as shown:
12 are written as shown:
Notice how the ones, in this case two ones are shown on the right just
like the Hindu-Arabic numeration system
45 is written as shown:
For number bigger than 59, the Babylonian used a place value system
with a base of 60
6

6. 62 is written as shown:
Notice this time the use of a big space to separate the space value
Without the big space, things look like this:
However, what is that number without this big space? Could it be 2 ×
60 + 1 or 1× 602 + 1 × 60 + 1 or???
The Babylonians introduced the big space after they became aware of
this ambiguity.
The number 4871 could be represented as follow: 3600 + 1260 + 11 =
4871
7

7. Even after the big space was introduced to separate place value, the
Babylonians still faced a more serious problem?
Since there was no zero to put in an empty position, the number 60
would thus have the same representation as the number 1
How did they make the difference? All we can say is that the context
must have helped them to establish such difference yet the Babylonian
numeration system was without a doubt a very ambiguous numeral
system.
If this had become a major problem, no doubt the Babylonians were
smart enough to come up with a working system.
8

8. HINDU-ARABIC BABYLONIAN NUMERATION SYSTEM
NUMERATION
SYSTEM
1
2
3
4
5
6
9

9. 7
8
9
10
10

10. 2.3 ROMAN NUMERATION SYSTEM
Before Rome, the most developed civilization on the Italic Peninsula
was the Etruscan civilization, who copied their numerals from the early
Greek (Attic) system. These numerals were adopted and adapted by
the Romans, who formulated the Roman numeral system, still in wide
use today for a variety of purposes. There are other Roman numerals
that most of us never learn, but can be found in Latin dictionaries – for
example:
5000 I>>
10000 ==I>>
50000 I>>>
100000 ===I>>>
500000 I>>>>
1000000 ====I>>>>
As every grade school child knows, the Roman numeral system
is based on the following seven atomic numerals:
IVXLCDM
1 5 10 50 100 500 1000
The Roman numeral system is not a simple additive system, but
is rather an additive-subtractive system. In fact, the subtractive aspect
is frequently a source of worry when reading large numerals – for
example:
MCMXCIX
By saying that the Roman system is (partly) subtractive, we
mean that some combinations of symbols require us to apply
subtraction in order to interpret them. For example, IV stands for “one
before five”, which is four [i.e., 5 minus 1]. Similarly, the numeral XC
11

11. stands for “ten before one-hundred”, which is ninety [i.e., 100 minus
10]. On the other hand, the string IC is officially ill-formed, although it
could be understood to mean “one before one-hundred”, which would
then be ninety-nine. So how do we interpret a Roman numeral such as
„MCMXCIX‟?
M is not before a larger numeral, so it reads: + 1000 1000
C is before a larger numeral, so it reads: - 100
M is after a negative prefix, so it reads: + 1000 900
X is before a larger numeral, so it reads: - 10
C is after a negative prefix, so it reads: + 100 90
I is before a larger numeral, so it reads: - 1
X is after a negative prefix, so it reads: + 10 9
Thus, „MCMXCIX‟ represents the number 1999.
HINDU-ARABIC ROMAN NUMERATION SYSTEM
NUMERATION
SYSTEM
1 I
2 II
3 III
4 IV
5 V
6 VI
7 VII
8 VIII
9 IX
12

12. 10 X
2.4 MAYAN NUMERATION SYSTEM
The Mayan number system dates back to the fourth century and was
approximately 1,000 years more advanced than the Europeans of that time.
This system is unique to our current decimal system, which has a base 10, in
that the Mayan's used a base 20.
This system is believed to have been used because, since the Mayan's
lived in such a warm climate and there was rarely a need to wear shoes, 20
was the total number of fingers and toes, thus making the system workable.
Therefore two important markers in this system are 20, which relates to the
fingers and toes, and five, which relates to the number of digits on one hand
or foot. The Mayan numeration system evolved around A.D. 300. It uses 3
basic numerals to represent any possible number: a dot for one, a horizontal
bar for 5, and a conch shell for zero.
The Mayan's were also the first to symbolize the concept of nothing (or
zero). The most common symbol was that of a shell ( ) but there were several
other symbols (e.g. a head). It is interesting to learn that with all of the great
mathematicians and scientists that were around in ancient Greece and Rome,
it was the Mayan Indians who independently came up with this symbol which
usually meant completion as opposed to zero or nothing.
They used the 3 symbols above to represent the numbers from 0
through 19 as shown below:
13

13. For number bigger than 19, a number is written in a vertical position so
that it becomes a vertical place value system. Initially, the base used in the
Mayan numeration system was base 20 and their place values were 1, 20,
202, 203,
Then, they changed their place values to 1, 20, 20 × 18, 20 2 × 18, 203× 18, ...
Using the base 20, 1, 20, 202,203, ..., we can write 20 as follow:
In the ones place we have 0 and in the twenties place we have 1, so
the number is
0 × 1 + 1 × 20 = 0 + 20 = 20
Still using a base of 20, we can write 100 as follow:
0 × 1 + 5 × 20 = 0 + 20 = 100
Below is how to represent 2007
14

14. 5 × 202 + 0 × 20 + 7 = 5 × 400 + 0 + 7 = 2000 + 7 = 2007
It is started from the bottom, a place value must have a number from the list
above.
(1-19)
Look carefully and see how it was separated into the place values.
Again, it was separated according to numbers that are the list above from 1
through 19
The number is: 14 + 7 × 20 + 1 × 202 + 3 × 20 3 + 0 × 20 4 + 15 × 20 5 + 5 ×
20 6
The number is 14 + 140 + 1 × 400 + 3 × 8,000 + 0 + 15 × 3,200,000 + 5×
64,000,000
The number is = 14 + 140 + 400 + 24,000 + 0 + 48,000,000 + 320,000,000 =
15

15. 368024554
With the base 1, 20, 20 × 18, 202 × 18, 203× 18, ... computation is done the
exact same way!
Group as shown below:
The number is 11 × 1 + 1 × 20 + 10 × 20 × 18 = 11 + 20 + 3600 = 3631
No doubt; the Mayan numeration system was sophisticated.
HINDU-ARABIC MAYAN NUMERATION SYSTEM
NUMERATION
SYSTEM
1
2
3
4
16

16. 5
6
7
8
9
10
17

17. 2.5 WORD PROBLEM AND ITS SOLUTION
Question:
One of the natives on the island named Karu. One day, he went out to
find food. He collected 41 carrots, 26 clams, 13 fishes and a dozen
bananas in a big rattan basket. He felt hungry so he decided to eat 3
carrots and 5 fishes. As he was about to go back home, he fell onto
the ground and lost 20 clams and 24 carrots. On seeing Karu was
injured, a monkey quickly stole 3 bananas. How many carrots, clams,
fishes and bananas left in the rattan basket at last?
Answer:
Carrots:
41- 3 – 24 = 14
Clams:
26 – 20 = 6
Fishes:
13 – 5 = 8
Bananas:
12 – 3 = 9
18

18. TRANSLATION INTO BABYLONIAN WRITING
:
.
.
19

19. ,
,
.
20

20. .
,
.
,
21

21. .
,
,
?
22

22. :
:
- - =
:
- =
:
- =
:
- =
23