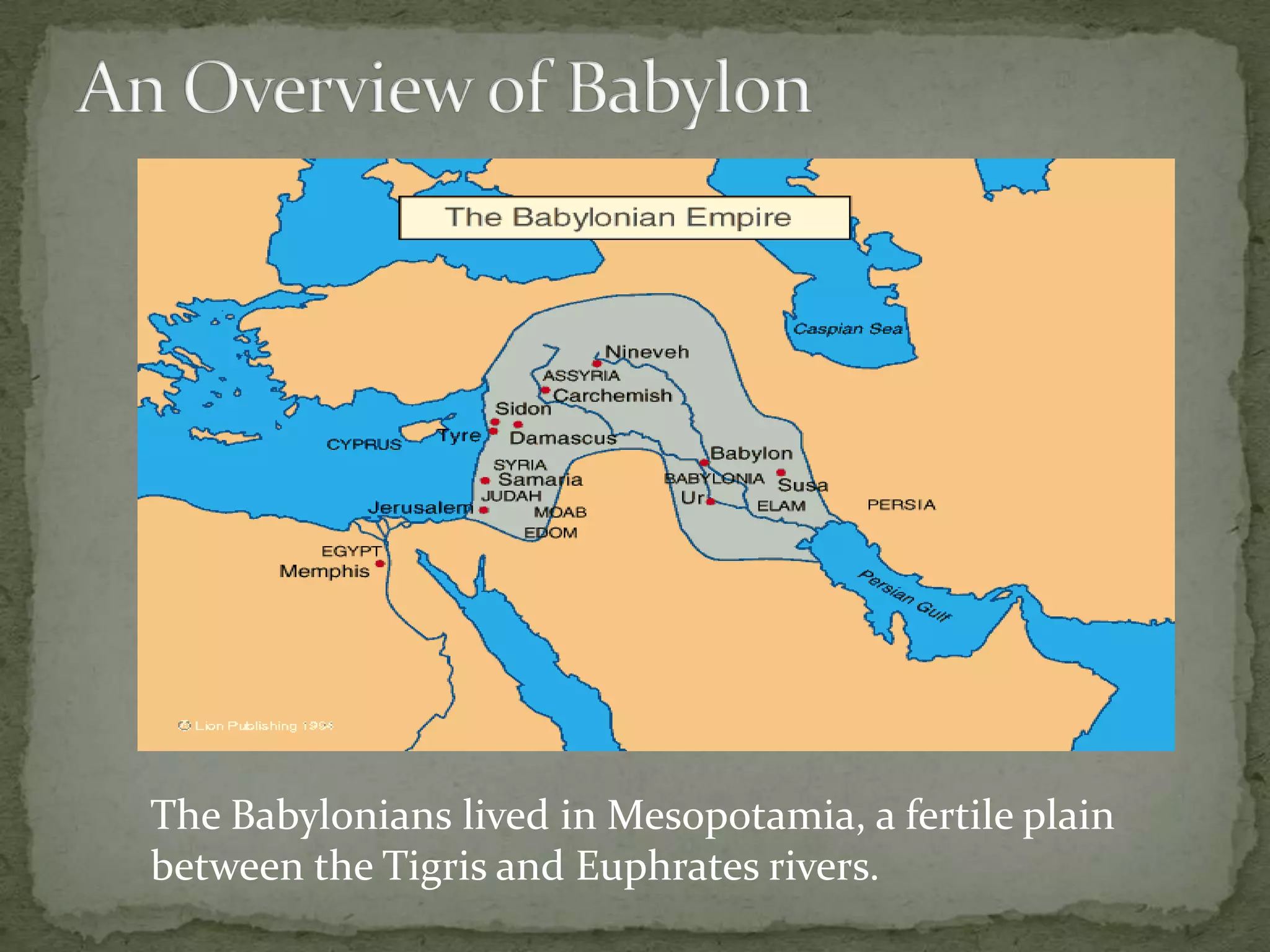
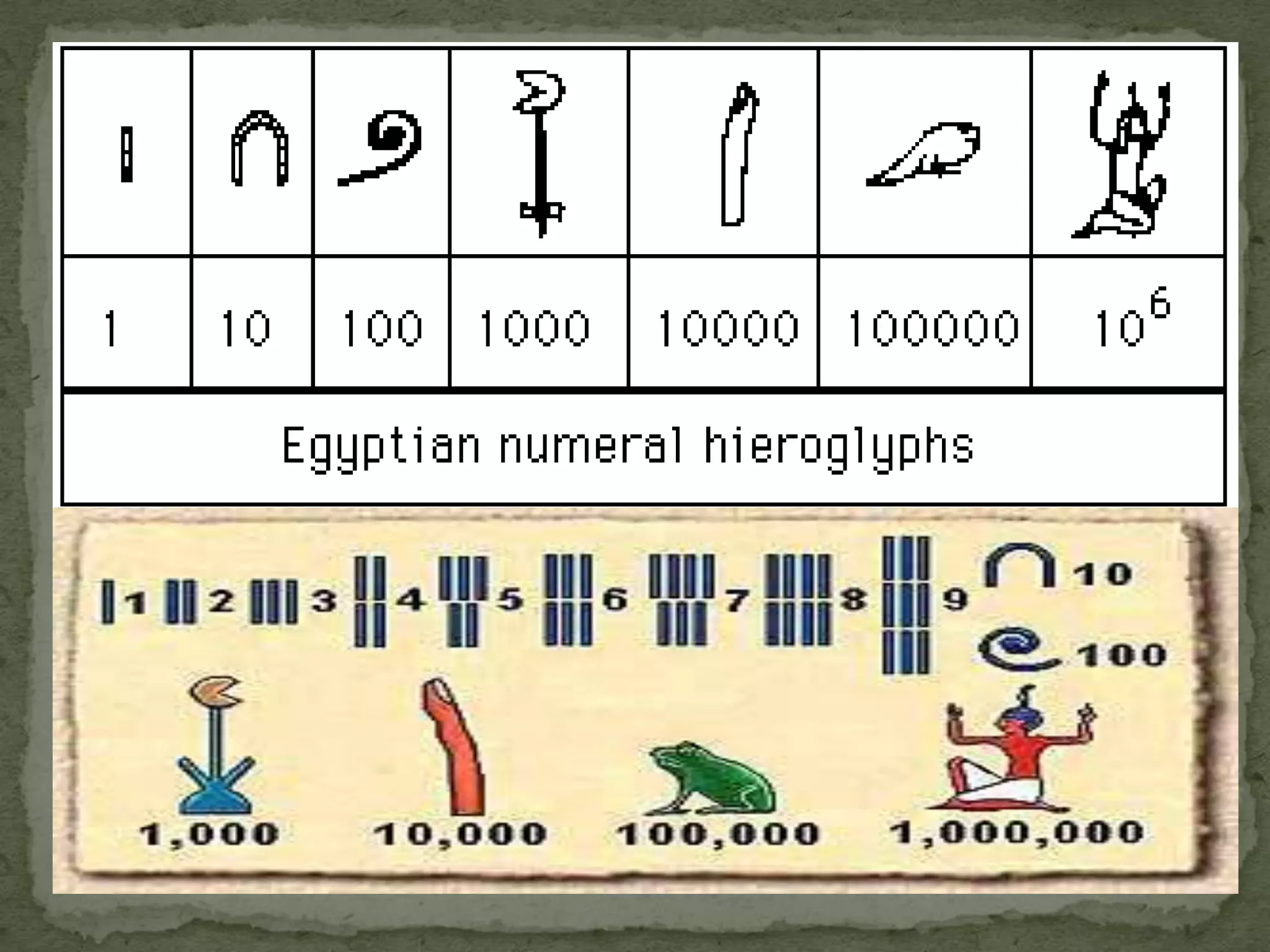
The document discusses mathematics in ancient Babylonian and Egyptian civilizations. It describes how the Babylonians developed a system of writing called cuneiform using wedge-shaped symbols carved into clay tablets around 3000 BC. It also details their sexagesimal (base-60) numerical system and how they were able to perform advanced mathematical operations and solve equations. The document then explains the development of hieroglyphic numerals by the ancient Egyptians, including their base-10 system and specific symbols used to represent fractions and operations. Key sources of information about Babylonian and Egyptian mathematics included cuneiform tablets and Egyptian papyri such as the Rhind Mathematical Papyrus.

1. Babylonian And Egyptian
Mathematics

2. The Babylonians lived in Mesopotamia, a fertile plain
between the Tigris and Euphrates rivers.

3.  The Babylonian civilization has its roots dating to
3500BCE with the Sumerians in Mesopotamia.
 This was an advanced civilization building cities and
supporting the people with irrigation systems, a legal
system, administration, and even a postal service
 The Greeks called this land “Mesopotamia,” meaning
“the land between the rivers.” Most of it today is part of
the modern state of Iraq, although both the Tigris and
the Euphrates rise in Turkey.

4. Babylonian Cuneiform Script

5.  Shortly after 3000 B.C., the Babylonians developed a
system of writing from “pictographs”—a kind of
picture writing much like hieroglyphics.
 Whereas the Egyptians used pen and ink to keep their
records, the Babylonians used first a reed , later a
stylus with a triangular end.
 Because the Latin word for “wedge” is cuneus, the
resulting style of writing has become known as
“cuneiform.”
Triangular
Reed
end

6.  Cuneiform script was a natural consequence of the
choice of clay as a writing medium.
 The stylus did not allow for drawing curved lines, so all
pictographic symbols had to be composed of wedges
oriented in different ways:
 vertical ,
horizontal
 oblique.

8.  Their mathematical notation was positional but
sexagesimal.
 They used no zero.
 More general fractions, though not all fractions, were
admitted.
 They could extract square roots.
 They could solve linear systems.
 They worked with Pythagorean triples.
 They solved cubic equations with the help of tables.
 They studied circular measurement.
 Their geometry was sometimes incorrect.

9.  The Babylonian scale of enumeration was not
decimal, but sexagesimal (60 as a base), so that
every place a “digit” is moved to the left increases
its value by a factor of 60.When whole numbers
are represented in the sexagesimal system, the last
space is reserved for the numbers from 1 to 59, the
next-to-last space for the multiples of 60, preceded
by multiples of 60², and so on.

10. For example, the Babylonian 3 25 4 might stand for the
number
3 · 60² + 25 · 60 + 4 = 12,304
and not
3 · 10³ + 25 · 10 + 4 = 3254,
as in our decimal (base 10) system.
But the question is, how did they find out about the base
sixty numbers?????

11.  It was confirmed by twotablets found in 1854 at
Senkerah on the Euphrates by the English geologist W.
K. Loftus. These tablets, which probably date from the
period of Hammurabi (2000 B.C.), give the squares of
all integers from 1 to 59 and their cubes as far as that of
32.

13. The tablet of squaresreads easily up to 7², or 49. Where we
should expect to find 64, the tablet gives 1 4; the only thing
that makes sense is to let 1 stand for 60. Following 8², the
value of 9² is listed as 1 21, implying again that the left digit
must represent 60. The same scheme is followed throughout
the table until we come to the last entry, which is 58 1,
this cannot but mean:
58 1 = 58 · 60 + 1 = 3481 = 59².

14. But the question now is, how were they able to identify
the translation of the given encryption???

15.  The simple upright wedge had the value 1 and could
be used nine times, while the broad sideways wedge
stood for 10 and could be used up to five times.
 When both symbols were used, those indicating tens
appeared to the left of those for ones, as in

16.  Appropriate spacing between tight groups of symbols
corresponded to descending powers of 60, read from
left to right. As an illustration, we have
 which could be interpreted as
1 · 603 + 28 · 602 + 52 · 60 + 20 = 319,940.

17.  The Babylonians occasionally relieved the
awkwardness of their system by using a subtractive
sign . It permitted writing such numbers as 19 in
the form 20 − 1,
instead of using a tens symbol followed by nine units:

18.  Babylonian positional notation in its earliest
development lent itself to conflicting interpretations
because there was no symbol for zero. There was no
way to distinguish between the numbers
1 · 60 + 24 = 84 and 1 · 602 + 0 · 60 + 24 = 3624,
since each was represented in cuneiform by

19.  Because of this problem in the positional system, in
300 B.C. a new symbol was developed called he
placeholder represented by
or

20.  With this, the number 84 was readily distinguishable
from 3624, the latter being represented by

21.  The absence of zero signs at the ends of numbers meant
that there was no way of telling whether the lowest place
was a unit, a multiple of 60 or 60², or even a multiple of
1/60 . The value of the symbol 2 24 in cuneiform
could be
2 · 60 + 24 = 144.
but other interpretations are possible, for instance,
2 · 60² + 24 · 60 = 8640,
or if intended as a fraction,
2 + 24/60 = 2/25 .

22. The square root of √2, the length of the diagonal of a unit
square was approximated by the babylonians of the Old
Babylonian Period (1900 B.C.-1650 B.C.) as
24 51 10 30547
1: 24:51:10 1 2 3
1.414212.....
60 60 60 21600

23. Thus, the Babylonians of antiquity never achieved
an absolute positional system. Their numerical
representation expressed the relative order of the
digits, and context alone decided the magnitude of a
sexagesimally written number; since the base was so
large, it was usually evident what value was intended.

25. Hieroglyphic Representation of Numbers

26.  Civilisation reached a high level in Egypt at an early
period. The country was well suited for the people,
with a fertile land thanks to the river Nile yet with a
pleasing climate. It was also a country which was easily
defended having few natural neighbours to attack it
for the surrounding deserts provided a natural barrier
to invading forces. As a consequence Egypt enjoyed
long periods of peace when society advanced rapidly.

27.  By 3000 BC two earlier nations had joined to form a
single Egyptian nation under a single ruler. Agriculture
had been developed making heavy use of the regular
wet and dry periods of the year. The Nile flooded
during the rainy season providing fertile land which
complex irrigation systems made fertile for growing
crops. Knowing when the rainy season was about to
arrive was vital and the study of astronomy developed
to provide calendar information.

28.  Hieroglyphs are little pictures representing words. It is
easy to see how they would denote the word "bird" by a
little picture of a bird but clearly without further
development this system of writing cannot represent
many word.
 The Egyptians had a bases 10 system of hieroglyphs for
numerals. By this we mean that they has separate
symbols for one unit, one ten, one hundred, one
thousand, one ten thousand, one hundred thousand,
and one million.

30. 1. The RhindMathematical Papyrus named for
A.H.Rhind (1833-1863) who purchased it at Luxor in
1858. Origin: 1650 BCE but it was written very much
earlier. It is 18 feet long and13 inches wide. It is also
called the Ahmes Papyrus after the scribe that last
copied it.
 The Moscow Mathematical Papyrus purchased by V. S.
Golenishchev (d. 1947). Origin: 1700 BC. It is 15 ft long
and 3 inches wide. Two sections of this chapter offer
highlights from these papyri.

32.  Multiplication is basically binary.
Example Multiply: 47 × 24
47 × 24
47 1
94 2
188 4
376 8*
752 16 *
 Selecting 8 and 16 (i.e. 8 + 16 = 24), we have
24 = 16 + 8
47 × 24 = 47 × (16 + 8)
= 752 + 376
= 1128

34.  Although the Egyptians had symbols for
numbers, they had no generally uniform notation for
arithmetical operations. In the case of the famous
Rhind Papyrus (dating about 1650 B.C.),the scribe did
represent addition and subtraction by the hieroglyphs
and , which resemble the legs of a person coming
and going.

36.  The symbol for unit fractions was a flattened oval
above the denominator. In fact, this oval was the sign
used by the Egyptians for the mouth .
 For ordinary fractions, we have the following.
1 1
3 1
7
24

37.  There were special symbols for the fractions 1/2 , 2/3 ,
3/4, of whichone each of the forms is shown below.
1
2 3
2 3 4

39.  Burton, David (2007) The History of Mathematics:
An Introduction, Sixth Edition, Page 12-28
 MacTutor, Babylonian and Egyptian Numerals
 http://en.wikipedia.org/wiki/Babylonian_numerals