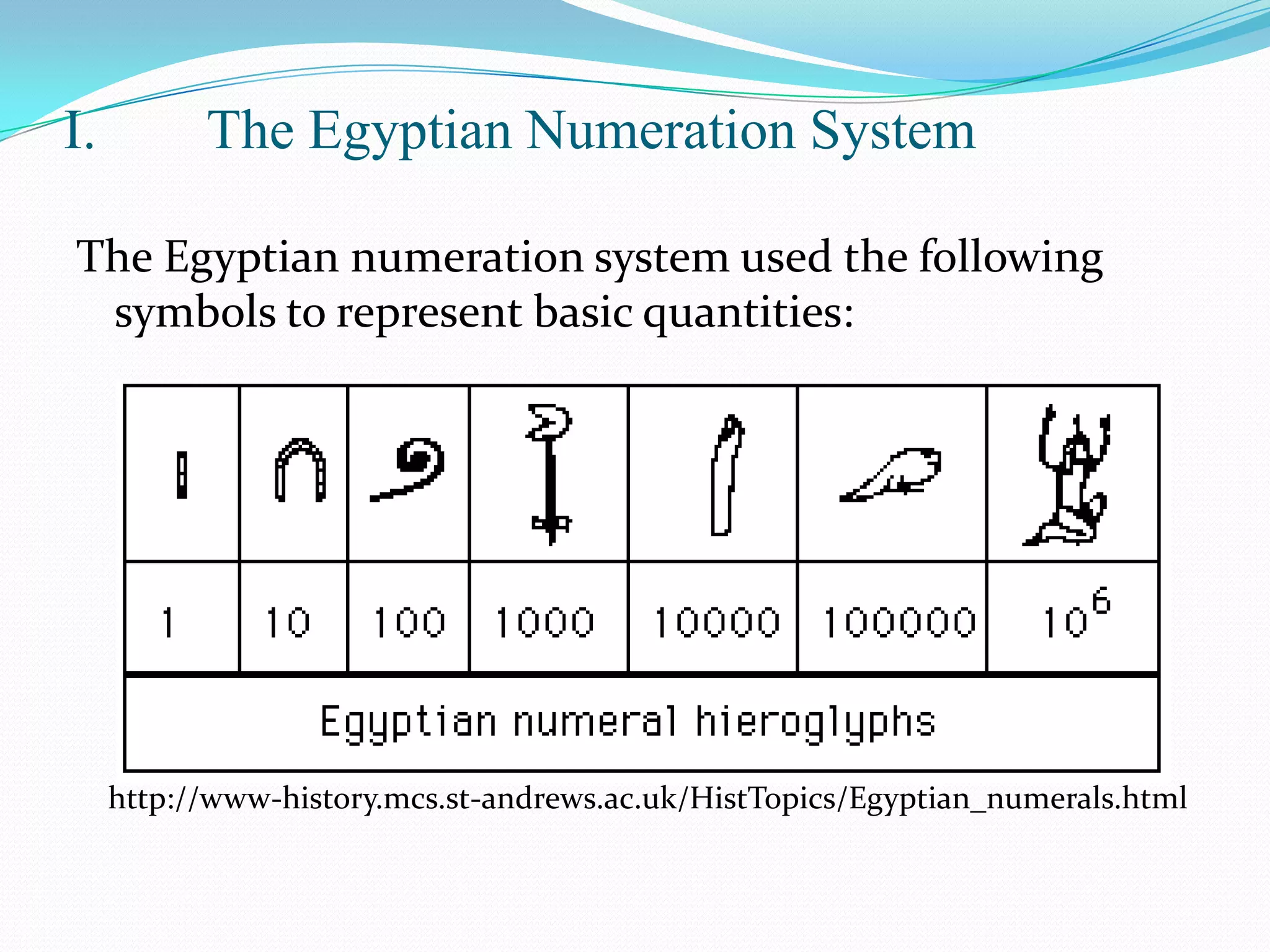
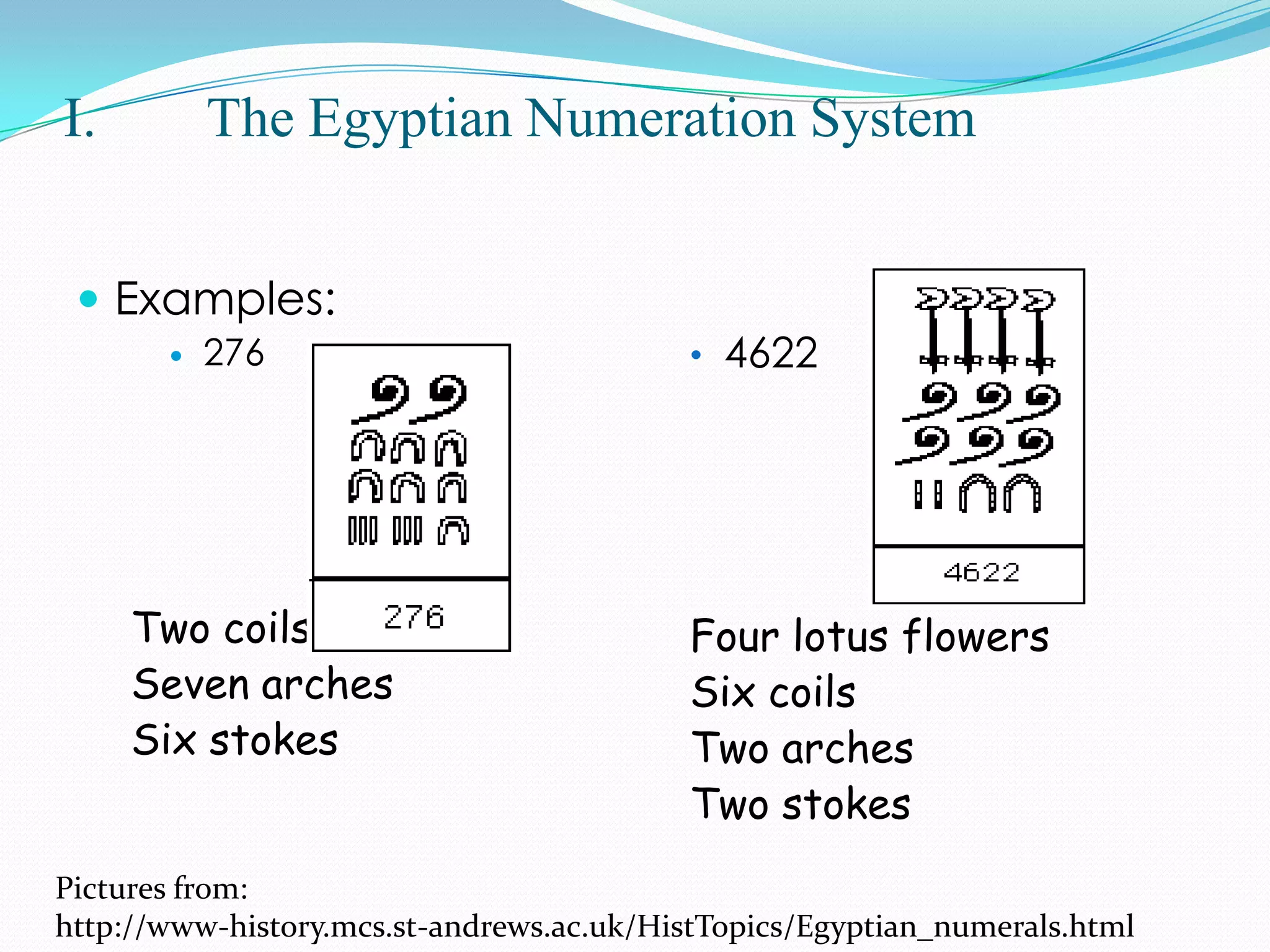
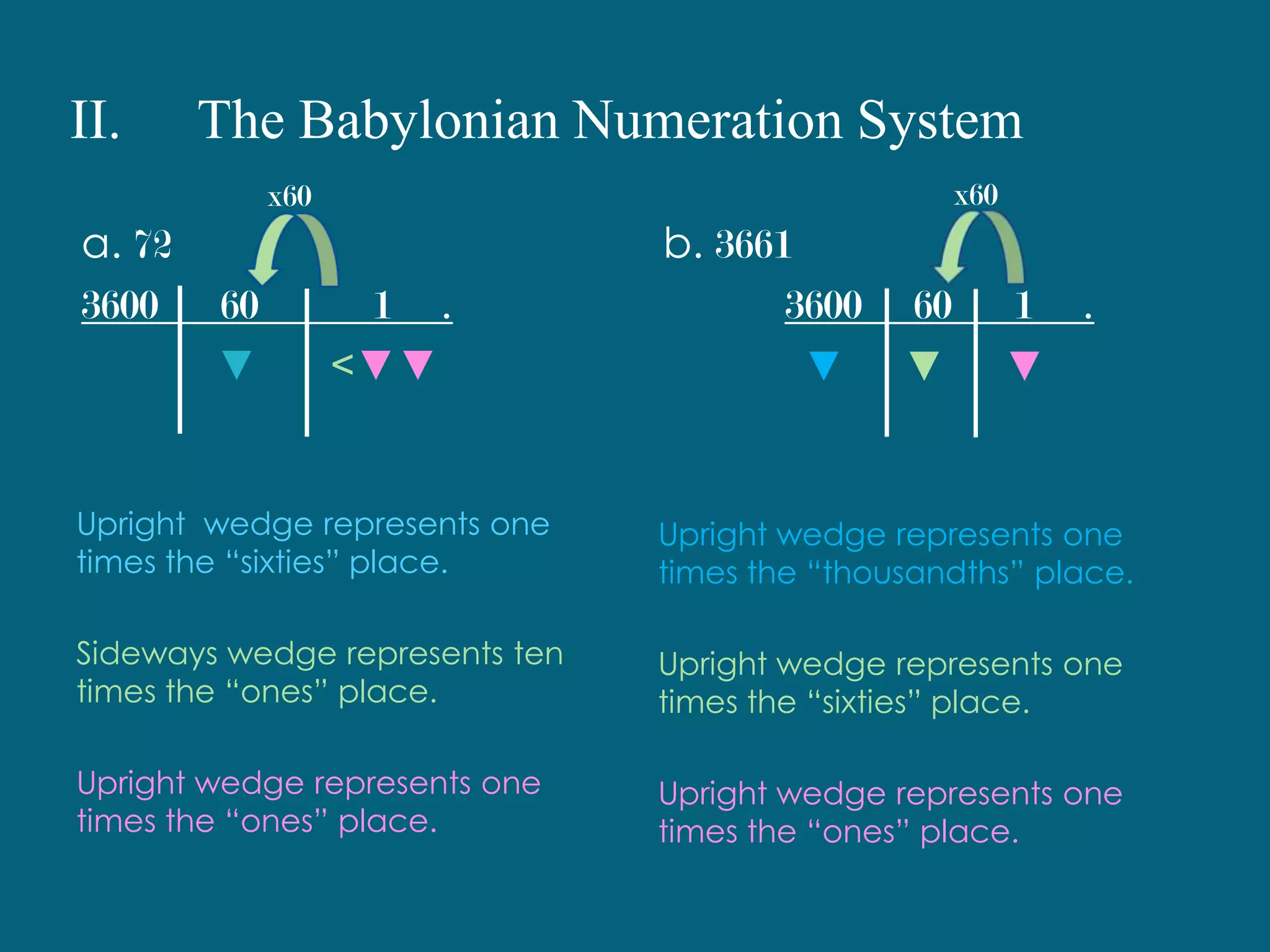
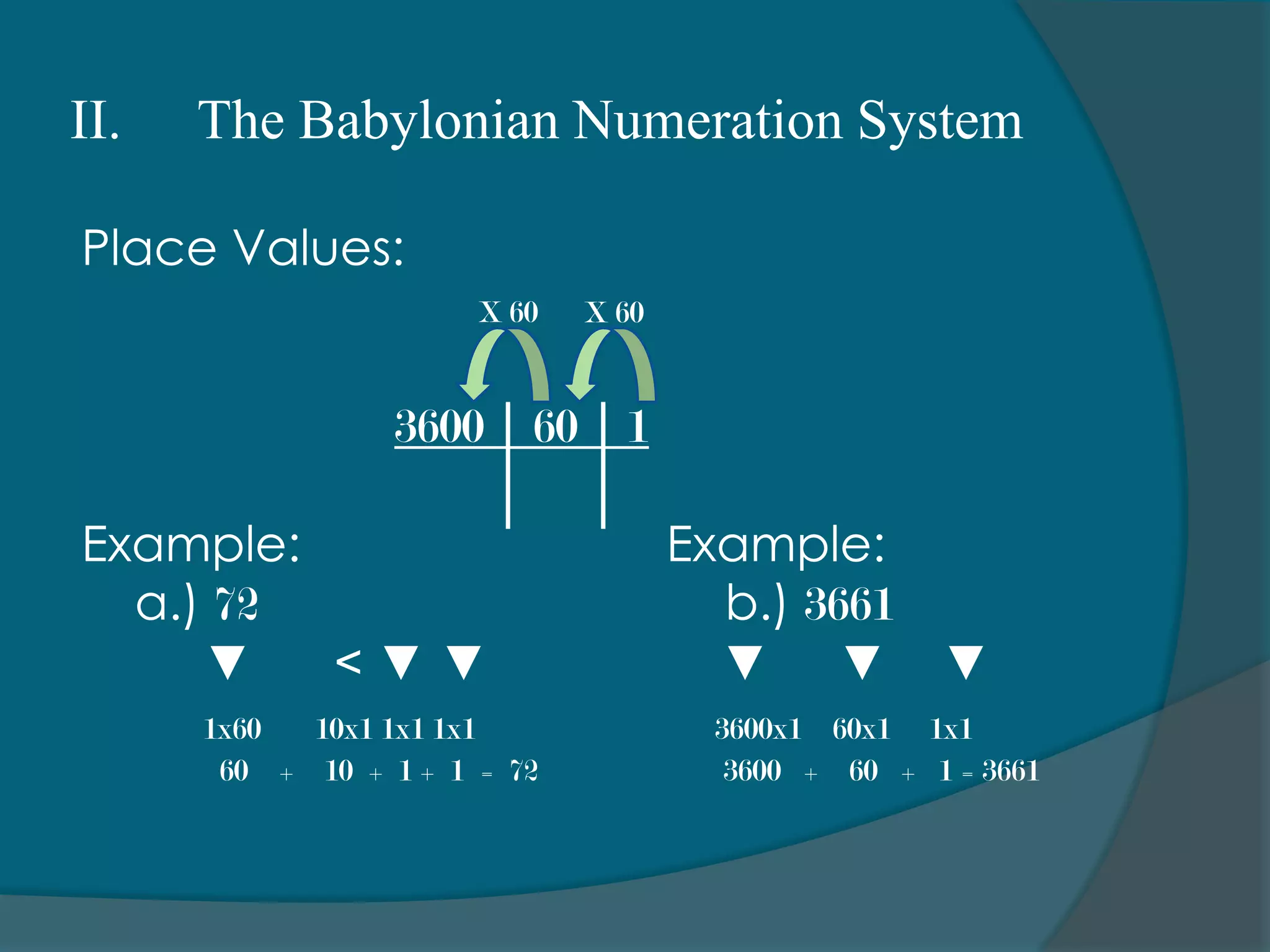
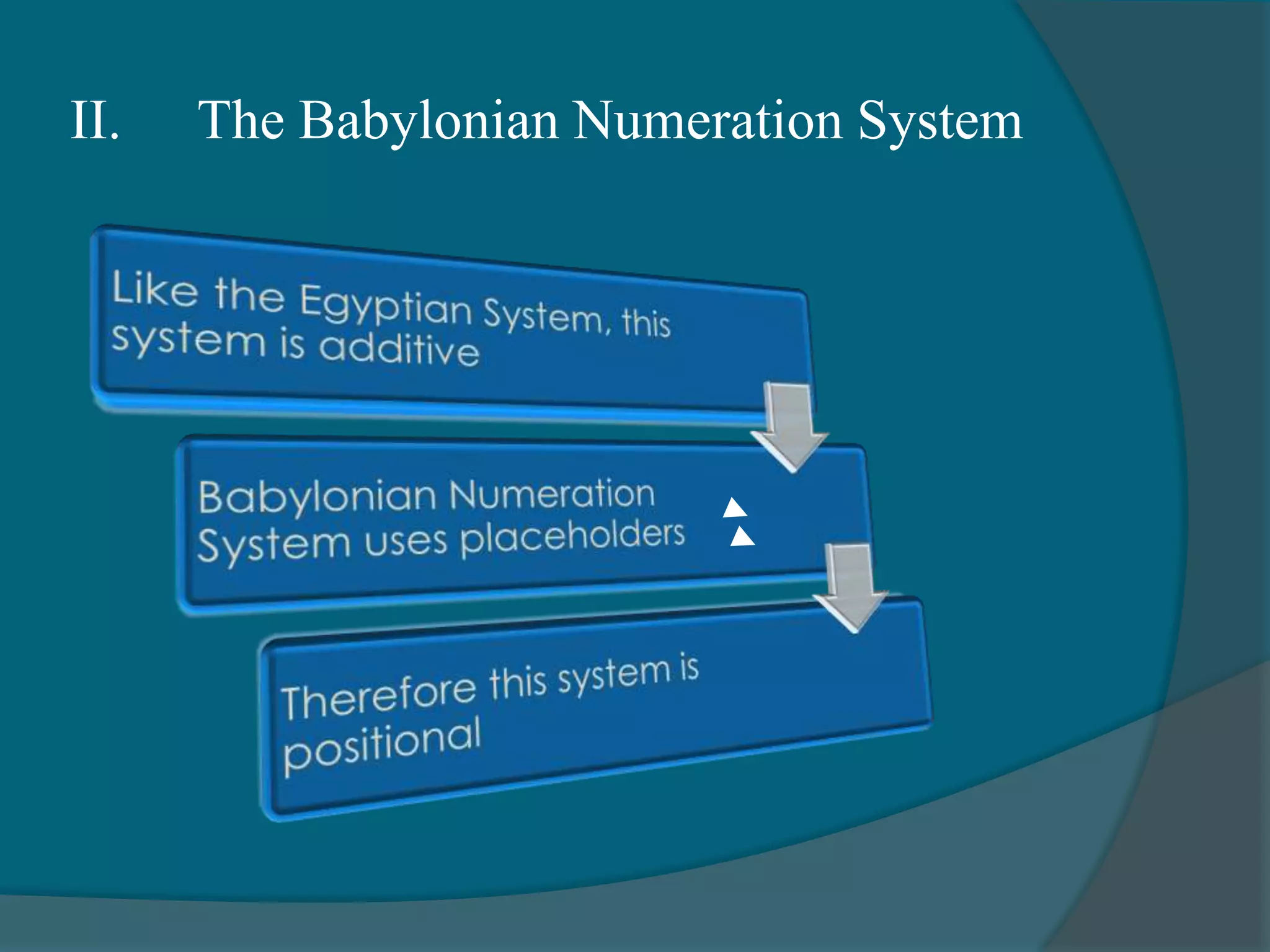
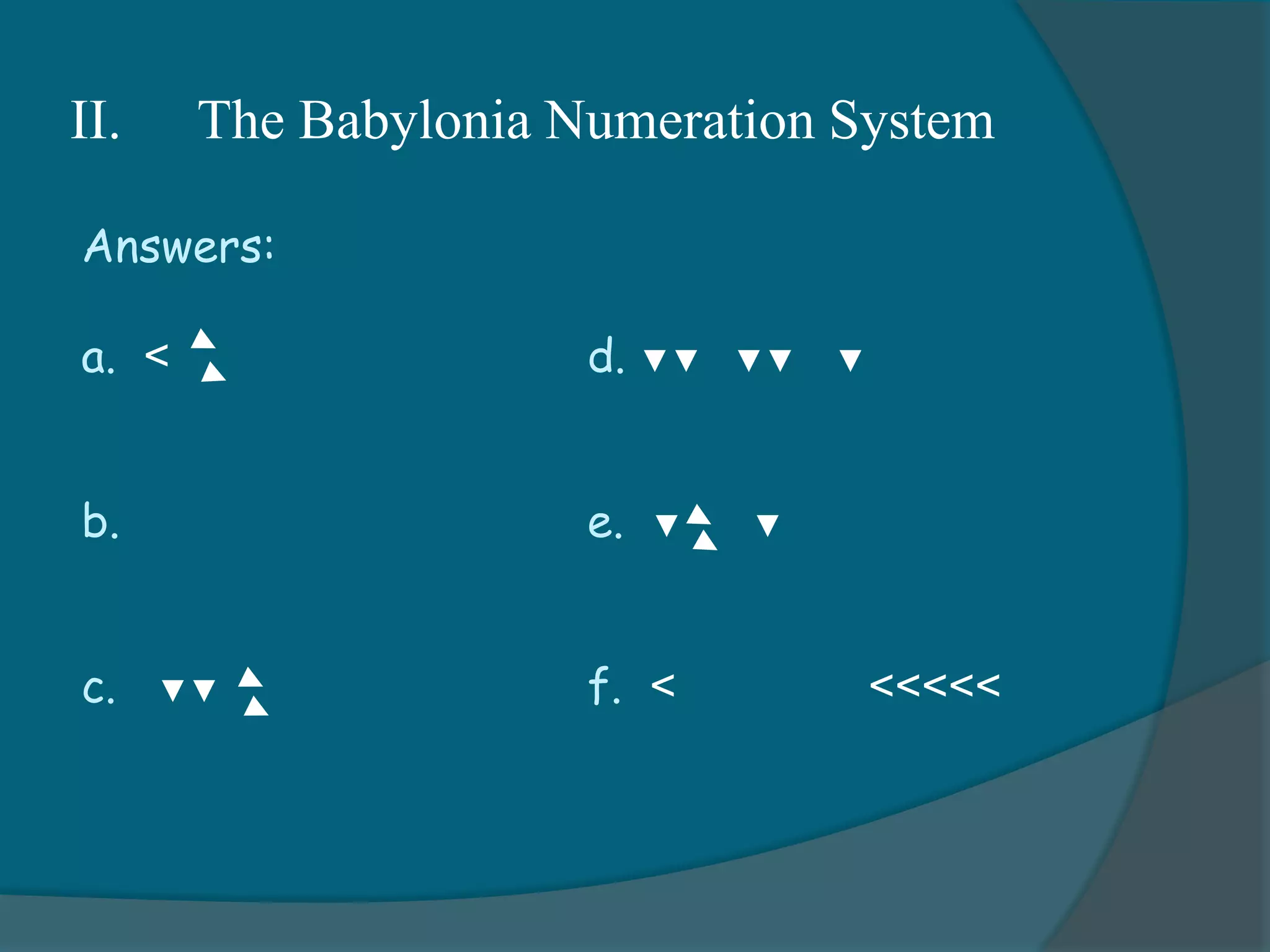
The document discusses three ancient numeration systems: 1) The Egyptian system used hieroglyphic symbols like strokes, arches, and coils in an additive-only system. 2) The Babylonian system introduced place value using upright and sideways wedges to represent values of 60 and its powers. 3) The Roman system used symbols like I, V, X, L, C, D, and M in an additive and subtractive system based on symbol position.

1. Numeration SystemsBy: Lindsay FredericksOctober 5th, 2010EDU 290T&TH 8:00am

2. Three Basic Numeration SystemsThe Egyptian Numeration SystemThe Babylonian numeration SystemThe Roman Numeration System

3. The Egyptian Numeration System

4. The Egyptian Numeration SystemThe Egyptian numeration system used the following symbols to represent basic quantities:http://www-history.mcs.st-andrews.ac.uk/HistTopics/Egyptian_numerals.html

5. They Egyptian Numeration1 = Stroke10 = Arch100= Coiled Rope (Coil)1,000= Lotus Flower10,000 = Pointed Finger100,000 = Tadpole1,000,000 = Man with Arms Raised

6. The Egyptian Numeration SystemThis system is a strictly additional system. There are multiple ways to represent quantities. 221 could be written : 1+10+10+100+100, or 1+100+10+100+10using the symbols.

7. This was probably confusing.Multiple representations were used up until the twenty-seventh century BCE when it became more typical to write basic symbols in descending order.Because strictly addition, simple matter of styleThe Egyptian Numeration SystemExamples: 276Two coilsSeven archesSix stokes4622 Four lotus flowersSix coils Two archesTwo stokesPictures from:http://www-history.mcs.st-andrews.ac.uk/HistTopics/Egyptian_numerals.html

8. The Egyptian System RecapEgyptians used symbol: Hieroglyphics

9. The numerations system is strictly additive, descending order.

10. Carved symbols into monuments.

11. There are seven symbols used in the system (stoke, arch, coil, lotus flower, pointed finger, tadpole, and man with raised arms)II.The Babylonian Numeration SystemMathematicians and astronomers of Babylon developed a numeration system based on much older system inherited from the Sumerians.There were two basic symbols used 1. Upright wedge – representing one (1) ▼ 2. Sideways wedge – representing ten (10) <

12. II. The Babylonian Numeration SystemExamples:a.) 32 <<<▼▼b.) 5 ▼▼▼▼▼c.) 12 <▼▼

13. II. The Babylonian Numeration SystemOnce the quantity being represented reached sixty this became a group. In a new place, ▼ represents not one, but one group of sixty (hence place values).In a new place, < represents not ten, but ten groups of sixty.“sixties place”

14. II. The Babylonian Numeration Systemx60x60a. 723600 60 1 . ▼<▼▼b. 36613600 60 1 .▼▼▼Upright wedge represents one times the “sixties” place.Sideways wedge represents ten times the “ones” place.Upright wedge represents one times the “ones” place.Upright wedge represents one times the “thousandths” place. Upright wedge represents one times the “sixties” place.Upright wedge represents one times the “ones” place.

15. II. The Babylonian Numeration System“Think of time. we write nine fifty-nine as 9:59. What happens when another minute passes? we DON’T write 9:60. Instead , we think of those sixty minutes as one hour (one group of sixty minutes) the nine increases by one.So, we write 10:00. Meaning ten hours and no leftover minutes.”

16. II. The Babylonian Numeration SystemPlace Values:3600 60 1 Example: Example: a.) 72 b.) 3661 ▼ < ▼ ▼ ▼ ▼ ▼1x60 10x1 1x1 1x1 3600x1 60x1 1x1 60 + 10 + 1 + 1 = 72 3600 + 60 + 1 = 3661X 60X 60

17. II. The Babylonian Numeration SystemThere is some confusion when leaving spaces

18. Deciding whether it’s in the “sixties” place or the “thousandths” place.

19. New Symbol for this “empty space”Example: 36013600 60 1 . = 3601 ▼ ▼ ▼ ▼Instead of: ▼ ▼►►►►►►

20. II. The Babylonian Numeration System►►

21. II. The Babylonian Numeration System Let try some!a. 600b. 62c. 120d. 7321e. 3601f. 832

22. II. The Babylonia Numeration SystemAnswers:a. <b. ▼ ▼▼c. ▼▼ d. ▼▼ ▼▼ ▼e. ▼ ▼ f. < ▼▼▼ <<<<<▼▼►►►►►►

23. III. The Roman Numeration SystemIncludes the following symbols:I = [1] M = [1000]V = [5] V = [5000]X = [10] X = [10000]L = [50]C = [100]D = [500]

24. III. The Roman Numeration systemThis system is additive-to create 6 -add V and I : VITry one-create 12Answer: XII

25. III. The Roman Numeration SystemThis system is also subtractive - to create 9-place I in front of X: IX* Smaller number in front of the larger number to subtractTry one-create 499Answer: ID

26. III. The Roman Numeration SystemTo Review. This system is both additive, and subtractive.

27. Because of the placement of the symbols matters the system is positionalA few more examples:a. CLVI c. MMDCCCLVIb. CDLXI d. DXVII

28. III. The Roman Numeration SystemAnswers:CLVI = 156c = 100+ L =50+ V =5+ I =1CDLXI = 461C= 100 - D= 500 + L= 50 + X= 10 + I = 1MMDCCCLVI = 2,856(M=1000)+(M=1000)+(D=500)+(C=100)+(C=100) +(C=100)+(L=50)+(V=5)+(I=1)DXVII = 517(D = 500) + (X = 10) + (V = 5) + (I = 1) + (I = 1)

29. The ENDReferences: Dr. Christine PhelpsFall 2010MTH 151Central Michigan University Course # 22129396Pictures on slide seven fromhttp://www-history.mcs.st-andrews.ac.uk/HistTopics/Egyptian_numerals.html Pictures on slide four from http://www-history.mcs.st-andrews.ac.uk/HistTopics/Egyptian_numerals.html