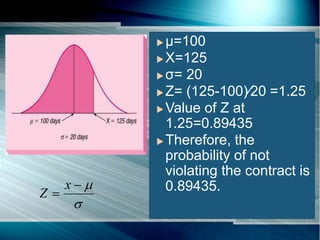
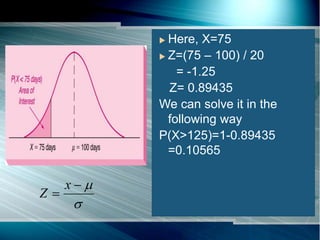
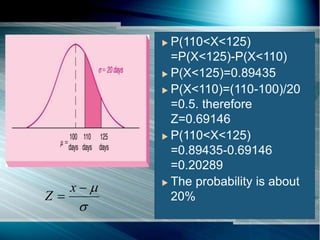
The document discusses the normal probability distribution and its characteristics. It then provides an example of a construction company that builds triplexes and quadraplexes. The time to construct a triplex follows a normal distribution with a mean of 100 days and standard deviation of 20 days. The document calculates the probability that the construction company will complete a triplex within the contracted time of 125 days, which is about 89%. It also calculates the probability of completing a triplex in under 75 days to receive a bonus, which is about 11%, and the probability of completing it between 110-125 days, which is about 20%.

2.  Normal probability distribution or
commonly called the normal
distribution is one of the most
important continuous theoretical
distributions in statistics.
 Most of the data relating to
economics and business statistics or
even in social and physical sciences
conform to this distribution.

4. Characteristics
 The curve is symmetrical and bell
shaped.
 It is continuous for all values of X
between -∞ and ∞.

5.  Since the distribution is symmetrical,
mean, median, mode coincide. Thus,
Mean=Median=Mode.
 No portion of the curve lies below the
x-axis, since p(x) being the probability
can never be negative

7.  Haynes Construction Company builds
primarily triplexes and quadraplexes for
investors, and it is believed that the total
construction time in days follows a normal
distribution. The mean time to construct a
triplex is 100 days, and the standard
deviation is 20 days. Recently, the
president of Haynes Construction signed
a contract to complete a triplex in 125
days.

8. Failures to complete the triplex in 125
days would result in severe penalty fees.
What is the probability that Haynes
Construction will not be in violation of their
construction contract?

9.  µ=100
 X=125
 σ= 20
 Z= (125-100)∕20 =1.25
 Value of Z at
1.25=0.89435
 Therefore, the
probability of not
violating the contract is
0.89435.



x
Z

10.  If the firm finishes these
triplexes in 75 days or
less, it will be rewarded
a bonus payment of
$5000. What is the
probability that Haynes
will receive the bonus?

11.  Here, X=75
 Z=(75 – 100) / 20
= -1.25
Z= 0.89435
We can solve it in the
following way
P(X>125)=1-0.89435
=0.10565



x
Z

12. What is the
probability that
the triplex will
take between 110
and 125 days?

13.  P(110<X<125)
=P(X<125)-P(X<110)
 P(X<125)=0.89435
 P(X<110)=(110-100)/20
=0.5. therefore
Z=0.69146
 P(110<X<125)
=0.89435-0.69146
=0.20289
 The probability is about
20%



x
Z