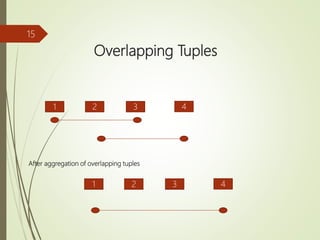
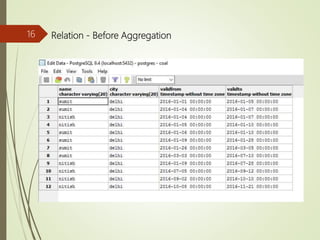
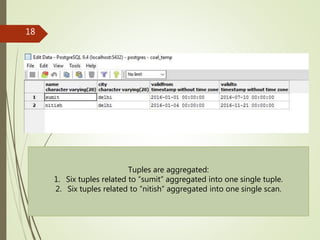
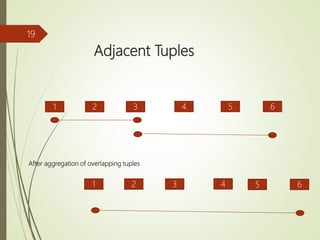
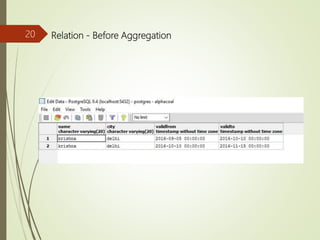
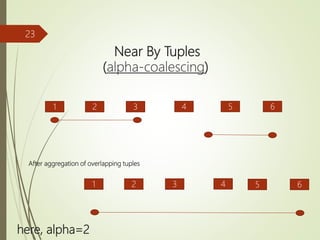
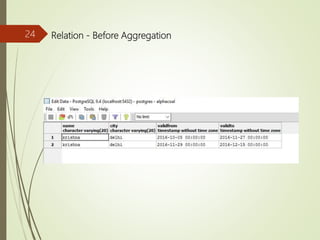
The document presents a study on implementing temporal aggregation functions through user defined aggregate (UDA) functions. It discusses aggregating tuples that are adjacent, overlapping, or near each other in timestamp. Algorithms are presented for aggregating adjacent tuples, overlapping tuples, and near by tuples within a threshold. The algorithms perform aggregation by scanning the relation once. Literature on parsimonious temporal aggregation and supporting temporal queries efficiently in databases is also summarized.

1. Presentation
on
STUDY AND IMPLEMENTATION OF
TEMPORAL AGGREGATION FUNCTIONS
PRESENTED BY:
NITISH SHARMA
SUPERVISED BY:

2. Objective
 To study various techniques of Temporal Aggregation.
 To implement User Defined Aggregate functions (UDA) for adjacent, overlapping
or near by tuples.
2

3. Base Paper
Title: Parsimonious Temporal Aggregation
Author(s): Juozas Gordeviˇcius · Johann Gamper · Michael Böhlen
The VLDB Journal (2012) 21:309–332
DOI : 10.1007/s00778-011-0243-9
3

4. Temporal aggregation merges the temporal extents of value-equivalent
tuples. A temporal extent is usually coalesced offline and stored since
aggregation is an expensive operation.
• User defined aggregates (UDA) function are developed for the
aggregation of tuples with adjacent, overlapping or near by timestamps
through which the temporal aggregation process becomes stress-free
operation in temporal database.
 the underlying temporal data model supports tuple time-stamping and
the valid time.
 the insert and the update operations preserve the temporal order of
tuples in the modeled reality.
4

5. Introduction
Temporal aggregation is used to summarize large sets of such data by aggregating
specific attribute values over all tuples that hold at a time point or a time interval.
Aggregation Types:
• In instant temporal aggregation (ITA) the aggregate value at a time instant t is
computed from the set of all tuples whose timestamp contains t.
• Span temporal aggregation (STA) - allows an application to specify in the query
the time intervals for which to report result tuples
5

6. Candidates for Temporal Aggregation
 Adjacent Tuples
 Near-by Tuples
 Overlapping Tuples
6

7. Definition
• Adjacent tuples
Let s be a sequential relation with schema
S = (A1, . . . , Ak , B1, . . . , Bp, T)
&
grouping attributes A = {A1, . . . , Ak }.
Two tuples si , s j ∈ s are adjacent, si ≺ s j , iff the following holds:
(1) si .A = s j .A,
(2) si .te = s j .tb − 1.
7

8. Contd.
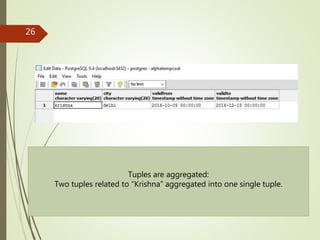
• Merge operator
Let s be an ITA result relation with schema
S = (A1, . . . , Ak , B1, . . . , Bp, T), where
A = {A1, . . . , Ak } are the grouping attributes and
B = {B1, . . . , Bp} store the aggregate values.
The merge, ⊕, of two adjacent tuples, si , s j ∈ s, si ≺ s j , is defined as
si ⊕ s j = (si .A1, . . . , si .Ak, v1, . . . , vp, [si .Tb, s j .Te]),
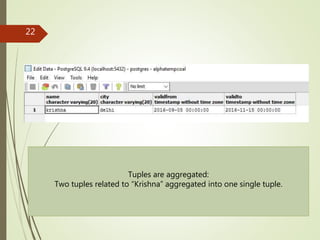
The merge operator produces a new tuple.
8

9. Problems in Temporal Aggregation operation
 A projection of a coalesced temporal relation may produce an un-
coalesced result
 Update and Insert operations may not enforce coalescing due to
efficiency concerns
 Time union operators cannot be expressed in terms of traditional
relational algebra
9

10. Temporal Aggregation approaches
• Run-time:
During execution of query, tuples are coalesced as needed
• Insert:
During insertion of tuple in the relation
• Update:
Tuples are coalesced, when existing data is modified
10

11. User Defined Aggregates (UDA)
• UDA is a native SQL extension.
• UDAs can be used to support windows, time-series queries, and
sequence queries on data streams.
• UDA approach beats the traditional pure SQL coalescing queries in
performance.
• UDA, requires one single scan of the input tuples.
11

12. Algorithm
“User Defined Aggregate function for aggregation of adjacent or overlapping tuples”.
1: Define table Temp (TSTART, TEND) to store the current coalesced period, initially
empty;
2: Insert the first tuple’s TSTART and TEND value into Temp;
3: for every new input tuple T do
4: if T.TSTART <= Temp.TEND then
5: //new tuple coalescable with current period
6: Update Temp.TEND with T.TEND;
7: else
8: //current coalesced period ends, a new coalescing period begins
9: Output the tuple in Temp, then update Temp with T.TSTART and T.TEND;
10: end if
11: end for
12: Output the tuple in Temp;
12

13. Algorithm
“User Defined Aggregate function for aggregation of near by tuples”.
STEPS:
Input: A nearby threshold α; a sorted list of intervals S = {s1, s2, • • • , sm}
Output: A list of coalesced intervals T
1: T ← ∅
2: t ← s1 #t is a working variable for intermediate coalescing result
3: i ← 2
4: while i <= |S| do
5: if si.B > t.E + α ∨ si.W ≠ t.W then #not α-coalescible
6: T ← T ∪ {t}
7: t ← si
8: else if si.E > t.E ∧ si.W = t.W then #coalesce
9: t.E ← si.E
10: end if
11: i ← i + 1.
12: end while
13: return T
13

14. Screenshots
14

15. Overlapping Tuples
15
1 2 3 4
After aggregation of overlapping tuples
1 2 3 4

16. Relation - Before Aggregation16

17. Relation - After Aggregation of Tuples
17

18. 18
Tuples are aggregated:
1. Six tuples related to “sumit” aggregated into one single tuple.
2. Six tuples related to “nitish” aggregated into one single scan.

19. Adjacent Tuples
19
1 2 3 4
After aggregation of overlapping tuples
1 2 3 4
5 6
5 6

20. Relation - Before Aggregation20

21. Relation - After Aggregation of Tuples
21

22. 22
Tuples are aggregated:
Two tuples related to “Krishna” aggregated into one single tuple.

23. Near By Tuples
(alpha-coalescing)
23
1 2 3 4
After aggregation of overlapping tuples
1 2 3 4
5 6
5 6
here, alpha=2

24. Relation - Before Aggregation24

25. Relation - After Aggregation of Tuples
25

26. 26
Tuples are aggregated:
Two tuples related to “Krishna” aggregated into one single tuple.

27. Literature Survey
Parsimonious temporal aggregation[1].
A novel temporal aggregation operator, termed parsimonious temporal
aggregation (PTA), that overcomes major limitations of existing approaches. PTA
takes the result of instant temporal aggregation (ITA) of size n, which might be up
to twice as large as the argument relation, and merges similar tuples until a given
error (e) or size (c) bound is reached. The new operator is data-adaptive and allows
the user to control the trade-off between the result size and the error introduced
by merging. For the precise evaluation of PTA queries, we propose two dynamic
programming-based algorithms for size and error-bounded queries, respectively,
with a worst-case complexity that is quadratic in n. For the quick computation of
an approximate PTA answer, we propose an efficient greedy merging strategy with
a precision that is upper bounded by O(log n). We present two algorithms that
implement this strategy and begin to merge as ITA tuples are produced. They
require O(n log(c + β)) time and O(c + β) space, where β is the size of a read-ahead
buffer and is typically very small.
27

28. Contd.
Efficient temporal coalescing query support in relational database systems[3].
An SQL: 2003-based query algorithm and a native relational user defined
aggregates (UDA) approach – both approaches only require a single scan of the
database. They conclude that temporal queries can be best supported by OLAP
functions supported in the current SQL: 2003 standards. These new findings
demonstrate that the current RDBMSs are mature enough to directly support
efficient temporal queries, and provide a new paradigm for temporal database
research and implementation.
28

29. Conclusion
• User defined aggregates (UDA) are developed for the aggregation of
tuples with adjacent, overlapping or near by timestamps through
which the temporal aggregation process becomes stress-free
operation in temporal database. Two additional tracing attributes are
associated with each temporal attribute of a relation which are used
to trace the change in value of the corresponding temporal attribute.
• UDA approach beats the traditional pure SQL coalescing queries in
performance.
29

30. Future work
Try to optimize cost of temporal aggregate operator.
30

31. Reference
[1] Gordevičius, Juozas, Johann Gamper, and Michael Böhlen. "Parsimonious temporal
aggregation." The VLDB Journal 21.3 (2012): 309-332.
[2] Pilman, Markus, et al. "ParTime: Parallel Temporal Aggregation." Proceedings of the 2016
International Conference on Management of Data. ACM, 2016.
[3] Zhou, Xin, Fusheng Wang, and Carlo Zaniolo. "Efficient temporal coalescing query support
in relational database systems." International Conference on Database and Expert Systems
Applications. Springer Berlin Heidelberg, 2006.
[4] Cheng, Kai. "Approximate Temporal Aggregation with Nearby Coalescing." International
Conference on Database and Expert Systems Applications. Springer International Publishing,
2016.
31