Temporal PPT details about the platform and its uses

Temporal Databases
S. Srinivasa Rao
April 12, 2007
[Part 1 based on Ch23 of C.J. Date (slides by Prof. Ghafoor, EE 562)]
[Part 2 based on slides by Prof. Arge, I/O-algorithms]

2
Outline
• Part 1: Introduction to temporal databases
• Part 2: Temporal index: Persistent B-tree and its applications

3
Introduction
• Temporal database: a database that contains historical data as well
as current data.
– Note: ‘historical’ is a misleading term – temporal databases may contain
data regarding the future as well as the past.
• Extreme case: data is only inserted, never deleted from a temporal
database (eg. vehicle position data in the ‘project’).
• So far, we have studied the other extreme - i.e. ‘snapshot’ databases.
• Distinguishing feature: the element of time.

4
Introduction
• Temporal data: encoded representation of timestamped facts.
– Each tuple must include at least one timestamp.
– Problem:What about queries that produce results that are not
temporal? i.e. result of query is outside the domain of (temporal)
database.
– eg. Get names of all people who have supplied something in the
past.
• Redefine temporal database: database that includes, but is not
limited to, temporal data.

5
Motivation
• Queries on time-varying data are difficult to express in SQL.
• Temporal databases provide build-in support for recording and
querying such information.
• It is possible to use SQL to evaluate these queries, but performance
is poor.

6
Motivation
• Most applications manage temporal data.
• If a temporal database is used for such data:
– Schemas, including integrity constraints are simpler.
– Queries are simpler
• Application code is less complex
– easier to understand
– easier to produce
– easier to maintain

7
Applications
Most applications of database technology are temporal in nature:
• Financial apps.: portfolio management, accounting & banking, stock
market analysis, audit analysis
• Record-keeping apps.: personnel, medical records, inventory management,
legal records (commercial laws change frequently)
• Data Warehousing: historical trends for analysis
• Scheduling apps.: airline, car, hotel reservations and project management
• Scientific apps.: weather monitoring, chemical process monitoring

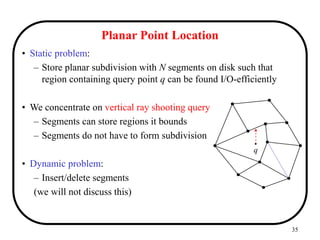
8
Intervals
• An interval [s,e] is a set of times from time s to time e.
– Does interval [s,e] represent an infinite set?
– Assumption: Timeline is a finite sequence of discrete, indivisible
time quanta.
• Time Quanta: smallest unit of time system can represent.
• Timepoints/point: time unit considered indivisible for our purpose.
• An interval is treated as a single type, not as pair of separate values.
• Interval can be open/closed w.r.t. start point/end point.
– eg. [d04,d10],[d04,d11),(d03,d10],(d03,d11)
all represent the sequence of days from day4 to day10 inclusive.

9
Operators on Intervals
• Temporal predicate operators:
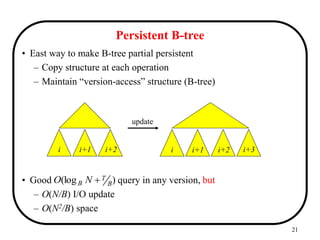
i1 = [s1,e1]; i2 = [s2,e2]
– i1 BEFORE i2
(e1<s2)
– i1 MEETS i2
(s2 = e1)
– i1 EQUALS i2
(s1 = s2 AND e1 = e2)
– i1 OVERLAPS i2
(s2 < s1 < e2 OR s1 < s2 < e1)
i1
i1
i1
i1
i2
i2
i2
i2

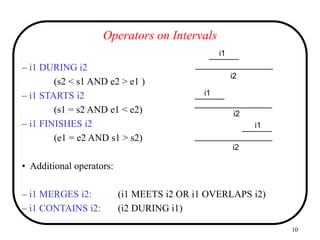
10
Operators on Intervals
– i1 DURING i2
(s2 < s1 AND e2 > e1 )
– i1 STARTS i2
(s1 = s2 AND e1 < e2)
– i1 FINISHES i2
(e1 = e2 AND s1 > s2)
• Additional operators:
– i1 MERGES i2: (i1 MEETS i2 OR i1 OVERLAPS i2)
– i1 CONTAINS i2: (i2 DURING i1)
i1
i2
i1
i1
i2
i2

11
Scalar and Relational Operators
• DURATION(i) - returns the number of time points in i
– eg. DURATION ([d03,d07]) returns 5
• i1 UNION i2
– returns [MIN(s1,s2),MAX(e1,e2) ]
if (i1 MERGES i2)
otherwise undefined
• i1 INTERSECT i2
– returns [MAX(s1,s2),MIN(e1,e2)]
if (i1 OVERLAPS i2)
otherwise undefined

12
Aggregate Operators
• EXPAND(X):
Where X is a set. The output is also a set.
Used to generate time quantum intervals.
– The expanded form of X is the set of all intervals of the form [p,p]
where p is a time point in some interval in X.
• e.g.:
– X1 = { [d01,d01],[d03,d05],[d04,d06] }
– X2 = { [d01,dp1],[d03,d04],[d05,d05],[d05,d06] }
– X3 = { [d01,d01],[d03,d03],[d04,d04],[d05,d05],[d06,d06] }
– Then EXPAND(X1) = EXPAND(X2) = X3

13
Aggregate Operators
• COLLAPSE(X):
The collapsed form of X is the set Y of intervals of the same type
such that
– (a) X & Y have the same unfolded form.
– (b) no two distinct members i1 and i2 of Y are such that (i1
MERGES i2) is true.
• e.g.:
– X1 = { [d01,d01],[d03,d05],[d04,d06] }
– X2 = { [d01,d01],[d03,d04],[d05,d05],[d05,d06] }
– X3 = { [d01,d01],[d03,d06] }
– Then COLLAPSE (X1) = COLLAPSE (X2) = X3

14
Relation Operators Involving
Intervals
• PACK r on A: groups the relation r by all its attributes apart from A
This is equivalent to
WITH ( r GROUP {A} AS X ) AS R1
( EXTEND R1 ADD COLLAPSE (X) AS Y )
{ALL BUT X } AS R2 :
R2 UNGROUP Y
• UNPACK r on A:
Replace COLLAPSE with EXPAND in PACK.

15
Example
S# P# During
S1 P1 [d04,d10]
S1 P7 [d05,d10]
S1 P3 [d09,d10]
S1 P5 [d06,d10]
S2 P1 [d02,d04]
S2 P9 [d03,d03]
S2 P1 [d08,d10]
S2 P5 [d09,d10]
S3 P1 [d08,d10]
S4 P2 [d06,d09]
S4 P5 [d04,d08]
S4 P7 [d05,d10]
SP
S# During
S1 [d04,d10]
S2 [d02,d04]
S2 [d07,d10]
S3 [d03,d10]
S4 [d04,d10]
S5 [d02,d10]
S
Given two temporal relations:
S: Supplier S# was under contract
during the interval During
SP: Supplier S# was able to supply
part P# during the interval During

16
Example 1
• Active supplier intervals: Get S#-DURING pairs for
suppliers who have been able to supply at least one
part during at least one interval of time, where
DURING designates such an interval.
• PACK SP {S#,DURING} ON DURING
S# P# During
S1 P1 [d04,d10]
S1 P7 [d05,d10]
S1 P3 [d09,d10]
S1 P5 [d06,d10]
S2 P1 [d02,d04]
S2 P9 [d03,d03]
S2 P1 [d08,d10]
S2 P5 [d09,d10]
S3 P1 [d08,d10]
S4 P2 [d06,d09]
S4 P5 [d04,d08]
S4 P7 [d05,d10]
SP
S# During
S1 [d04,d10]
S2 [d02,d04]
S2 [d08,d10]
S3 [d08,d10]
S4 [d04,d10]
RESULT

17
Example 2
• Inactive (passive) supplier intervals: Get S#-DURING pairs for
suppliers who have been unable to supply any parts at all during at
least one interval of time, where DURING designates such an
interval.
• PACK
( ( UNPACK S {S#,DURING} ON DURING )
MINUS
( UNPACK SP {S#,DURING} ON DURING ) )
ON DURING
• Shorthand: U_MINUS
S# During
S2 [d07,d07]
S3 [d03,d07]
S5 [d02,d10]
RESULT

18
More Relational Operators
• USING ( AList ) ◄ r1 op r2 ► is a shorthand for:
PACK
( ( UNPACK r1 on (AList) ) op ( UNPACK r1 on (AList) ) )
ON (AList)
Where op is either UNION, INTERSECT, MINUS or JOIN
• Various comparison operators on relations are defined similarly.
USING ( AList ) ◄ r1 rel-op r2 ► is equivalent to
( ( UNPACK r1 on (AList) ) rel-op ( UNPACK r1 on (AList) ) )

19
Part 2
Persistent B-trees
and applications

20
Persistent B-tree
• In some applications we are interested in being able to access
previous versions of data structure
– Databases
– Geometric data structures
• Partial persistence:
– Update the current version (getting a new version)
– Query all versions
• We would like to have partial persistent B-tree with
– O(N/B) space – N is number of updates performed
– update
– query in any version
)
(log B
T
B N
O 
)
(log N
O B

21
Persistent B-tree
• East way to make B-tree partial persistent
– Copy structure at each operation
– Maintain “version-access” structure (B-tree)
• Good query in any version, but
– O(N/B) I/O update
– O(N2/B) space
)
(log B
T
B N
O 
i i+2
i+1
update
i+3
i i+2
i+1

22
Persistent B-tree
• Idea: Elements augmented with “existence interval” and stored in
one structure
• Persistent B-tree with parameter b:
– Directed graph
* Nodes contain elements augmented with existence interval
* At any time t, nodes with elements alive at time t form B-tree
with leaf and branching parameter b (i.e., each node/leaf has
at least b/4 and at most b children/keys in them)
– B-tree with leaf and branching parameter b on indegree 0 nodes

If b=B: Query at any time t in I/Os
)
(log B
T
B N
O 

23
Persistent B-tree: Updates
• Updates performed as in B-tree
• To obtain linear space we maintain new-node invariant:
– New node contains between and alive elements and no
dead elements
B
8
3 B
8
7
B
4
1 B
8
7
B
8
3
B
B
8
1
B
8
1
B
2
1

24
B
4
1 B
8
7
B
8
3
B
Persistent B-tree Insert
• Search for relevant leaf u and insert new element
• If u contains B+1 elements: Block overflow
– Version split:
Mark u dead and create new node u’ with x alive element
– If : Strong overflow
– If : Strong underflow
– If then recursively update parent(u):
Delete (persistently) reference to u and insert reference to u’
B
4
1 B
8
7
B
8
3
B
B
x 8
7

B
x 8
3

B
x
B 8
7
8
3 


25
Persistent B-tree Insert
• Strong overflow ( )
– Split u into u’ and u’’ with elements each ( )
– Recursively update parent(u):
Delete reference to u and insert reference to v’ and v’’
• Strong underflow ( )
– Merge x elements with y live elements obtained by version split on
sibling ( )
– If then (strong overflow) perform split into nodes
with (x+y)/2 elements each ( )
– Recursively update parent(u): Delete two insert one/two references
B
4
1 B
8
7
B
8
3
B
B
4
1 B
8
7
B
8
3
B
B
4
1 B
8
7
B
8
3
B
2
x
B
4
1 B
8
7
B
8
3
B
B
B x
2
1
2
8
3 

B
x 8
7

B
y
x
B 8
11
2
1 


B
y
x 8
7


B
x 8
3

B
y
x
B 16
11
16
7 2
/
)
( 



26
Persistent B-tree Delete
• Search for relevant leaf u and mark element dead
• If u contains alive elements: Block underflow
– Version split:
Mark u dead and create new node u’ with x alive element
– Strong underflow ( ):
Merge (version split) and possibly split (strong overflow)
– Recursively update parent(u):
Delete two references insert one or two references
B
x 4
1

B
4
1 B
8
7
B
8
3
B
B
8
1
B
8
1
B
2
1
B
x 8
3


27
Persistent B-tree
B
4
1 B
8
7
B
8
3
B
B
8
1
B
8
1
B
2
1
Insert Delete
done
Block overflow Block underflow
done
Version split Version split
Strong overflow Strong underflow
Merge
Split
done
done
Strong overflow
Split
done
-1,+1
-1,+2
-2,+2
-2,+1
0,0

28
Persistent B-tree Analysis
• Update:
– Search and “rebalance” on one root-leaf path
• Space: O(N/B)
– At least updates in leaf in existence interval
– When leaf u dies
* At most two other nodes are created
* At most one block over/underflow one level up (in parent(u))

– During N updates we create:
* leaves
* nodes i levels up
 blocks
B
4
1 B
8
7
B
8
3
B
B
8
1
B
8
1
B
2
1
)
(log N
O B
B
8
1
)
(
)
( B
N
i
B
N O
O i 

)
( i
B
N
O
)
( B
N
O

29
Summary/Conclusion: Persistent B-tree
• Persistent B-tree
– Update current version
– Query all versions
• Efficient implementation obtained using existence intervals
– Standard technique

• During N operations
– O(N/B) space
– update
– query
)
(log B
T
B N
O 
)
(log N
O B

30
• Problem:
– Maintain N intervals with unique endpoints dynamically such
that stabbing query with point x can be answered efficiently
• As in (one-dimensional) B-tree case we are interested in
– space
– update
– query
Interval Management
)
(log B
T
B N
O 
)
(log N
O B
)
( B
N
O
x

31
Interval Management: Static Solution
• Sweep from left to right maintaining persistent B-tree
– Insert interval when left endpoint is reached
– Delete interval when right endpoint is reached
• Query x answered by reporting all intervals in B-tree at “time” x
– space
– query
– construction using buffer technique
• Dynamic with insert bound using logarithmic method
x
)
(log B
T
B N
O 
)
( B
N
O
)
(log2
N
O B
)
log
( N
O B
B
N

32
Internal Memory Logarithmic Method Idea
• Given (semi-dynamic) structure D on set V
– O(log N) query, O(log N) delete, O(N log N) construction
• Logarithmic method:
– Partition V into subsets V0, V1, … Vlog N, |Vi| = 2i or |Vi| = 0
– Build Di on Vi
* Delete: O(log N)
* Query: Query each Di  O(log2 N)
* Insert: Find first empty Di and construct Di out of
elements in V0,V1, … Vi-1
– O(2i log 2i) construction  O(log N) per moved element
– Element moved O(log N) times  amortized
..................................
0
2
2
2
2 1 2 log N
i
i
j
j
2
2
1 1
0 
 


)
(log2
N
O

33
i
i
j
j
B
B 
 


1
0
1
External Logarithmic Method Idea
)
(log2
N
O B ..................................
0
B
B
B
B 1 2 log N
B
  
i
j
i
j B
V
0





1
0
1
i
j
i
j B
V
)
(log2
N
O B
• Decrease number of subsets Vi
to logB N to get query
• Problem: Since there are not enough elements in
V0,V1, … Vi-1 to build Vi
• Solution: We allow Vi to contain any number of elements  Bi
– Insert: Find first Di such that and construct new
Di from elements in V0,V1, … Vi
* We move elements
* If Di constructed in O((|Vi|/B)logB |Vi|) = O(Bi-1logB N) I/Os
every moved element charged O(logB N) I/Os
* Element moved O(logB N) times  amortized

34
External Logarithmic Method Idea
• Given (semi-dynamic) linear space external data structure with
– I/O query
– I/O construction
(– I/O delete)

• Linear space dynamic data structure with
– I/O query
– I/O insert amortized
(– I/O delete)
• Dynamic interval management
– I/O query
– I/O insert amortized
)
(log B
T
B N
O 
)
log
( N
O B
B
N
)
(log N
O B
)
(log2
B
T
B N
O 
)
(log2
N
O B
)
(log N
O B
)
(log2
B
T
B N
O 
)
(log2
N
O B x

35
Planar Point Location
• Static problem:
– Store planar subdivision with N segments on disk such that
region containing query point q can be found I/O-efficiently
• We concentrate on vertical ray shooting query
– Segments can store regions it bounds
– Segments do not have to form subdivision
• Dynamic problem:
– Insert/delete segments
(we will not discuss this)
q

36
Static Solution
• Vertical line imposes above-below order on intersected segments
• Sweep from left to right maintaining
persistent B-tree on above-below order
– Left endpoint: Insert segment
– Right endpoint: Delete segment
• Query q answered by successor query on B-tree at time qx
– space
– query
)
(log B
T
B N
O 
)
( B
N
O
q

37
Static Solution
• Note: Not all segments comparable!
– Have to be careful about what we compare

• Problem: Routing elements in internal nodes of leaf oriented B-trees
– Luckily we can modify persistent B-tree to use regular (live)
elements as routing elements
• However, buffer technique construction cannot be used

• Only I/O construction algorithm
• Cannot be made dynamic using logarithmic method
q
)
log
( N
N
O B

38
References
• External Memory Geometric Data Structures
Lecture notes by Lars Arge.
– Section 1-4
• I/O-efficient Point Location using Persistent B-trees
– Lars Arge, Andrew Danner and Sha-Mayn Teh

Temporal PPT details about the platform and its uses

More Related Content

Similar to Temporal PPT details about the platform and its uses

Recently uploaded

Temporal PPT details about the platform and its uses