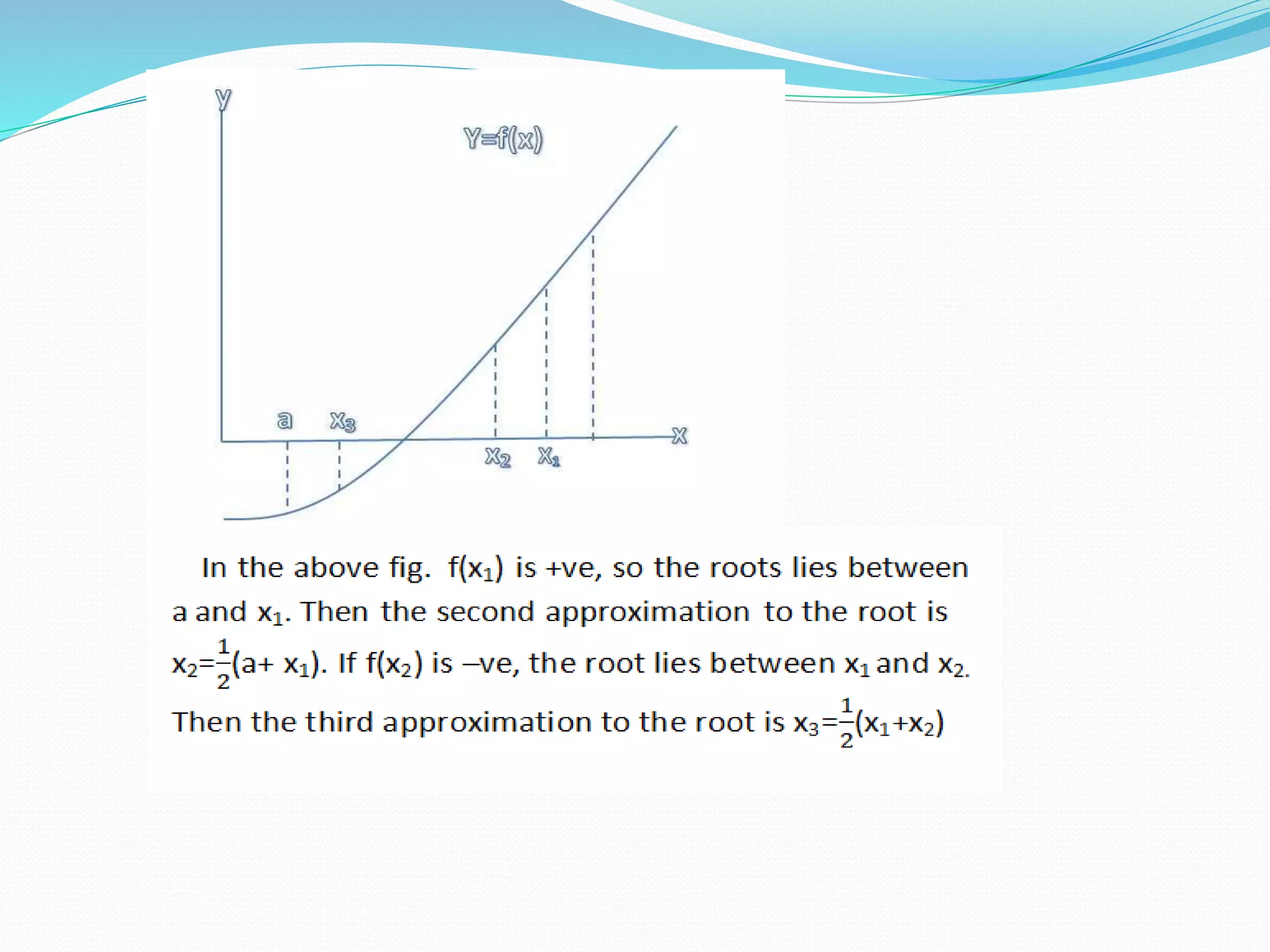
This document discusses numerical methods for solving algebraic and transcendental equations. It introduces the bisection method, regula-falsi method, and Newton-Raphson method. The bisection method locates the root of an equation between two values where the function values have opposite signs. It takes the midpoint of the interval and checks the function value there. If it has the same sign as the left value, the root must lie in the left interval, otherwise it is in the right interval. The process continues iteratively until the root is found to the desired accuracy.

1. NUMERICAL METHODS FOR THE SOLUTION OF
ALGEBRAIC AND TRANSCENDENTAL EQUATIONS

2. SOLUTION OF NON LINEAR
EQUATIONS
Numerical solution of Algebraic
and Transcendental Equations
 Introduction
 Bisection Method
 Regula-falsi Method
 Newton-Raphson Method

3. INTRODUCTION
 Numerical methods consist in repeated execution of same
process where at each step the result of preceding step is
used. So , basically it is known as iteration process and is
repeated till we get the desire degree of accuracy.
 In this chapter we shall discus some numerical methods for
the solution of algebraic and transcendental equations.

4. To find the root of f(x)= 0
Algebraic Equations Transcendental Equations
An algebraic Equation which
contain pure polynomial function
i.e. f(x) is a polynomial and
highest power of x should be finite
is called algebraic equation.
For example:
 x³-2x-5=0
 x³-6x+4=0
An Equation which contains
logarithmic functions, exponential
functions and trigonometric
functions is called transcendental
equation . In this equation highest
power of x is infinite.
For example:
 x-cosx=0
 2x-logx=6

5. METHODS TO FIND THE ROOT OF GIVEN EQUATION
 Bisection Method
 Regula-falsi Method
 Newton-Raphson Method

6. BISECTION METHOD
This method consist in locating the root of equation f(x)=0 between a
and b
If f(x) is continuous between a and b and f(a) and f(b) are of opposite
signs then, there is a root between a and b
Illustration:
Let f(a) is positive and f(b) is negative then, the first approximation to
the root is
If =0, then is the root of f(x)=0
If is negative then the root lies between a and
If is positive then the root lies between and b
Then we continue the previous process until the root is found to desire
accuracy

12. THANKS
BALJIT KAUR