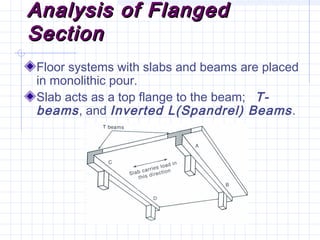
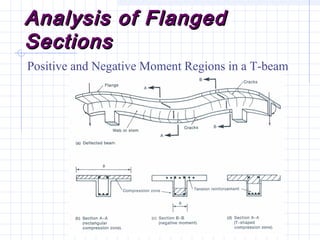
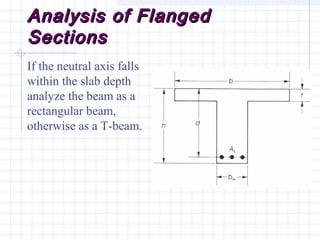
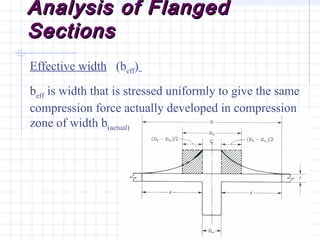
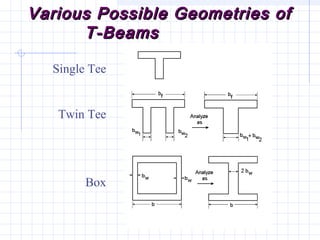
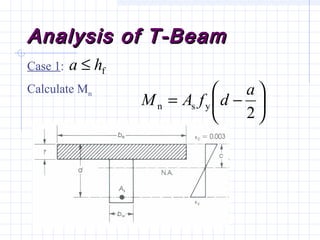
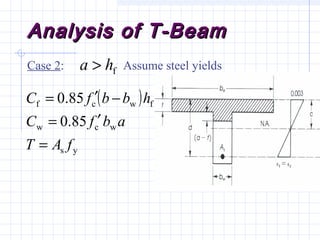
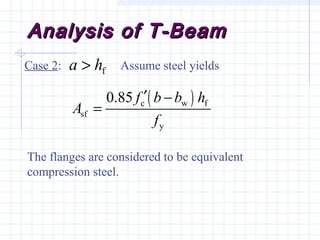
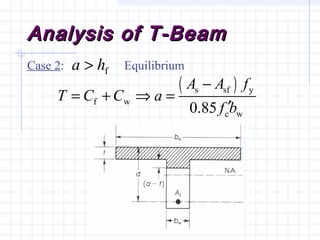
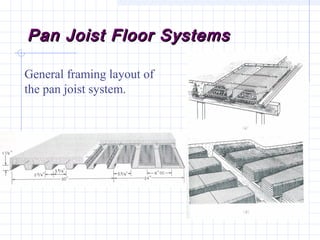
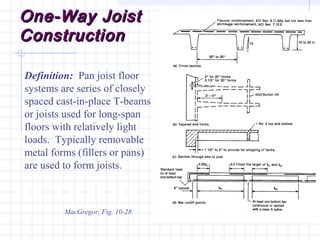
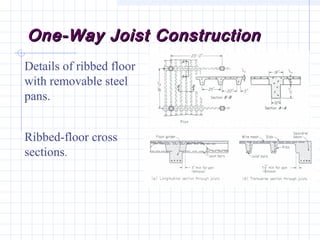
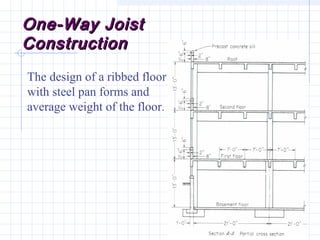
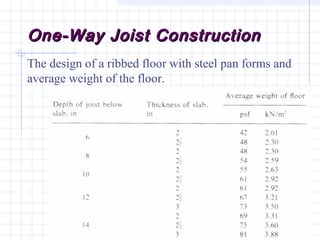
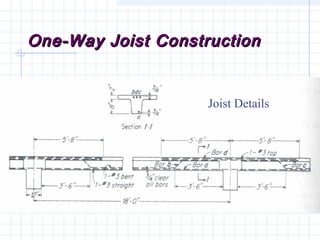
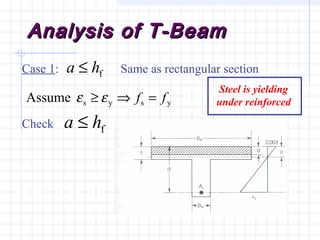
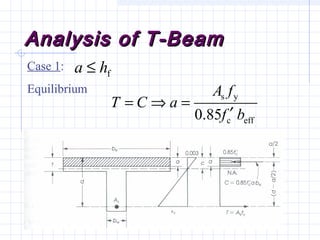
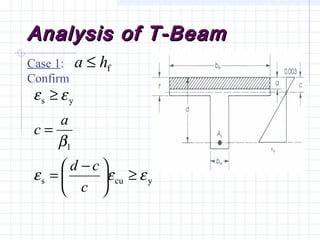
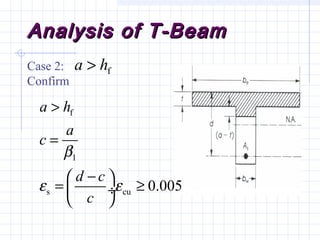
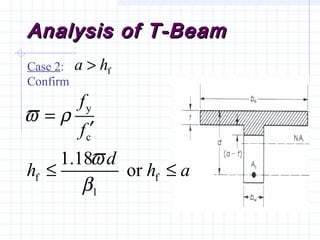
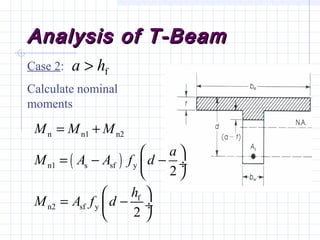
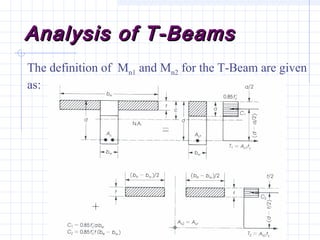
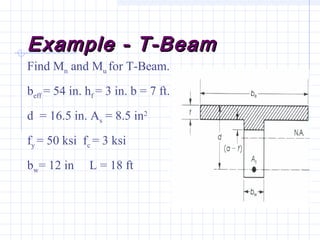
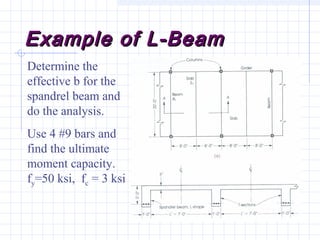
1) The document discusses the analysis of flanged beam sections like T-beams and L-beams. It covers topics like effective flange width, positive and negative moment regions, and ACI code provisions for estimating effective flange width. 2) Examples are provided for analyzing a T-beam and an L-beam section. This includes calculating the effective flange width, checking steel strain, minimum reinforcement requirements, and computing nominal moments. 3) Reinforcement limitations for flange beams are also outlined, covering requirements for flanges in compression and tension.

1. Lecture 7 - Flexure
June 16, 2003
CVEN 444

2. Lecture GoalsLecture Goals
Doubly Reinforced beams
T Beams and L Beams
Pan Joist

3. Analysis of FlangedAnalysis of Flanged
SectionSection
Floor systems with slabs and beams are placed
in monolithic pour.
Slab acts as a top flange to the beam; T-
beams, and Inverted L(Spandrel) Beams.

4. Analysis of FlangedAnalysis of Flanged
SectionsSections
Positive and Negative Moment Regions in a T-beam

5. Analysis of FlangedAnalysis of Flanged
SectionsSections
If the neutral axis falls
within the slab depth
analyze the beam as a
rectangular beam,
otherwise as a T-beam.

6. Analysis of FlangedAnalysis of Flanged
SectionsSections
Effective Flange Width
Portions near the webs are more highly stressed than
areas away from the web.

7. Analysis of FlangedAnalysis of Flanged
SectionsSections
Effective width (beff)
beff is width that is stressed uniformly to give the same
compression force actually developed in compression
zone of width b(actual)

8. ACI Code Provisions forACI Code Provisions for
Estimating bEstimating beffeff
From ACI 318, Section 8.10.2
T Beam Flange:
eff
f w
actual
4
16
L
b
h b
b
≤
≤ +
≤

9. ACI Code Provisions forACI Code Provisions for
Estimating bEstimating beffeff
From ACI 318, Section 8.10.3
Inverted L Shape Flange
( )
eff w
f w
actual w
12
6
0.5* clear distance to next web
L
b b
h b
b b
≤ +
≤ +
≤ = +

10. ACI Code Provisions forACI Code Provisions for
Estimating bEstimating beffeff
From ACI 318, Section 8.10
Isolated T-Beams
weff
w
f
4
2
bb
b
h
≤
≥

11. Various Possible Geometries ofVarious Possible Geometries of
T-BeamsT-Beams
Single Tee
Twin Tee
Box

12. Analysis of T-BeamAnalysis of T-Beam
Case 1: Same as rectangular section
Steel is yielding
under reinforced
Check fha ≤
fha ≤
ysysAssume ff =⇒≥ εε

13. Analysis of T-BeamAnalysis of T-Beam
Case 1:
Equilibrium
fha ≤
s y
c eff0.85
A f
T C a
f b
= ⇒ =
′

14. Analysis of T-BeamAnalysis of T-Beam
Case 1:
Confirm
fha ≤
ycus
1
ys
εεε
β
εε
≥




 −
=
=
≥
c
cd
a
c

15. Analysis of T-BeamAnalysis of T-Beam
Case 1:
Calculate Mn
fha ≤






−=
2
ysn
a
dfAM

16. Analysis of T-BeamAnalysis of T-Beam
Case 2: Assume steel yieldsfha >
( )
ys
wcw
fwcf
85.0
85.0
fAT
abfC
hbbfC
=
′=
−′=

17. Analysis of T-BeamAnalysis of T-Beam
Case 2: Assume steel yieldsfha >
( )c w f
sf
y
0.85 f b b h
A
f
′ −
=
The flanges are considered to be equivalent
compression steel.

18. Analysis of T-BeamAnalysis of T-Beam
Case 2: Equilibriumfha >
( )s sf y
f w
c w0.85
A A f
T C C a
f b
−
= + ⇒ =
′

19. Analysis of T-BeamAnalysis of T-Beam
Case 2:
Confirm
fha >
f
1
s cu 0.005
a h
a
c
d c
c
β
ε ε
>
=
− 
= ≥ ÷
 

20. Analysis of T-BeamAnalysis of T-Beam
Case 2:
Confirm
fha >
y
c
f f
1
1.18
or
f
f
d
h h a
ϖ ρ
ϖ
β
=
′
≤ ≤

21. Analysis of T-BeamAnalysis of T-Beam
Case 2:
Calculate nominal
moments
fha >
( )
n n1 n2
n1 s sf y
f
n2 sf y
2
2
M M M
a
M A A f d
h
M A f d
= +
 
= − − ÷
 
 
= − ÷
 

22. Analysis of T-BeamsAnalysis of T-Beams
The definition of Mn1 and Mn2 for the T-Beam are given
as:

23. Analysis of T-BeamsAnalysis of T-Beams
The ultimate moment Mu for the T-Beam are given as:
u nM M
c
f
d
φ
φ
=
 
=  ÷
 
For a T-Beam with the
tension steel yielded using a
function c/d

24. Limitations on ReinforcementLimitations on Reinforcement
for Flange Beamsfor Flange Beams
Lower Limits
 Flange in compression
c
ys
min
w
y
3
larger of
200
f
fA
b d
f
ρ
 ′


= = 




25. Limitations on ReinforcementLimitations on Reinforcement
for Flange Beamsfor Flange Beams
Lower Limits
 Flange in tension
















 ′
′
=
db
f
db
f
f
db
f
f
A
eff
y
eff
y
c
w
y
c
s(min)
200
3
oflarger
6
ofsmaller

26. Limitations on ReinforcementLimitations on Reinforcement
for Flange Beamsfor Flange Beams
Lower Limits
 If As(provided) 4/3 As(req’d) based on analysis
then As(min) is not required (i.e.)
φMn
4/3Mu for As(provided)
See ACI 10.5.3
≥
≥

27. Example - T-BeamExample - T-Beam
Find Mn and Mu for T-Beam.
beff = 54 in. hf = 3 in. b = 7 ft.
d = 16.5 in. As = 8.5 in2
fy = 50 ksi fc = 3 ksi
bw= 12 in L = 18 ft

28. Example of L-BeamExample of L-Beam
Confirm beff
( )
eff
f w
12 in.
18 ft
ft.
54 in.
4 4
16 16 3 in. 12 in.=60 in.
12 in.
7 ft. 84 in.
ft.
L
b
h b
b
 
 ÷
 ≤ = =
≤ + = +
 
≤ = = ÷
 

29. Example - T-BeamExample - T-Beam
( )( )
( ) ( )
2
s y
c eff
1
s
8.5 in 50 ksi
3.09 in.
0.85 0.85 3 ksi 54 in.
3.09 in
3.63 in.
0.85
16.5 in.
1 0.003 1 0.003 0.0106 0.005
3.63 in.
A f
a
f b
a
c
d
c
β
ε
= = =
′
= = =
   
= − = − = >   
   
Compute the equivalent c value and check the strain
in the steel, εs
Steel will yield in the tension zone.

30. Example - T-BeamExample - T-Beam
( )
( ) ( )
2
s
w
y
min min
c
y
8.5 in
0.0429
12 in. 16.5 in.
200 200
0.004
50000
0.004
3 3 3000
0.00329
50000
0.0429 0.004
A
b d
f
f
f
ρ
ρ ρ
= = =

= =

= ⇒ =
 = =


>
Compute the reinforcement ρ and check to make sure it
is greater than ρmin
Section works for minimum
reinforcement.

31. Example - T-BeamExample - T-Beam
( ) ( )
y
c
f
1
f
50 ksi
0.0429 0.7155
3 ksi
1.18 0.7155 16.5 in.1.18
3 in. 16.388
0.85
3 in. 3.09 in.
f
f
d
h
h a
ϖ ρ
ϖ
β
 
= = = ÷′  
≤ ⇒ ≤ =
≤ ⇒ ≤
Compute ω and check that the c value is greater than hf
Analysis the beam as a T-beam.

32. Example - T-BeamExample - T-Beam
Compute ω and check that the c value is greater than hf
Compute a
( ) ( ) ( ) ( )
( )
c eff w f
sf
y
2
0.85 0.85 3 ksi 54 in. 12 in. 3 in.
50 ksi
6.426 in
f b b h
A
f
′ − −
= =
=
( ) ( )( )
( ) ( )
2 2
s sf y
c w
8.5 in 6.426 in 50 ksi
0.85 0.85 3 ksi 12 in.
3.889 in.
A A f
a
f b
−−
= =
′
=

33. Example - T-BeamExample - T-Beam
Compute nominal moment components
( )( )2f
n2 sf y
3 in.
6.426 in 50 ksi 16.5 in.
2 2
4819.5 k-in.
h
M A f d
   
= − = −   
   
=
( )
( )( )
n1 s sf y
2 2
2
3.889 in.
8.5 in 6.426 in 50 ksi 16.5 in.
2
1535.34 k-in.
a
M A A f d
 
= − − 
 
 
= − − 
 
=

34. Example - T-BeamExample - T-Beam
Compute nominal moment
( )u n 0.9 529.57 k-ft.
416.6 k-ft.
M Mφ= =
=
n n1 n2
1535.34 k-in. 4819.5 k-in.
6354.84 k-in. 529.57 k-ft.
M M M= +
= +
= ⇒
Compute ultimate moment

35. Example of L-BeamExample of L-Beam
Determine the
effective b for the
spandrel beam and
do the analysis.
Use 4 #9 bars and
find the ultimate
moment capacity.
fy=50 ksi, fc = 3 ksi

36. Example of L-BeamExample of L-Beam
Compute beff
( )
eff w
f w
actual w
12
6
0.5* clear distance to next web
L
b b
h b
b b
≤ +
≤ +
≤ = +

37. Example of L-BeamExample of L-Beam
Compute beff
( )
( )
eff w
f w
actual w
12 in.
20 ft
ft
12 in. =32 in.
12 12
6 6 6 in. 12 in. = 48 in.
0.5* clear distance to next web
12 in.
12 in. + 0.5* 7 ft 54 i
ft
L
b b
h b
b b
 
 ÷
 ≤ + = +
≤ + = +
≤ = +
  
= = ÷ ÷
  
n.

38. Example of L-BeamExample of L-Beam
The value beff and As
( )
eff
2 2
s
= 32 in.
4 1.0 in 4.0 in
b
A = =

39. Example - L-BeamExample - L-Beam
( )( )
( ) ( )
2
s y
c eff
1
s
4.0 in 50 ksi
2.45 in.
0.85 0.85 3 ksi 32 in.
2.45 in
2.88 in.
0.85
24 in.
1 0.003 1 0.003 0.0220 0.005
2.88 in.
A f
a
f b
a
c
d
c
β
ε
= = =
′
= = =
   
= − = − = > ÷  ÷
   
Compute the equivalent c value and check the strain
in the steel, εs
Steel will yield in the tension zone.

40. Example - L-BeamExample - L-Beam
( )
( ) ( )
2
s
w
y
min min
c
y
4.0 in
0.0139
12 in. 24 in.
200 200
0.004
50000
0.004
3 3 3000
0.00329
50000
0.0139 0.004
A
b d
f
f
f
ρ
ρ ρ
= = =

= =

= ⇒ =
 = =


>
Compute the reinforcement ρ and check to make sure it
is greater than ρmin
Section works for minimum
reinforcement.

41. Example - L-BeamExample - L-Beam
( ) ( )
y
c
f
1
f
50 ksi
0.0139 0.2315
3 ksi
1.18 0.2315 24 in.1.18
6 in. 7.71 in.
0.85
6 in. 2.45 in.
f
f
d
h
h a
ϖ ρ
ϖ
β
 
= = = ÷′  
≤ ⇒ ≤ =
≤ ⇒ ≤
Compute ω and check that the c value is greater than hf
Analysis the beam as a Singly reinforced beam.
False!

42. Example - L-BeamExample - L-Beam
Compute a
( )( )
( ) ( )
2
s y
c
4.0 in 50 ksi
0.85 0.85 3 ksi 32 in.
2.451 in.
A f
a
f b
= =
′
=

43. Example - L-BeamExample - L-Beam
Compute nominal moment
( )( )
n s y
2
2
2.451 in.
4.0 in 50 ksi 24.0 in.
2
4554.9 k-in. 379.58 k-ft.
a
M A f d
 
= − ÷
 
 
= − ÷
 
= ⇒

44. Example - L-BeamExample - L-Beam
( )u n 0.9 379.58 k-ft.
341.62 k-ft.
M Mφ= =
=
Compute ultimate moment

45. Pan Joist Floor SystemsPan Joist Floor Systems
View of Pan Joist Slab from Below Walter P. Moore & Assoc.

46. Pan Joist Floor SystemsPan Joist Floor Systems
View of Double Skip Joist Slab from Below
Walter P. Moore & Assoc.

47. Pan Joist FloorPan Joist Floor
SystemsSystems
Placing Reinforcement
for a Pan Joist Slab
Walter P. Moore & Assoc.

48. Pan Joist Floor SystemsPan Joist Floor Systems
General framing layout of
the pan joist system.

49. Pan Joist FloorPan Joist Floor
SystemsSystems
Pouring a Pan Joist Slab
Walter P. Moore & Assoc.

50. Pan Joist Floor SystemsPan Joist Floor Systems
Definition: The type of slab is also called a
ribbed slab. It consists of a floor slab, usually
2-4 in. thick, supported by reinforced concrete
ribs. The ribs are usually tapered and
uniformly spaced at distances that do not
exceed 30 in. The ribs are supported on
girders that rest on columns. In some ribbed
slabs, the space between ribs may be filled
with permanent fillers to provide a horizontal
slab soffit.

51. One-Way JoistOne-Way Joist
ConstructionConstruction
MacGregor, Fig. 10-28
Definition: Pan joist floor
systems are series of closely
spaced cast-in-place T-beams
or joists used for long-span
floors with relatively light
loads. Typically removable
metal forms (fillers or pans)
are used to form joists.

52. One-Way Joist ConstructionOne-Way Joist Construction
Details of ribbed floor
with removable steel
pans.
Ribbed-floor cross
sections.

53. One-Way JoistOne-Way Joist
ConstructionConstruction
The design of a ribbed floor
with steel pan forms and
average weight of the floor.

54. One-Way Joist ConstructionOne-Way Joist Construction
The design of a ribbed floor with steel pan forms and
average weight of the floor.

55. One-Way Joist ConstructionOne-Way Joist Construction
Joist Details

56. Pan Joist Floor SystemsPan Joist Floor Systems
ACI Requirements for Joist Construction
(Sec. 8.11, ACI 318-02)
 Slabs and ribs must be cast monolithically.
 Ribs must be spaced consistently
 Ribs may not be less than 4 inches in width

57. Pan Joist Floor SystemsPan Joist Floor Systems
ACI Requirements for Joist Construction (cont.)
(Sec. 8.11.2, ACI 318-02)
 Depth of ribs may not be more than 3.5 times
the minimum rib width
 Clear spacing between ribs shall not exceed
30 inches.
** Ribbed slabs not meeting these
requirements are designed as slabs and
beams. **

58. Pan Joist Floor SystemsPan Joist Floor Systems
Slab Thickness
 (ACI Sec. 8.11.6.1)
t 2 in. for joints formed with 20 in. wide pans
t 2.5 in. for joints formed with 30 in. wide
pans (1/12 distance)≥
≥

59. Pan Joist Floor SystemsPan Joist Floor Systems
Slab Thickness (cont.)
 Building codes give minimum fire resistance
rating:
1-hour fire rating: ¾ in. cover, 3”-3.5” slab
thickness
2-hour fire rating: 1 in. cover, 4.5” slab
thickness

60. FloorFloor
SystemsSystems
Standard
Removable Form
Dimensions
 Note the shapes

61. Pan Joist Floor SystemsPan Joist Floor Systems
Standard Removable Form Dimensions
 Standard Widths: 20 in. & 30 in.
(measured at bottom of ribs)
 Standard Depths: 6, 8, 10, 12, 14, 16 or
20 in.

62. Pan Joist Floor SystemsPan Joist Floor Systems
Standard Removable Form Dimensions
(cont.)
 End Forms: one end is closed (built-in) to
form the supporting beam
 Tapered End Forms: provide additional
shear capacity at ends of joists by tapering
ends to increase rib width.

63. Pan Joist
Slabs
Standard Pan Joist
Form Dimensions
Ref. CECO Concrete
Construction Catalog

64. Pan Joist
Slabs
Standard Pan Joist
Form Dimensions
Ref. CECO Concrete Construction
Catalog

65. Pan Joist Floor SystemsPan Joist Floor Systems
Laying Out Pan Joist Floors
 Rib/slab thickness
Governed by strength, fire rating,
available space
 Overall depth and rib thickness
Governed by deflections and shear

66. Pan Joist Floor SystemsPan Joist Floor Systems
Laying Out Pan Joist Floors (cont.)
 Typically no stirrups are used in joists
 Reducing Forming Costs:
Use constant joist depth for entire floor
Use same depth for joists and beams
(not always possible)

67. Pan Joist Floor SystemsPan Joist Floor Systems
Distribution Ribs
 Placed perpendicular to joists*
 Spans < 20 ft.: None
 Spans 20-30 ft.: Provided a midspan
 Spans > 30 ft.: Provided at third-points
 At least one continuous #4 bar is provided at top
and bottom of distribution rib.
*Note: not required by ACI Code, but typically used
in construction

68. Member DepthMember Depth
ACI provides minimum member depth and
slab thickness requirements that can be used
without a deflection calculation (Sec. 9.5 ACI
318)
 Useful for selecting preliminary member
sizes

69. Member DepthMember Depth
ACI 318 - Table 9.5a:
 Min. thickness, h (for beams or ribbed one-way
slab)
For beams with one end continuous: L/18.5
For beams with both ends continuous: L/21
L is span length in inches
 Table 9.5a usually gives a depth too shallow for
design, but should be checked as a minimum.

70. MemberMember
DepthDepth
ACI 318-99: Table 9.5a

71. Member DepthMember Depth
Rule of Thumb:
 hb (in.) ~ L (ft.)
 Ex.) 30 ft. span -> hb ~ 30 in.
 May be a little large, but okay as a start to
calc. DL
Another Rule of Thumb:
 wDL (web below slab) ~ 15% (wSDL+ wLL)
Note: For design, start with maximum
moment for beam to finalize depth.
Select b as a function of d
 b ~ (0.45 to 0.65) (d)