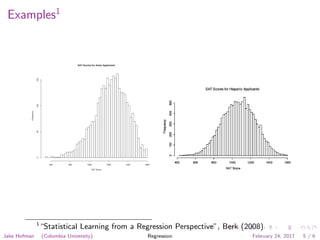
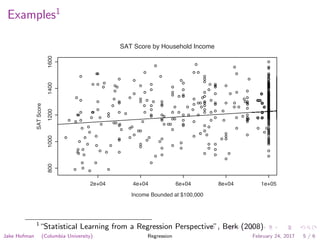
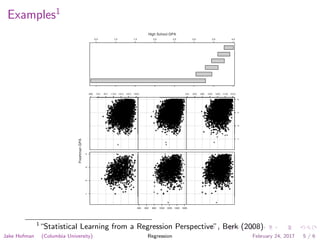
This document discusses regression analysis as presented by Jake Hofman of Columbia University. It defines regression as understanding how a response variable varies across subgroups based on predictor variables. The goals of regression are to describe outcomes under different conditions, predict future outcomes, and explain associations between predictors and outcomes. Examples shown include comparing SAT score distributions between ethnic groups and examining the relationship between SAT scores and household income. The framework for regression involves specifying the outcome and predictors, defining a loss function, fitting the model to minimize loss, and assessing performance.

1. Regression
APAM E4990
Modeling Social Data
Jake Hofman
Columbia University
February 24, 2017
Jake Hofman (Columbia University) Regression February 24, 2017 1 / 6

2. Definition
?
Jake Hofman (Columbia University) Regression February 24, 2017 2 / 6

3. Definition
Jake Hofman (Columbia University) Regression February 24, 2017 2 / 6

4. Definition
“The primary goal in a regression analysis is to
understand, as far as possible with the available data,
how the conditional distribution of the response varies
across subpopulations determined by the possible
values of the predictor or predictors.”
-“Applied Regression Including Computing and Graphics”
Cook & Weisberg (1999)
Jake Hofman (Columbia University) Regression February 24, 2017 2 / 6

5. Goals
Describe
Provide a compact summary of outcomes under different conditions
Predict
Make forecasts for future outcomes or unobserved conditions
Explain
Account for associations between predictors and outcomes
Jake Hofman (Columbia University) Regression February 24, 2017 3 / 6

6. Goals
Describe
Provide a compact summary of outcomes under different conditions
Never “false”, but may be wasteful or misleading
Predict
Make forecasts for future outcomes or unobserved conditions
Varying degrees of success, often room for improvement
Explain
Account for associations between predictors and outcomes
Difficult to establish causality in observational studies
See “Regression Analysis: A Constructive Critique”, Berk (2004)
Jake Hofman (Columbia University) Regression February 24, 2017 3 / 6

7. Goals
Models should be flexible enough to describe observed phenomena
but simple enough to generalize to future observations
Jake Hofman (Columbia University) Regression February 24, 2017 4 / 6

8. Examples1
1.2 Setting the Regression Context 3
Should one be especially interested in a comparison of the means, one could
roceed descriptively with a conventional least squares regression analysis as
special case. That is, for each observation i, one could let
ˆyi = β0 + β1xi, (1.1)
here the response variable y is each applicant’s SAT score, x is an indicator
Fig. 1.2. Distribution of SAT scores for Asian applicants.
SAT Scores for Asian Applicants
SAT Score
Frequency
600 800 1000 1200 1400 1600
050100150
of some response y varies across subpopulations determined by the po
values of the predictor or predictors” (Cook and Weisberg, 1999: 27).
is, interest centers on the distribution of the response variable Y conditi
on one or more predictors X.
This definition includes a wide variety of elementary procedures e
implemented in R. (See, for example, Maindonald and Braun, 2007: Ch
2.) For example, consider Figures 1.1 and 1.2. The first shows the distrib
of SAT scores for recent applicants to a major university, who self-ide
as “Hispanic.” The second shows the distribution of SAT scores for r
applicants to that same university, who self-identify as “Asian.”
Fig. 1.1. Distribution of SAT scores for Hispanic applicants.
It is clear that the two distributions differ substantially. The Asian
tribution is shifted to the right, leading to a distribution with a higher
(1227 compared to 1072), a smaller standard deviation (170 compared to
and greater skewing. A comparative description of the two histograms
constitutes a proper regression analysis. Using various summary stati
some key features of the two displays are compared and contrasted (
1
“Statistical Learning from a Regression Perspective”, Berk (2008)
Jake Hofman (Columbia University) Regression February 24, 2017 5 / 6

9. Examples1
aph more legible.
2e+04 4e+04 6e+04 8e+04 1e+05
8001000120014001600
SAT Score by Household Income
Income Bounded at $100,000
SATScore
Fig. 1.4. SAT scores by family income.1
“Statistical Learning from a Regression Perspective”, Berk (2008)
Jake Hofman (Columbia University) Regression February 24, 2017 5 / 6

10. Examples1
6 1 Regression Framework
1234
400 600 800 1000 1200 1400 1600
400 600 800 1000 1200 1400 1600 400 600 800 1000 1200 1400 1600
1234
FreshmanGPA
0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
High School GPA
Fig. 1.5. Freshman GPA on SAT holding high school GPA constant.1
“Statistical Learning from a Regression Perspective”, Berk (2008)
Jake Hofman (Columbia University) Regression February 24, 2017 5 / 6

11. Framework
• Specify the outcome and predictors, along with the form of
the model relating them
• Define a loss function that quantifies how close a model’s
predictions are to observed outcomes
• Develop an algorithm to fit the model to the observations by
minimizing this loss
• Assess model performance and interpret results.
Jake Hofman (Columbia University) Regression February 24, 2017 6 / 6