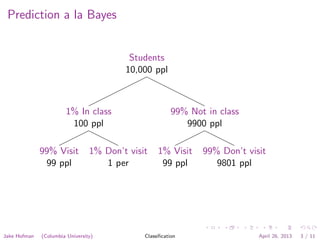
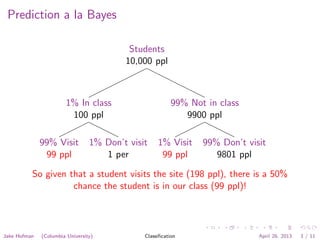
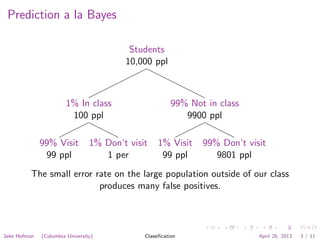
The document discusses the Naive Bayes classification algorithm. It explains how Naive Bayes can be used to classify students based on whether they visit an online course site. It describes representing each student as a binary vector indicating which sites they visited. The algorithm then treats site visits as independent Bernoulli trials to calculate the probability that a student is in a particular class based on the sites they visited. The document outlines how to estimate the model parameters from training data and use the model to make predictions.

1. Classification
APAM E4990
Computational Social Science
Jake Hofman
Columbia University
April 26, 2013
Jake Hofman (Columbia University) Classification April 26, 2013 1 / 11

2. Prediction a la Bayes1
• You’re testing for a rare condition:
• 1% of the student population is in this class
• You have a highly sensitive and specific test:
• 99% of students in the class visit compsocialscience.org
• 99% of students who aren’t in the class don’t visit this site
• Given that a student visits the course site, what is probability
the student is in our class?
1
Follows Wiggins, SciAm 2006
Jake Hofman (Columbia University) Classification April 26, 2013 2 / 11

3. Prediction a la Bayes
Students
10,000 ppl
1% In class
100 ppl
99% Visit
99 ppl
1% Don’t visit
1 per
99% Not in class
9900 ppl
1% Visit
99 ppl
99% Don’t visit
9801 ppl
Jake Hofman (Columbia University) Classification April 26, 2013 3 / 11

4. Prediction a la Bayes
Students
10,000 ppl
1% In class
100 ppl
99% Visit
99 ppl
1% Don’t visit
1 per
99% Not in class
9900 ppl
1% Visit
99 ppl
99% Don’t visit
9801 ppl
So given that a student visits the site (198 ppl), there is a 50%
chance the student is in our class (99 ppl)!
Jake Hofman (Columbia University) Classification April 26, 2013 3 / 11

5. Prediction a la Bayes
Students
10,000 ppl
1% In class
100 ppl
99% Visit
99 ppl
1% Don’t visit
1 per
99% Not in class
9900 ppl
1% Visit
99 ppl
99% Don’t visit
9801 ppl
The small error rate on the large population outside of our class
produces many false positives.
Jake Hofman (Columbia University) Classification April 26, 2013 3 / 11

6. Inverting conditional probabilities
Bayes’ Theorem
Equate the far right- and left-hand sides of product rule
p (y|x) p (x) = p (x, y) = p (x|y) p (y)
and divide to get the probability of y given x from the probability
of x given y:
p (y|x) =
p (x|y) p (y)
p (x)
where p (x) = y∈ΩY
p (x|y) p (y) is the normalization constant.
Jake Hofman (Columbia University) Classification April 26, 2013 4 / 11

7. Predictions a la Bayes
Given that a patient tests positive, what is probability the patient
is sick?
p (class|visit) =
99/100
p (visit|class)
1/100
p (class)
p (visit)
99/1002+99/1002=198/1002
=
99
198
=
1
2
where p (visit) = p (visit|class) p (class) + p visit|class p class .
Jake Hofman (Columbia University) Classification April 26, 2013 5 / 11

8. (Super) Naive Bayes
We can use Bayes’ rule to build a one-site student classifier:
p (class|site) =
p (site|class) p (class)
p (site)
where we estimate these probabilities with ratios of counts:
ˆp(site|class) =
# students in class who visit site
# students in class
ˆp(site|class) =
# students not in class who visit site
# students not in class
ˆp(class) =
# students in class
# students
ˆp(class) =
# students not in class
# students
Jake Hofman (Columbia University) Classification April 26, 2013 6 / 11

9. Naive Bayes
Represent each student by a binary vector x where xj = 1 if the
student has visited the j-th site (xj = 0 otherwise).
Modeling each site as an independent Bernoulli random variable,
the probability of visiting a set of sites x given class membership
c = 0, 1:
p (x|c) =
j
θ
xj
jc (1 − θjc)1−xj
where θjc denotes the probability that the j-th site is visited by a
student with class membership c.
Jake Hofman (Columbia University) Classification April 26, 2013 7 / 11

10. Naive Bayes
Using this likelihood in Bayes’ rule and taking a logarithm, we have:
log p (c|x) = log
p (x|c) p (c)
p (x)
=
j
xj log
θjc
1 − θjc
+
j
log(1 − θjc) + log
θc
p (x)
Jake Hofman (Columbia University) Classification April 26, 2013 8 / 11

11. Naive Bayes
We can eliminate p (x) by calculating the log-odds:
log
p (1|x)
p (0|x)
=
j
xj log
θj1(1 − θj0)
θj0(1 − θj1)
wj
+
j
log
1 − θj1
1 − θj0
+ log
θ1
θ0
w0
which gives a linear classifier of the form w · x + w0
Jake Hofman (Columbia University) Classification April 26, 2013 9 / 11

12. Naive Bayes
We train by counting students and sites to estimate θjc and θc:
ˆθjc =
njc
nc
ˆθc =
nc
n
and use these to calculate the weights ˆwj and bias ˆw0:
ˆwj = log
ˆθj1(1 − ˆθj0)
ˆθj0(1 − ˆθj1)
ˆw0 =
j
log
1 − ˆθj1
1 − ˆθj0
+ log
ˆθ1
ˆθ0
.
We we predict by simply adding the weights of the sites that a
student has visited to the bias term.
Jake Hofman (Columbia University) Classification April 26, 2013 10 / 11

13. Naive Bayes
In practice, this works better than one might expect given its
simplicity2
2
http://www.jstor.org/pss/1403452
Jake Hofman (Columbia University) Classification April 26, 2013 11 / 11

14. Naive Bayes
Training is computationally cheap and scalable, and the model is
easy to update given new observations2
2
http://www.springerlink.com/content/wu3g458834583125/
Jake Hofman (Columbia University) Classification April 26, 2013 11 / 11

15. Naive Bayes
Performance varies with document representations and
corresponding likelihood models2
2
http://ceas.cc/2006/15.pdf
Jake Hofman (Columbia University) Classification April 26, 2013 11 / 11

16. Naive Bayes
It’s often important to smooth parameter estimates (e.g., by
adding pseudocounts) to avoid overfitting
Jake Hofman (Columbia University) Classification April 26, 2013 11 / 11