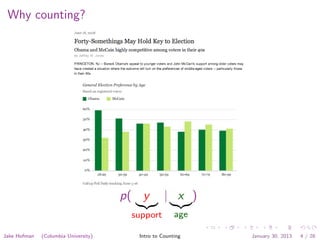
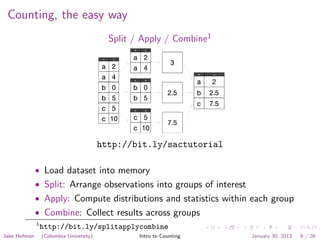
This document introduces counting and grouping large datasets. It discusses how to compute statistics on data when the full dataset exceeds memory capacity. It presents three approaches to grouping data: loading the full dataset into memory, streaming to process one observation at a time, and storing per-group histograms. The approaches vary in the types of statistics that can be computed based on the number of observations, groups, and distinct values within each group.
Siva Kumar Cheekula, Pavan Kapanipathi, Derek Doran, Amit P. Sheth. Entity Recommendations Using Hierarchical Knowledge Bases. In proceedings of 4th Workshop on Knowledge Discovery and Data Mining Meets Linked Open Data at ESWC2015, Slovenia, May 31, 2015.
Paper at the 4th Know@LOD 2015.
[RIIT 2017] Identifying Grey Sheep Users By The Distribution of User Similari...YONG ZHENG
Yong Zheng, Mayur Agnani, Mili Singh. “Identifying Grey Sheep Users By The Distribution of User Similarities In Collaborative Filtering”. Proceedings of The 6th ACM Conference on Research in Information Technology (RIIT), Rochester, NY, USA, October, 2017
Siva Kumar Cheekula, Pavan Kapanipathi, Derek Doran, Amit P. Sheth. Entity Recommendations Using Hierarchical Knowledge Bases. In proceedings of 4th Workshop on Knowledge Discovery and Data Mining Meets Linked Open Data at ESWC2015, Slovenia, May 31, 2015.
Paper at the 4th Know@LOD 2015.
[RIIT 2017] Identifying Grey Sheep Users By The Distribution of User Similari...YONG ZHENG
Yong Zheng, Mayur Agnani, Mili Singh. “Identifying Grey Sheep Users By The Distribution of User Similarities In Collaborative Filtering”. Proceedings of The 6th ACM Conference on Research in Information Technology (RIIT), Rochester, NY, USA, October, 2017
Building a Successful Facebook Marketing ProgramInternet Gal
As a marketer or small business owner, you put a lot of resources into engaging and interacting with your Facebook fans, but are you getting a positive return on your investment? How can you ensure the time (and money) you are devoting to the world\'s largest social network is well spent?
When it comes to Facebook, it takes a well formulated plan to create measurable and meaningful results.
Here is a presentation I recently have to the a Midwest security user group on how to manage multiple environments, or clients, with Symantec Endpoint Protection.
Building a Successful Facebook Marketing ProgramInternet Gal
As a marketer or small business owner, you put a lot of resources into engaging and interacting with your Facebook fans, but are you getting a positive return on your investment? How can you ensure the time (and money) you are devoting to the world\'s largest social network is well spent?
When it comes to Facebook, it takes a well formulated plan to create measurable and meaningful results.
Here is a presentation I recently have to the a Midwest security user group on how to manage multiple environments, or clients, with Symantec Endpoint Protection.
These slides refer to the talk I gave at the last ASE/IEEE SocialCom 2013 International Conference, where I presented the research work entitled "Trending Topics on Twitter Improve the Prediction of Google Hot Queries", which turned to be selected among the top-5% best accepted papers.
Once every five minutes, Twitter publishes a list of trending topics by monitoring and analyzing tweets from its users. Similarly, Google makes available hourly a list of hot queries that have been issued to the search engine. In this work, we analyze the time series derived from the daily volume index of each trend, either by Twitter or Google. Our study on a real-world dataset reveals that about 26% of the trending topics raising from Twitter "as-is" are also found as hot queries issued to Google. Also, we find that about 72% of the similar trends appear first on Twitter. Thus, we assess the relation between comparable Twitter and Google trends by testing three classes of time series regression models. We validate the forecasting power of Twitter by showing that models, which use Google as the dependent variable and Twitter as the explanatory variable, retain as significant the past values of Twitter 60% of times.
The presentation talks about raw scores and Measures of Central Tendency such as Mean, Median and Mode - its concept, methods of calculation and usages.
Clustering plays an important role in data mining as many applications use it as a preprocessing step for data analysis. Traditional clustering focuses on the grouping of similar objects, while two-way co-clustering can group dyadic data (objects as well as their attributes) simultaneously. Most co-clustering research focuses on single correlation data, but there might be other possible descriptions of dyadic data that could improve co-clustering performance. In this research, we extend ITCC (Information Theoretic Co-Clustering) to the problem of co-clustering with augmented matrix. We proposed CCAM (Co-Clustering with Augmented Data Matrix) to include this augmented data for better co-clustering. We apply CCAM in the analysis of on-line advertising, where both ads and users must be clustered. The key data that connect ads and users are the user-ad link matrix, which identifies the ads that each user has linked; both ads and users also have their feature data, i.e. the augmented data matrix. To evaluate the proposed method, we use two measures: classification accuracy and K-L divergence. The experiment is done using the advertisements and user data from Morgenstern, a financial social website that focuses on the advertisement agency. The experiment results show that CCAM provides better performance than ITCC since it consider the use of augmented data during clustering.
This presentation covers statistics, its importance, its applications, branches of statistics, basic concepts used in statistics, data sampling, types of sampling,types of data and collection of data.
THE IMPORTANCE OF MARTIAN ATMOSPHERE SAMPLE RETURN.Sérgio Sacani
The return of a sample of near-surface atmosphere from Mars would facilitate answers to several first-order science questions surrounding the formation and evolution of the planet. One of the important aspects of terrestrial planet formation in general is the role that primary atmospheres played in influencing the chemistry and structure of the planets and their antecedents. Studies of the martian atmosphere can be used to investigate the role of a primary atmosphere in its history. Atmosphere samples would also inform our understanding of the near-surface chemistry of the planet, and ultimately the prospects for life. High-precision isotopic analyses of constituent gases are needed to address these questions, requiring that the analyses are made on returned samples rather than in situ.
Cancer cell metabolism: special Reference to Lactate PathwayAADYARAJPANDEY1
Normal Cell Metabolism:
Cellular respiration describes the series of steps that cells use to break down sugar and other chemicals to get the energy we need to function.
Energy is stored in the bonds of glucose and when glucose is broken down, much of that energy is released.
Cell utilize energy in the form of ATP.
The first step of respiration is called glycolysis. In a series of steps, glycolysis breaks glucose into two smaller molecules - a chemical called pyruvate. A small amount of ATP is formed during this process.
Most healthy cells continue the breakdown in a second process, called the Kreb's cycle. The Kreb's cycle allows cells to “burn” the pyruvates made in glycolysis to get more ATP.
The last step in the breakdown of glucose is called oxidative phosphorylation (Ox-Phos).
It takes place in specialized cell structures called mitochondria. This process produces a large amount of ATP. Importantly, cells need oxygen to complete oxidative phosphorylation.
If a cell completes only glycolysis, only 2 molecules of ATP are made per glucose. However, if the cell completes the entire respiration process (glycolysis - Kreb's - oxidative phosphorylation), about 36 molecules of ATP are created, giving it much more energy to use.
IN CANCER CELL:
Unlike healthy cells that "burn" the entire molecule of sugar to capture a large amount of energy as ATP, cancer cells are wasteful.
Cancer cells only partially break down sugar molecules. They overuse the first step of respiration, glycolysis. They frequently do not complete the second step, oxidative phosphorylation.
This results in only 2 molecules of ATP per each glucose molecule instead of the 36 or so ATPs healthy cells gain. As a result, cancer cells need to use a lot more sugar molecules to get enough energy to survive.
Unlike healthy cells that "burn" the entire molecule of sugar to capture a large amount of energy as ATP, cancer cells are wasteful.
Cancer cells only partially break down sugar molecules. They overuse the first step of respiration, glycolysis. They frequently do not complete the second step, oxidative phosphorylation.
This results in only 2 molecules of ATP per each glucose molecule instead of the 36 or so ATPs healthy cells gain. As a result, cancer cells need to use a lot more sugar molecules to get enough energy to survive.
introduction to WARBERG PHENOMENA:
WARBURG EFFECT Usually, cancer cells are highly glycolytic (glucose addiction) and take up more glucose than do normal cells from outside.
Otto Heinrich Warburg (; 8 October 1883 – 1 August 1970) In 1931 was awarded the Nobel Prize in Physiology for his "discovery of the nature and mode of action of the respiratory enzyme.
WARNBURG EFFECT : cancer cells under aerobic (well-oxygenated) conditions to metabolize glucose to lactate (aerobic glycolysis) is known as the Warburg effect. Warburg made the observation that tumor slices consume glucose and secrete lactate at a higher rate than normal tissues.
This pdf is about the Schizophrenia.
For more details visit on YouTube; @SELF-EXPLANATORY;
https://www.youtube.com/channel/UCAiarMZDNhe1A3Rnpr_WkzA/videos
Thanks...!
Observation of Io’s Resurfacing via Plume Deposition Using Ground-based Adapt...Sérgio Sacani
Since volcanic activity was first discovered on Io from Voyager images in 1979, changes
on Io’s surface have been monitored from both spacecraft and ground-based telescopes.
Here, we present the highest spatial resolution images of Io ever obtained from a groundbased telescope. These images, acquired by the SHARK-VIS instrument on the Large
Binocular Telescope, show evidence of a major resurfacing event on Io’s trailing hemisphere. When compared to the most recent spacecraft images, the SHARK-VIS images
show that a plume deposit from a powerful eruption at Pillan Patera has covered part
of the long-lived Pele plume deposit. Although this type of resurfacing event may be common on Io, few have been detected due to the rarity of spacecraft visits and the previously low spatial resolution available from Earth-based telescopes. The SHARK-VIS instrument ushers in a new era of high resolution imaging of Io’s surface using adaptive
optics at visible wavelengths.
Seminar of U.V. Spectroscopy by SAMIR PANDASAMIR PANDA
Spectroscopy is a branch of science dealing the study of interaction of electromagnetic radiation with matter.
Ultraviolet-visible spectroscopy refers to absorption spectroscopy or reflect spectroscopy in the UV-VIS spectral region.
Ultraviolet-visible spectroscopy is an analytical method that can measure the amount of light received by the analyte.
Earliest Galaxies in the JADES Origins Field: Luminosity Function and Cosmic ...Sérgio Sacani
We characterize the earliest galaxy population in the JADES Origins Field (JOF), the deepest
imaging field observed with JWST. We make use of the ancillary Hubble optical images (5 filters
spanning 0.4−0.9µm) and novel JWST images with 14 filters spanning 0.8−5µm, including 7 mediumband filters, and reaching total exposure times of up to 46 hours per filter. We combine all our data
at > 2.3µm to construct an ultradeep image, reaching as deep as ≈ 31.4 AB mag in the stack and
30.3-31.0 AB mag (5σ, r = 0.1” circular aperture) in individual filters. We measure photometric
redshifts and use robust selection criteria to identify a sample of eight galaxy candidates at redshifts
z = 11.5 − 15. These objects show compact half-light radii of R1/2 ∼ 50 − 200pc, stellar masses of
M⋆ ∼ 107−108M⊙, and star-formation rates of SFR ∼ 0.1−1 M⊙ yr−1
. Our search finds no candidates
at 15 < z < 20, placing upper limits at these redshifts. We develop a forward modeling approach to
infer the properties of the evolving luminosity function without binning in redshift or luminosity that
marginalizes over the photometric redshift uncertainty of our candidate galaxies and incorporates the
impact of non-detections. We find a z = 12 luminosity function in good agreement with prior results,
and that the luminosity function normalization and UV luminosity density decline by a factor of ∼ 2.5
from z = 12 to z = 14. We discuss the possible implications of our results in the context of theoretical
models for evolution of the dark matter halo mass function.
Nutraceutical market, scope and growth: Herbal drug technologyLokesh Patil
As consumer awareness of health and wellness rises, the nutraceutical market—which includes goods like functional meals, drinks, and dietary supplements that provide health advantages beyond basic nutrition—is growing significantly. As healthcare expenses rise, the population ages, and people want natural and preventative health solutions more and more, this industry is increasing quickly. Further driving market expansion are product formulation innovations and the use of cutting-edge technology for customized nutrition. With its worldwide reach, the nutraceutical industry is expected to keep growing and provide significant chances for research and investment in a number of categories, including vitamins, minerals, probiotics, and herbal supplements.
Modeling Social Data, Lecture 2: Introduction to Counting
1. Introduction to Counting
APAM E4990
Modeling Social Data
Jake Hofman
Columbia University
January 30, 2013
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 1 / 28
5. Why counting?
?p( y
support
| x1, x2, x3, . . .
age, sex, race, party
)
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 4 / 28
6. Why counting?
Problem:
Traditionally difficult to obtain reliable estimates due to small
sample sizes or sparsity
(e.g., ∼ 100 age × 2 sex × 5 race × 3 party = 3000 groups,
but typical surveys collect ∼ 1,000s of responses)
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 5 / 28
7. Why counting?
Potential solution:
Sacrifice granularity for precision, by binning observations into
larger, but fewer, groups
(e.g., bin age into a few groups: 18-29, 30-49, 50-64, 65+)
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 5 / 28
8. Why counting?
Potential solution:
Develop more sophisticated methods that generalize well from
small samples
(e.g., fit a model: support ∼ β0 + β1age + β2age2 + . . .)
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 5 / 28
9. Why counting?
(Partial) solution:
Obtain larger samples through other means, so we can just count
and divide to make estimates via relative frequencies
(e.g., with ∼ 1M responses, we have 100s per group and can
estimate support within a few percentage points)
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 6 / 28
10. Why counting?
The good:
Shift away from sophisticated statistical methods on small samples
to simple methods on large samples
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 7 / 28
11. Why counting?
The bad:
Even simple methods (e.g., counting) are computationally
challenging at large scales
(1M is easy, 1B a bit less so, 1T gets interesting)
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 7 / 28
12. Why counting?
Claim:
Solving the counting problem at scale enables you to investigate
many interesting questions in the social sciences
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 7 / 28
13. Learning to count
This week:
Counting at small/medium scales on a single machine
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 8 / 28
14. Learning to count
This week:
Counting at small/medium scales on a single machine
Following weeks:
Counting at large scales in parallel
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 8 / 28
15. Counting, the easy way
Split / Apply / Combine1
http://bit.ly/sactutorial
• Load dataset into memory
• Split: Arrange observations into groups of interest
• Apply: Compute distributions and statistics within each group
• Combine: Collect results across groups
1
http://bit.ly/splitapplycombine
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 9 / 28
16. The generic group-by operation
Split / Apply / Combine
for each observation as (group, value):
place value in bucket for corresponding group
for each group:
apply a function over values in bucket
output group and result
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 10 / 28
17. The generic group-by operation
Split / Apply / Combine
for each observation as (group, value):
place value in bucket for corresponding group
for each group:
apply a function over values in bucket
output group and result
Useful for computing arbitrary within-group statistics when we
have required memory
(e.g., conditional distribution, median, etc.)
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 10 / 28
23. Example: Movielens
1 2 3 4 5
Mean Rating by Movie
Density
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 15 / 28
24. Example: Movielens
group by movie id
for each group:
compute average rating
1 2 3 4 5
Mean Rating by Movie
Density
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 16 / 28
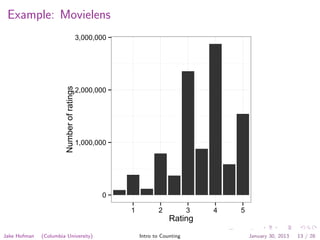
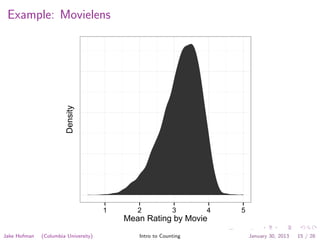
26. Example: Movielens
0%
25%
50%
75%
100%
0 3,000 6,000 9,000
Movie Rank
CDF
group by movie id
for each group:
count # ratings
sort by group size
cumulatively sum group sizes
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 18 / 28
28. Example: Movielens
join movie ranks to ratings
group by user id
for each group:
compute median movie rank
0
2,000
4,000
6,000
8,000
100 10,000
User eccentricity
Numberofusers
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 20 / 28
29. Example: Anatomy of the long tail
Dataset Users Items Rating levels Observations
Movielens 100K 10K 10 10M
Netflix 500K 20K 5 100M
What do we do when the full dataset exceeds available memory?
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 21 / 28
30. Example: Anatomy of the long tail
Dataset Users Items Rating levels Observations
Movielens 100K 10K 10 10M
Netflix 500K 20K 5 100M
What do we do when the full dataset exceeds available memory?
Sampling?
Unreliable estimates for rare groups
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 21 / 28
31. Example: Anatomy of the long tail
Dataset Users Items Rating levels Observations
Movielens 100K 10K 10 10M
Netflix 500K 20K 5 100M
What do we do when the full dataset exceeds available memory?
Random access from disk?
1000x more storage, but 1000x slower2
2
Numbers every programmer should know
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 21 / 28
32. Example: Anatomy of the long tail
Dataset Users Items Rating levels Observations
Movielens 100K 10K 10 10M
Netflix 500K 20K 5 100M
What do we do when the full dataset exceeds available memory?
Streaming
Read data one observation at a time, storing only needed state
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 21 / 28
33. The combinable group-by operation
Streaming
for each observation as (group, value):
if new group:
initialize result
update result for corresponding group as function of
existing result and current value
for each group:
output group and result
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 22 / 28
34. The combinable group-by operation
Streaming
for each observation as (group, value):
if new group:
initialize result
update result for corresponding group as function of
existing result and current value
for each group:
output group and result
Useful for computing a subset of within-group statistics with a
limited memory footprint
(e.g., min, mean, max, variance, etc.)
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 22 / 28
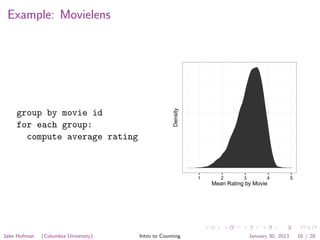
36. Example: Movielens
for each rating:
totals[movie id] += rating
counts[movie id]++
for each group:
totals[movie id] /
counts[movie id]
1 2 3 4 5
Mean Rating by Movie
Density
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 24 / 28
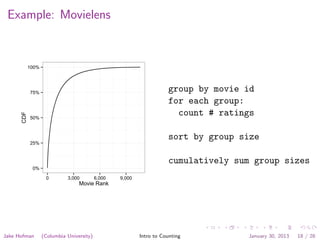
37. Yet another group-by operation
Per-group histograms
for each observation as (group, value):
histogram[group][value]++
for each group:
compute result as a function of histogram
output group and result
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 25 / 28
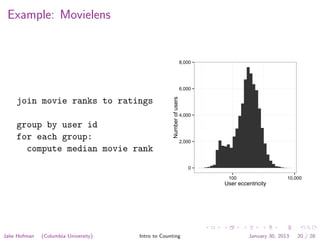
38. Yet another group-by operation
Per-group histograms
for each observation as (group, value):
histogram[group][value]++
for each group:
compute result as a function of histogram
output group and result
We can recover arbitrary statistics if we can afford to store counts
of all distinct values within in each group
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 25 / 28
39. The group-by operation
For arbitrary input data:
Memory Scenario Distributions Statistics
N Small dataset Yes General
V*G Small distributions Yes General
G Small # groups No Combinable
V Small # outcomes No No
1 Large # both No No
N = total number of observations
G = number of distinct groups
V = largest number of distinct values within group
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 26 / 28
40. Examples (w/ 8GB RAM)
Median rating by movie for Netflix
N ∼ 100M ratings
G ∼ 20K movies
V ∼ 10 half-star values
V *G ∼ 200K, store per-group histograms for arbitrary statistics
(scales to arbitrary N, if you’re patient)
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 27 / 28
41. Examples (w/ 8GB RAM)
Median rating by video for YouTube
N ∼ 10B ratings
G ∼ 1B videos
V ∼ 10 half-star values
V *G ∼ 10B, fails because per-group histograms are too large to
store in memory
G ∼ 1B, but no (exact) calculation for streaming median
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 27 / 28
42. Examples (w/ 8GB RAM)
Mean rating by video for YouTube
N ∼ 10B ratings
G ∼ 1B videos
V ∼ 10 half-star values
G ∼ 1B, use streaming to compute combinable statistics
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 27 / 28
43. The group-by operation
For pre-grouped input data:
Memory Scenario Distributions Statistics
N Small dataset Yes General
V*G Small distributions Yes General
G Small # groups No Combinable
V Small # outcomes Yes General
1 Large # both No Combinable
N = total number of observations
G = number of distinct groups
V = largest number of distinct values within group
Jake Hofman (Columbia University) Intro to Counting January 30, 2013 28 / 28
