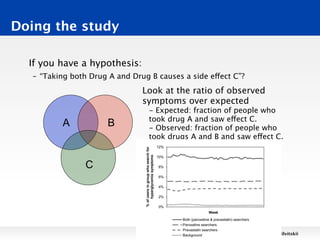
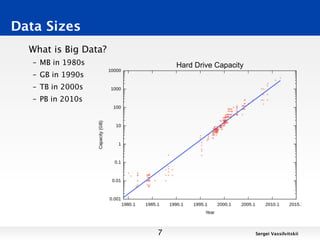
This document discusses techniques for finding the intersection between two large datasets efficiently. It begins by noting that while computers can perform billions of operations per second, datasets are huge, ranging from terabytes to petabytes in size. Two techniques for finding intersections are examined: scanning and sorting. Scanning has a runtime of O(n2) while sorting has a runtime of O(n log n), making sorting faster. Hashing is proposed as an even faster alternative with a runtime of O(n). Reasoning about algorithmic runtimes and how they scale with input size is discussed.

1. Counting Fast
(Part I)
Sergei Vassilvitskii
Columbia University
Computational Social Science
March 8, 2013

2. Computers are fast!
Servers:
– 3.5+ Ghz
Laptops:
– 2.0 - 3 Ghz
Phones:
– 1.0-1.5 GHz
Overall: Executes billions of operations per second!
2 Sergei Vassilvitskii

3. But Data is Big!
Datasets are huge:
– Social Graphs (Billions of nodes, each with hundreds of edges)
• Terabytes (million million bytes)
– Pictures, Videos, associated metadata:
• Petabytes (million billion bytes!)
3 Sergei Vassilvitskii

4. Computers are getting faster
Moore’s law (1965!):
– Number of transistors on a chip doubles every two years.
4 Sergei Vassilvitskii

5. Computers are getting faster
Moore’s law (1965!):
– Number of transistors on a chip doubles every two years.
For a few decades:
– The speed of chips doubled every 24 months.
Now:
– The number of cores doubling
– Speed staying roughly the same
5 Sergei Vassilvitskii

6. But Data is Getting Even Bigger
Unknown author, 1981 (?):
– “640K ought to be enough for anyone”
Eric Schmidt, March 2013:
– “There were 5 exabytes of information created between the dawn of
civilization through 2003, but that much information is now created
every 2 days, and the pace is increasing.”
6 Sergei Vassilvitskii

7. Data Sizes
What is Big Data?
– MB in 1980s Hard Drive Capacity
– GB in 1990s
– TB in 2000s
– PB in 2010s
7 Sergei Vassilvitskii

8. Working with Big Data
Two datasets of numbers:
– Want to find the intersection (common values)
– Why?
• Data cleaning (these are missing values)
• Data mining (these are unique in some way)
8 Sergei Vassilvitskii

9. Working with Big Data
Two datasets of numbers:
– Want to find the intersection (common values)
– Why?
• Data cleaning (these are missing values)
• Data mining (these are unique in some way)
– How long should it take?
• Each dataset has 10 numbers?
• Each dataset has 10k numbers?
• Each dataset has 10M numbers?
• Each dataset has 10B numbers?
• Each dataset has 10T numbers?
9 Sergei Vassilvitskii

10. How to Find Intersections?
10 Sergei Vassilvitskii

11. Idea 1: Scan
Look at every number in list 1:
– Scan through dataset 2, see if you find a match
common_elements = 0
for number in dataset1:
for number2 in dataset2:
if number1 == number2:
common_elements +=1
11 Sergei Vassilvitskii

12. Idea 1: Scanning
For each element in dataset 1, scan through dataset 2, see if it’s present
common_elements = 0
for number in dataset1:
for number2 in dataset2:
if number1 == number2:
common_elements +=1
Analysis: Number of times if statement executed?
– |dataset2| for every iteration of outer loop
– |dataset1| * |dataset2| in total
12 Sergei Vassilvitskii

13. Idea 1: Scanning
Analysis: Number of times if statement executed?
– |dataset2| for every iteration of outer loop
– |dataset1| * |dataset2| in total
Running time:
– 100M * 100M = 1016 comparisons in total
– At 1B (109) comparisons / second
13 Sergei Vassilvitskii

14. Idea 1: Scanning
Analysis: Number of times if statement executed?
– |dataset2| for every iteration of outer loop
– |dataset1| * |dataset2| in total
Running time:
– 100M * 100M = 1016 comparisons in total
– At 1B (109) comparisons / second
– 107 seconds ~ 4 months!
– Even with 1000 computers: 104 seconds -- 2.5 hours!
14 Sergei Vassilvitskii

15. Idea 2: Sorting
Suppose both sets are sorted
– Keep pointers to each
– Check for match, increase the smaller pointer
[Blackboard]
15 Sergei Vassilvitskii

16. Idea 2: Sorting
sorted1 = sorted(dataset1)
sorted2 = sorted(dataset2)
pointer1, pointer2 = 0
common_elements = 0
while pointer1 < size(dataset1) and pointer2 < size(dataset2):
if sorted[pointer1] == sorted[pointer2]:
common_elements+=1
pointer1+=1; pointer2+=1
else if sorted[pointer1] < sorted[pointer2]:
pointer1+=1
else:
pointer2+=1
Analysis:
– Number of times if statement executed?
– Increment a counter each time: |dataset1|+|dataset2|
16 Sergei Vassilvitskii

17. Idea 2: Sorting
Analysis:
– Number of times if statement executed?
– Increment a counter each time: |dataset1|+|dataset2|
Running time:
– At most 100M + 100M comparisons
– At 1B comparisons/second ~ 0.2 seconds
– Plus cost of sorting! ~1 second per list
– Total time = 2.2 seconds
17 Sergei Vassilvitskii

18. Reasoning About Running Times (1)
Worry about the computation as a function of input size:
– “If I double my input size, how much longer will it take?”
• Linear time (comparisons after sorting): twice as long!
• Quadratic time (scan): four (22) times as long
• Cubic time (very slow): 8 (23) time as long
• Exponential time (untenable):
• Sublinear time (uses sampling, skips over input)
18 Sergei Vassilvitskii

19. Reasoning About Running Times (2)
Worry about the computation as a function of input size.
Worry about order of magnitude, not exact running time:
– Difference between 2 seconds and 4 seconds much smaller than
between 2 seconds and 3 months!
• The scan algorithm does more work in the while loop (but only a constant more
work) -- 3 comparisons instead of 1.
• Therefore, still call it linear time
19 Sergei Vassilvitskii

20. Reasoning about running time
Worry about the computation as a function of input size.
Worry about order of magnitude, not exact running time.
Captured by the Order notation: O(.)
– For an input of size n, approximately how long will it take?
– Scan: O(n2)
– Comparisons after sorted: O(n)
20 Sergei Vassilvitskii

21. Reasoning about running time
Worry about the computation as a function of input size.
Worry about order of magnitude, not exact running time.
Captured by the Order notation: O(.)
– For an input of size n, approximately how long will it take?
– Scan: O(n2)
– Comparisons after sorted: O(n)
– Sorting = O(n log n)
• Slightly more than n,
• But much less than n2.
21 Sergei Vassilvitskii

22. Avoiding Sort: Hashing
Idea 3.
– Store each number in list1 in a location unique to it
– For each element in list2, check if its unique location is empty
[Blackboard]
22 Sergei Vassilvitskii

23. Idea 3: Hashing
table = {}
for i in range(total):
table.add(dataset1[i])
common_elements = 0
for i in range(total):
if (table.has(dataset2[i])):
common_elements+=1
Analysis:
– Number of additions to the table: |dataset1|
– Number of comparisons: |dataset2|
– If Additions to the table and comparisons are 1B/second
– Total running time is: 0.2s
23 Sergei Vassilvitskii

24. Lots of Details
Hashing, Sorting, Scanning:
– All have their advantages
– Scanning: in place, just passing through the data
– Sorting: in place (no extra storage), much faster
– Hashing: not in place, even faster
24 Sergei Vassilvitskii

25. Lots of Details
Hashing, Sorting, Scanning:
– All have their advantages
– Scanning: in place, just passing through the data
– Sorting: in place (no extra storage), much faster
– Hashing: not in place, even faster
Reasoning about algorithms:
– Non trivial (and hard!)
– A large part of computer science
– Luckily mostly abstracted
25 Sergei Vassilvitskii

26. Break
26 Sergei Vassilvitskii

27. Distributed Computation
Working with large datasets:
– Most datasets are skewed
– A few keys are responsible for most of the data
– Must take skew into account, since averages are misleading
27 Sergei Vassilvitskii

28. Additional Cost
Communication cost
– Prefer to do more on a single machine (even if it’s doing more work) to
constantly communicating
– Why? If you have 1000 machines talking to 1000 machines --- that’s
1M channels of communication
– The overall communication cost grows quadratically, which we have
seen does not scale...
28 Sergei Vassilvitskii

29. Analysis at Scale
29 Sergei Vassilvitskii

30. Doing the study
Suppose you had the data available. What would you do?
If you have a hypothesis:
– “Taking both Drug A and Drug B causes a side effect C”?
30 Sergei Vassilvitskii

31. Doing the study
If you have a hypothesis:
– “Taking both Drug A and Drug B causes a side effect C”?
Look at the ratio of observed
symptoms over expected
- Expected: fraction of people who
took drug A and saw effect C.
A B - Observed: fraction of people who
took drugs A and B and saw effect C.
C
31 Sergei Vassilvitskii

32. Doing the study
If you have a hypothesis:
– “Taking both Drug A and Drug B causes a side effect C”?
Look at the ratio of observed
symptoms over expected
- Expected: fraction of people who
took drug A and saw effect C.
A B - Observed: fraction of people who
took drugs A and B and saw effect C.
This is just counting!
C
32 Sergei Vassilvitskii

33. Doing the study
Suppose you had the data available. What would you do?
Discovering hypotheses to test:
– Many pairs of drugs, some co-occur very often
– Some side effects are already known
33 Sergei Vassilvitskii