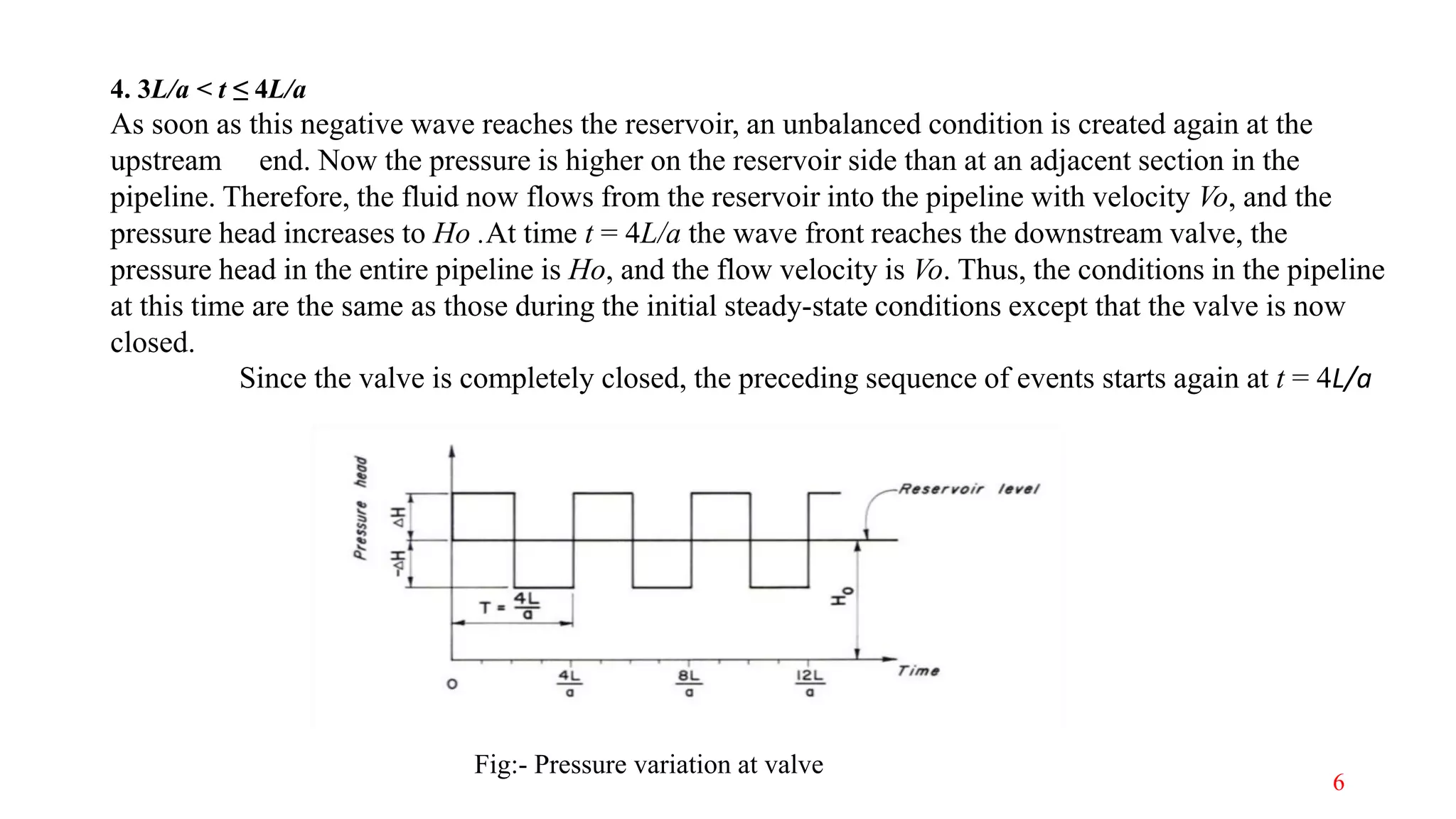
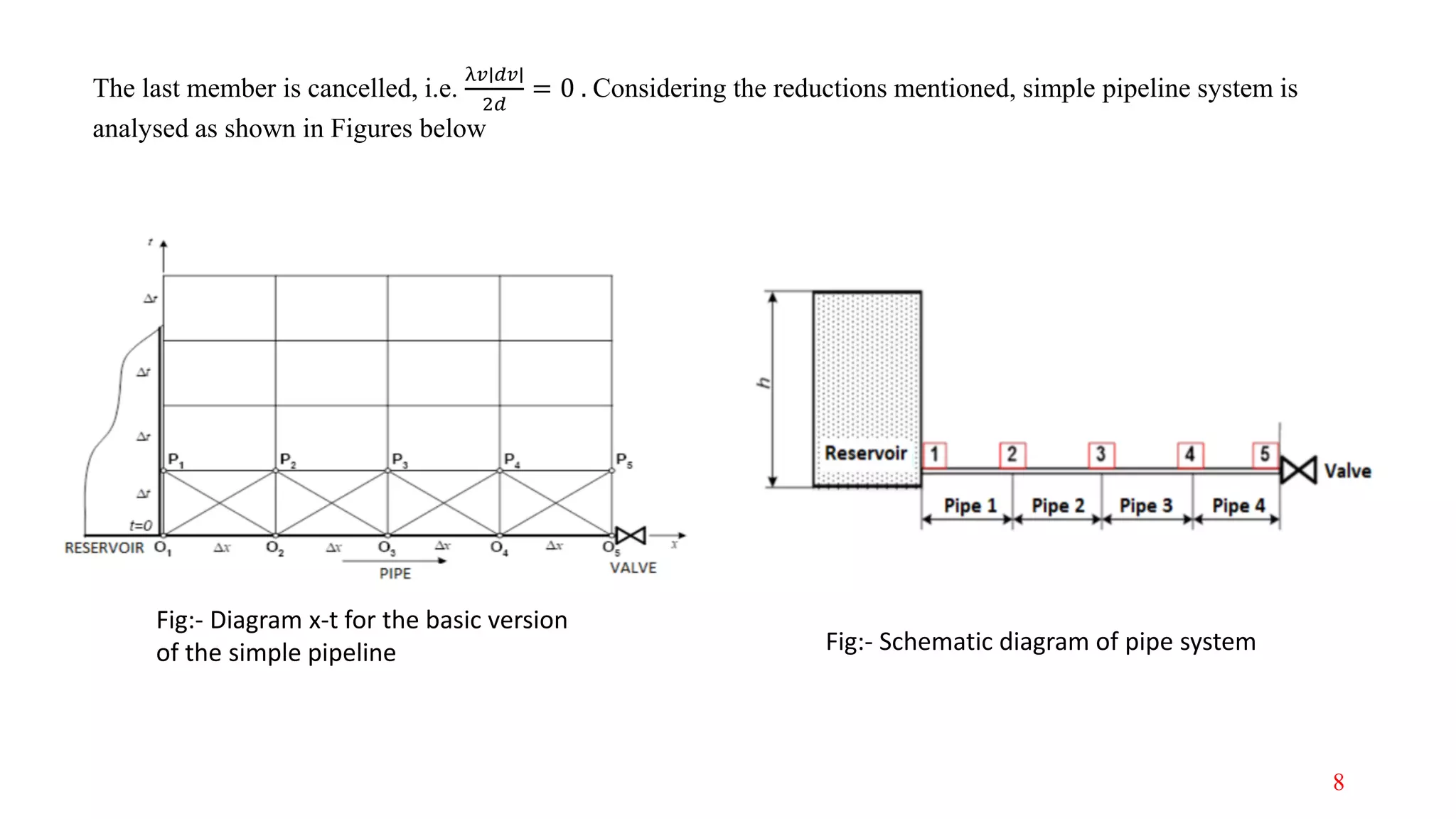
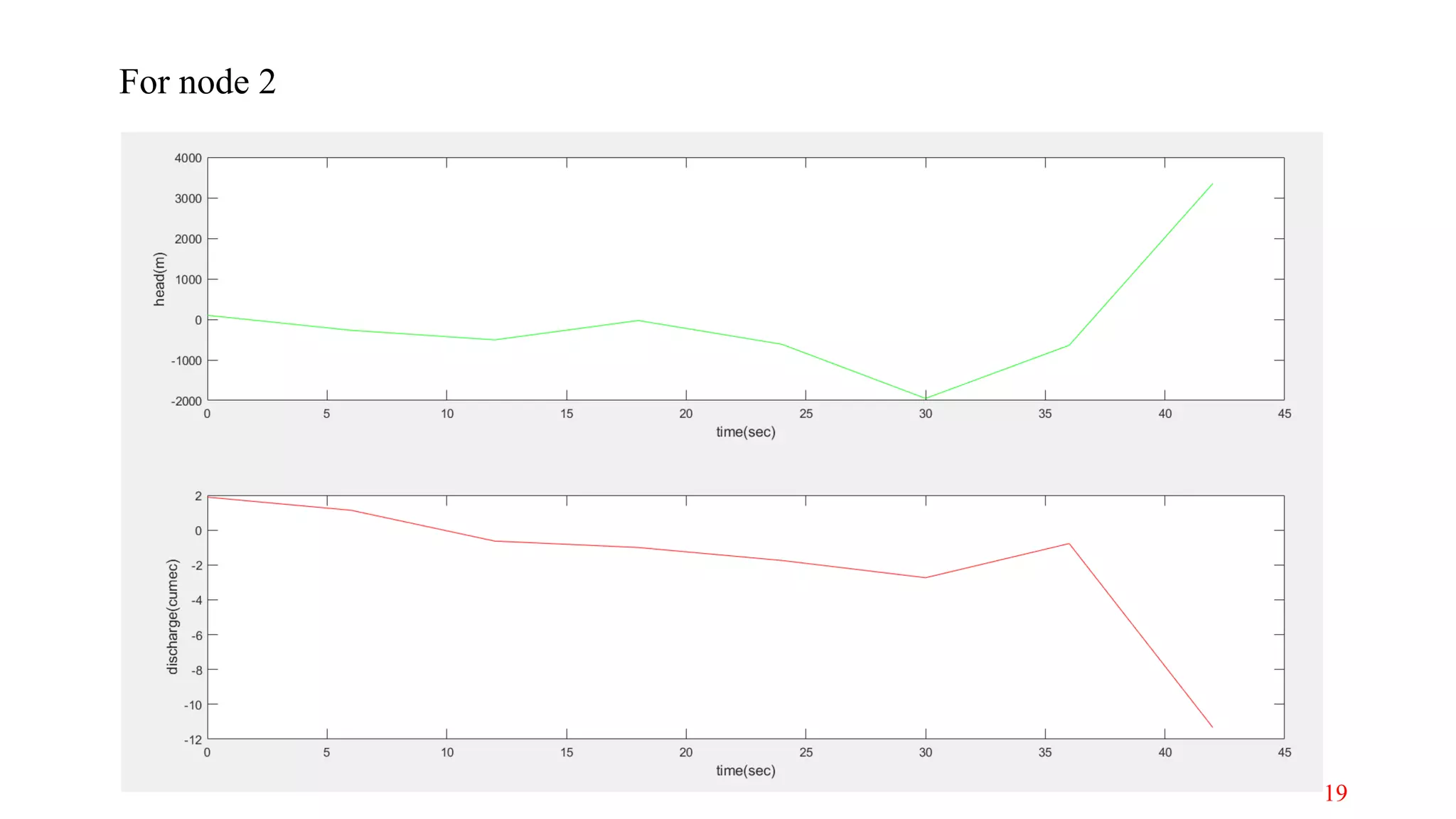
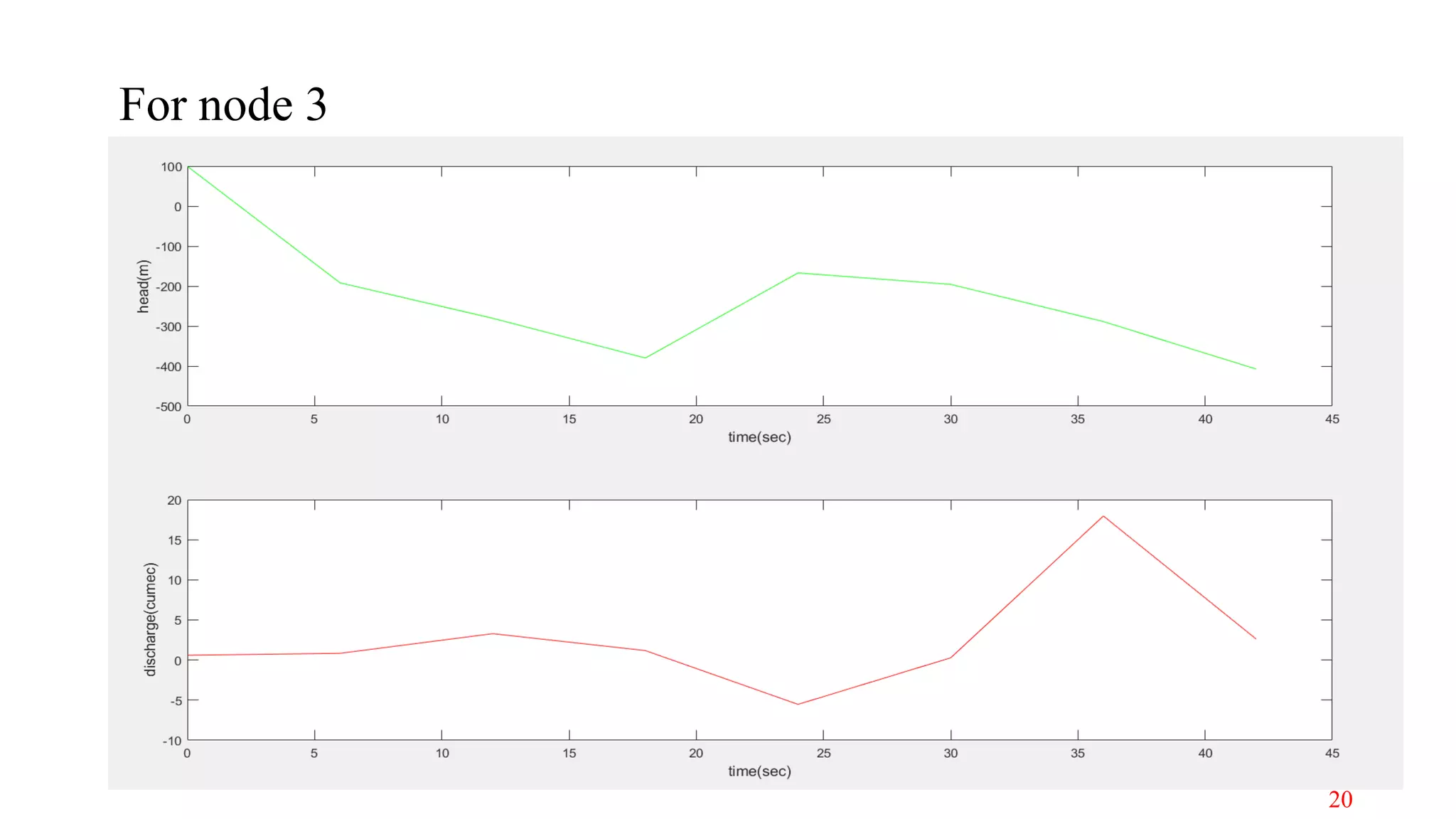
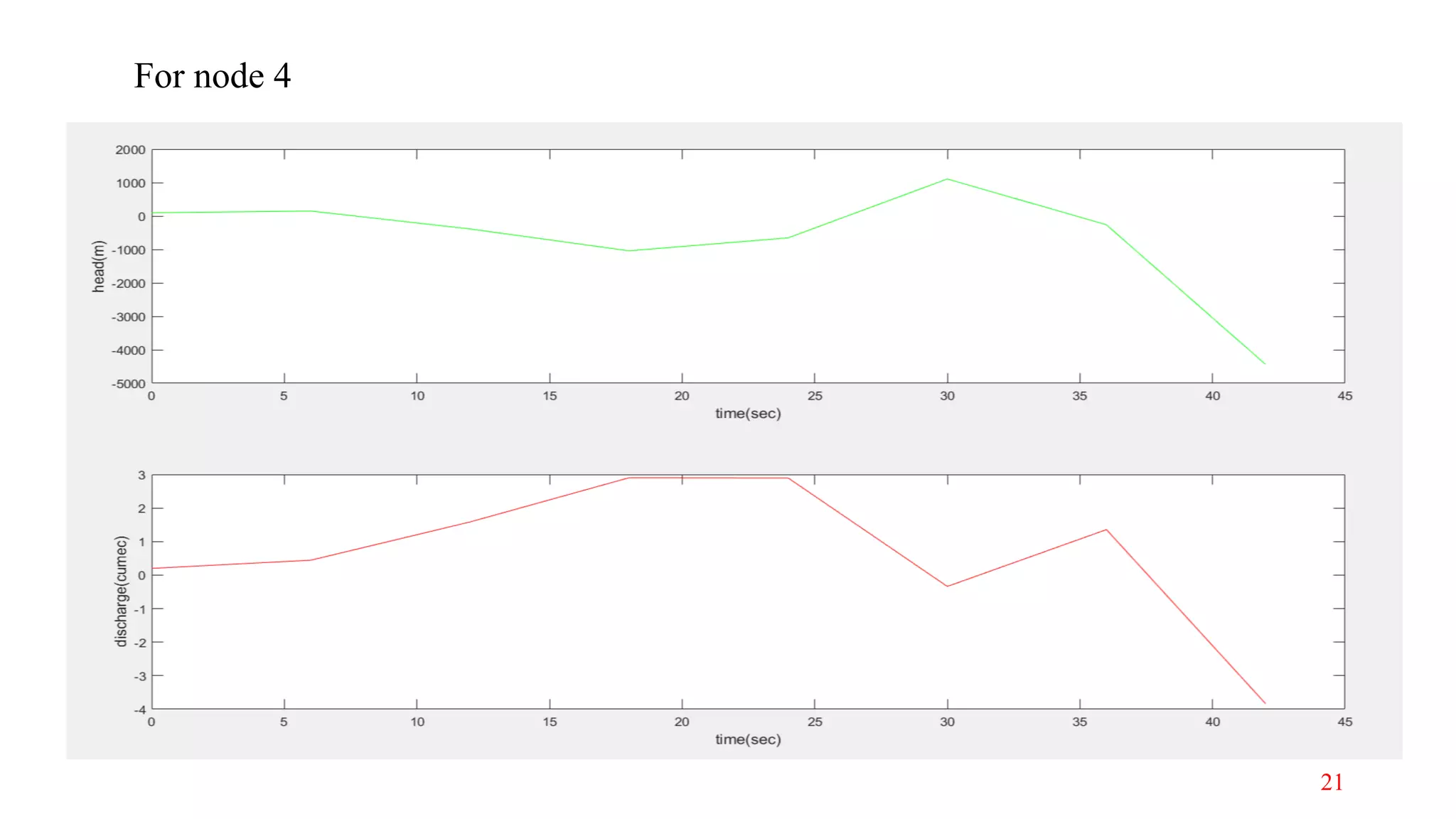
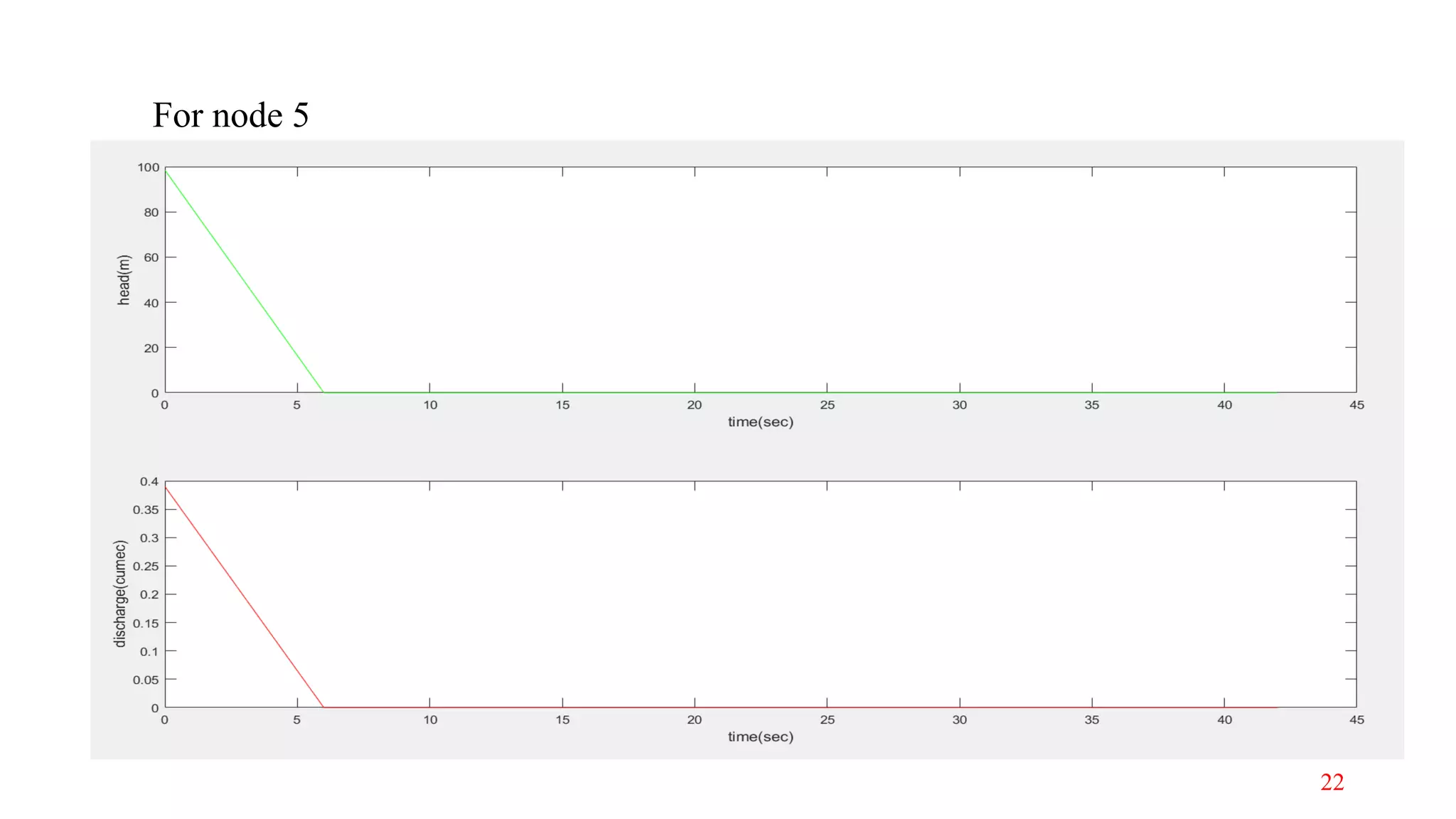
The document discusses the modeling of transient fluid flow in a simple pipeline system, outlining concepts such as transient flow, various methods for formulation, and common causes of transient flow events. It highlights the importance of understanding how sudden changes, like valve closures, affect pressure and flow, leading to phenomena such as surges and water hammer. The analysis includes numerical methods, specifically the Lax scheme, for simulating fluid dynamics within the pipeline system.

1. MODELING OF TRANSIENT FLUID
FLOW IN THE SIMPLE PIPELINE
SYSTEM
Submitted by:-
Aniruddha Singha (184104602)

2. What is Transient Flow
 A transient is a temporary flow and pressure condition that occurs in a hydraulic system
between an initial steady-state condition and a final steady-state condition;
 When velocity changes rapidly in response to the operation of a flow-control device(for
instance, a valve closure or pump start), the compressibility of the liquid and the elasticity of
the pipeline cause a transient pressure wave to propagate throughout the system;
 In general, transients resulting from relatively slow changes in flow rate are referred to as
surges, and those resulting from more rapid changes in flow rate are referred to as water
hammer events. Surges in pressurized systems are different than tidal or storm
surges, flood waves, or dam breaks, which can occur in open-water bodies;
 In general engineering practice, the terms surge, transient and water hammer are synonymous.
1

3. Methods for Formulation of transient flow
• Various methods have been developed to solve transient flow in pipes. These range from approximate equations to
numerical solutions of the nonlinear Navier-Stokes equations:
I. Arithmetic method—Assumes that flow stops instantaneously (in less than the characteristic time, 2L/a),
cannot handle water column separation directly, and neglects friction (Joukowski, 1898; Allievi, 1902).
II. Graphical method—Neglects friction in its theoretical development but includes a means of accounting for it
through a correction (Parmakian, 1963). It is time consuming and not suited to solving networks or pipelines with
complex profiles.
III. Method of Characteristics (MOC)—Most widely used and tested approach, with support for complex boundary
conditions and friction and vaporous cavitation models. It converts the partial differential equations(PDEs) of
continuity and momentum (e.g., Navier-Stokes) into ordinary differential equations that are solved algebraically
along lines called characteristics.
2

4. Common causes of transient flow
The most common causes of transient initiation, or source devices, are all moving
system boundaries.
• Sudden change of external flow demand at a junction due to fire demand or
valve closure;
• Sudden valve opening or closure;
• Pump Failure;
• Valves can be opened or closed with
the time varying change.
Fig:- Common Causes of Hydraulic Transients 3

5. Valves : A valve can start, change, or stop flow very suddenly. Energy
conservations increase or decrease in proportion to a valve’s closing or opening
rate and position , or stroke . Orifices can be used to throttle flow instead of a
partially open valve . Valves can also allow air into a pipeline and/or expel it,
typically at local high points.
(The problem that has been formulated for transient flow in pipelines is
due to closure of valve).
In pressurized networks, a steady-state condition or transient event at one
point in the system can affect all other parts of the system. Consequently,
computer models must consider every pipe that is directly connected to a
pressurized system, regardless of administrative or political boundaries.
4

6. Wave Propagation
The sequence of events following valve closure may be divided into four parts (Fig) as follows:
1. 0 < t ≤ L/a
When the valve is closed the flow velocity at the valve becomes zero. This increases the pressure at the valve by ΔH = -(a/g) ΔV.
and a positive pressure wave propagates towards the reservoir at the upstream. If a is the velocity of the pressure wave and L is
the length of the pipeline, then the wave front reaches the upstream reservoir at time t = L/a. At this time, along the entire length
of the pipeline, the pipe is expanded, the flow velocity is zero, and the pressure head is Ho + ΔH .
2. L/a < t ≤ 2L/a
Just as the wave reaches the upstream reservoir, pressure at a section on the reservoir side is Ho while the pressure at an adjacent
section in the pipe is Ho + ΔH. Because of this difference in pressure, the fluid flows from the pipeline into the reservoir with
velocity -Vo. Thus, the flow velocity at the pipe entrance is reduced from zero to -Vo.
3. 2L/a < t ≤ 3L/a
Since the valve is completely closed, a negative velocity cannot be maintained at the valve. Therefore, the velocity changes
instantaneously from −Vo to 0, the pressure drops to Ho − ΔH, and a negative wave propagates towards the reservoir
Behind this wave front, the pressure is Ho - ΔH and the fluid velocity is zero. The wave front reaches the upstream reservoir
at time t = 3L/a, the pressure head in the entire pipeline is Ho - ΔH, and the fluid velocity is zero.
.
5

7. 4. 3L/a < t ≤ 4L/a
As soon as this negative wave reaches the reservoir, an unbalanced condition is created again at the
upstream end. Now the pressure is higher on the reservoir side than at an adjacent section in the
pipeline. Therefore, the fluid now flows from the reservoir into the pipeline with velocity Vo, and the
pressure head increases to Ho .At time t = 4L/a the wave front reaches the downstream valve, the
pressure head in the entire pipeline is Ho, and the flow velocity is Vo. Thus, the conditions in the pipeline
at this time are the same as those during the initial steady-state conditions except that the valve is now
closed.
Since the valve is completely closed, the preceding sequence of events starts again at t = 4L/a
Fig:- Pressure variation at valve
6

8. Formulation of problem
During the hydraulic shock (water hammer) in the metal pipe, the
velocity c of the pressure disturbance is usually three times greater than
the velocity v of the flow, which therefore, may be ignored in the
characteristic equations
𝑑𝑥
𝑑𝑡
= ± c (1)
In the simplified analysis, fluid viscosity is neglected, which means that
in the equation:
±
𝑔
𝑐
𝑑ℎ
𝑑𝑡
+
𝑑𝑣
𝑑𝑡
+
λ𝑣∣𝑑𝑣∣
2𝑑
= 0 (2)
7

9. The last member is cancelled, i.e.
λ𝑣∣𝑑𝑣∣
2𝑑
= 0 . Considering the reductions mentioned, simple pipeline system is
analysed as shown in Figures below
Fig:- Diagram x-t for the basic version
of the simple pipeline Fig:- Schematic diagram of pipe system
8

10. 1. Continuity Equation for Unsteady Flow
The continuity equation for a fluid is based on the principle of conservation of mass.
The general form of the continuity equation for unsteady fluid flow is as follows :
𝑎2 𝜕𝑄
𝜕𝑥
+ 𝑔𝐴
𝜕𝐻
𝜕𝑡
=0
2. Momentum Equation for Unsteady Flow
The equations of motion for a fluid can be derived from the consideration of the forces
acting on a small element, or control volume, including the shear stresses generated by
the fluid motion and viscosity. The three-dimensional momentum equations of a real
fluid system are known as the Navier-Stokes equations. Since flow perpendicular to
pipe walls is approximately zero, flow in a pipe can be considered one-dimensional, for
which the continuity equation reduces to
𝜕𝑄
𝜕𝑡
+ 𝑔𝐴
𝜕𝐻
𝜕𝑥
+R𝑄 ∣ 𝑄 ∣= 0
9

11. Data used for the problem
• The height of the water pressure in the tank, h = 100m
• The length of the pipe, l = 12000 m
• Number of pipes in the system, n = 4
• Pipe diameter, D = 900mm
• Pressure wave velocity, c = 1200 m/s
• Coefficient of friction resistance, f= 0.022
• Δx=l/n=3000 m
• Δt=6 sec
Initial values
ℎ1=100 at t=0,6,12………
ℎ2= 99.83 at t=0
10

12. ℎ3=99.50 at t=0
ℎ4= 98.70 at t=0
ℎ5=98.5 at t=0
Known values of discharge taken
Q(:,1)=2.63; Q(1,2)=1.89; Q(1,3)=0.6; Q(1,4)=0.2
11

13. Lax Scheme
The numerical scheme used in the problem is the Lax Scheme. This scheme is first-
order accurate, is easy to program and gives satisfactory results although sharp wave
fronts are slightly smeared.
The partial derivatives as follows:-
𝜕𝐻
𝜕𝑡
=
𝐻𝑖
𝑗+1
− 𝐻𝑖
Δ𝑡
𝜕𝑄
𝜕𝑡
=
𝑄𝑖
𝑗+1
− 𝑄𝑖
Δ𝑡
𝜕𝑄
𝜕𝑥
=
𝑄𝑖+1
𝑗
− 𝑄𝑖−1
𝑗
2Δ𝑥
𝜕𝐻
𝜕𝑥
=
𝐻𝑗+1
𝑖
− 𝐻𝑖−1
𝑗
2Δ𝑥 12

14. In which
ഥ𝐻𝑖 = 0.5(𝐻𝑗+1
𝑖
− 𝐻𝑖−1
𝑗
) and
ത𝑄𝑖 = 0.5(𝑄𝑗+1
𝑖
− 𝑄𝑖−1
𝑗
)
Putting the above equations in Continuity and momentum equation we have,
𝐻𝑖
𝑗+1
=0.5(𝐻𝑖−1
𝑗
+𝐻𝑖+1
𝑗
)-0.5
𝑎2
𝑔𝐴
Δ𝑡
Δ𝑥
(𝑄𝑖+1
𝑗
− 𝑄𝑖−1
𝑗
)
and
𝑄𝑖
𝑗+1
=0.5(𝑄𝑖−1
𝑗
+𝑄𝑖+1
𝑗
)-0.5𝑔𝐴
Δ𝑡
Δ𝑥
(𝐻𝑖+1
𝑗
− 𝐻𝑖−1
𝑗
) − RΔ𝑡 ത𝑄𝑖| ത𝑄𝑖|
Fig:- Elementary mesh of
characteristics grid for internal
points
13

15. MATLAB Code
h = 100 ; %The height of the water pressure in the tank,m
l = 12000 ; %The length of the pipe,m
n = 4 ; % Number of pipes in the system,
D = 900/1000; %Pipe diameter, Pipe diameter,mm
c = 1200 ; % velocity of pressure wave,m/s
f= 0.022 ; % Coefficient of friction resistance,
g=9.8 ; %acceleration due to gravity,m/s^2
Q=2.63; %discharge in first node,m^3/s
A=(pi*D^2)/4; %Area of pipe,m^2
V=Q/A; %velocity of water,m/s
%hf=(f*l/n*V^2)/(2*g*D); %%head loss in second node by weisbach equation
hf=.345;
H=100; %head in first node
15

16. h1=99.83; h2=99.50; h3=98.7; h4=98.5; %%% head in each node,m
R=f/(2*D*A^2);
deltax=l/n; %dx
deltat=6; %dt
hh=zeros(8,5);
hh(:,1)=100; hh(1,2)=h1; hh(1,3)=h2; hh(1,4)=h3;
hh(1,5)=h4; %%head loss matrix
qq=zeros(8,5);
qq(:,1)=2.63; qq(1,2)=1.89; qq(1,3)=.6; qq(1,4)=.2;
qq(1,5)=.39; %%discharge matrix
t=0:6:42;
for i=1:7
for j=1:3
hh(i+1,j+1)=hh(i,j)+hh(i,j+2)-(c^2/(2*g*A))*(deltat/deltax)*(qq(i,j)-qq(i,j+2));
for k=1:8
q(k,j+1)=1/2*(qq(k,j)+qq(k,j+2))
end
qq(i+1,j+1)=1/2*(qq(i,j)+qq(i,j+2))-(g*A/2)*(deltat/deltax)*(hh(i,j)-hh(i,j+2))-R *q(i,j+1)*abs(q(i,j+1))*deltat
end
16

17. end
n=3; %node number
subplot(2,1,1);
plot(t',hh(:,n),'g')
xlabel('time(sec)','Fontsize',12);
ylabel('head (m)','Fontsize',12)
subplot(2,1,2);
plot(t',qq(:,n),'r')
xlabel('time(sec)','Fontsize',12);
ylabel('discharge(cumec)','Fontsize',12)
17

18. Output
For node 1
18

19. For node 2
19

20. For node 3
20

21. For node 4
21

22. For node 5
22

23. Conclusion
 The construction of reliable and efficient piping systems represents a large
investment cost due to the number of protective elements to be installed to keep the
system safe from non-stationary phenomena;
 The terms for one-dimensional fluid flow, with the introduction of assumptions and
simplifications, are quite complex, therefore MATLAB programs is used to calculate
fluid flow parameters;
 In the numerical calculations advantage has been taken of the Lax Scheme which
can be used in the cases when frictional effects are very important. In this method
the values of the pressure heads and discharge flows are calculated on the basis of
the mean resistance of elementary pipe sections related to the flow value of the
preceding and following time steps.
14

24. References
 Salmanzadeh M. (1993) “Numerical Method for Modeling Transient Flow in
Distribution Systems”, Islamic Azad University, Shoushtar;
 Vataj G. & Berisha X. (2018) “MODELING OF TRANSIENT FLUID FLOW IN
THE SIMPLE PIPELINE SYSTEM”, University of Prishtina, Pristina, Kosovo;
 Textbook of APPLIED HYDRAULIC TRANSIENTS by M. Hanif Chaudhry.
23