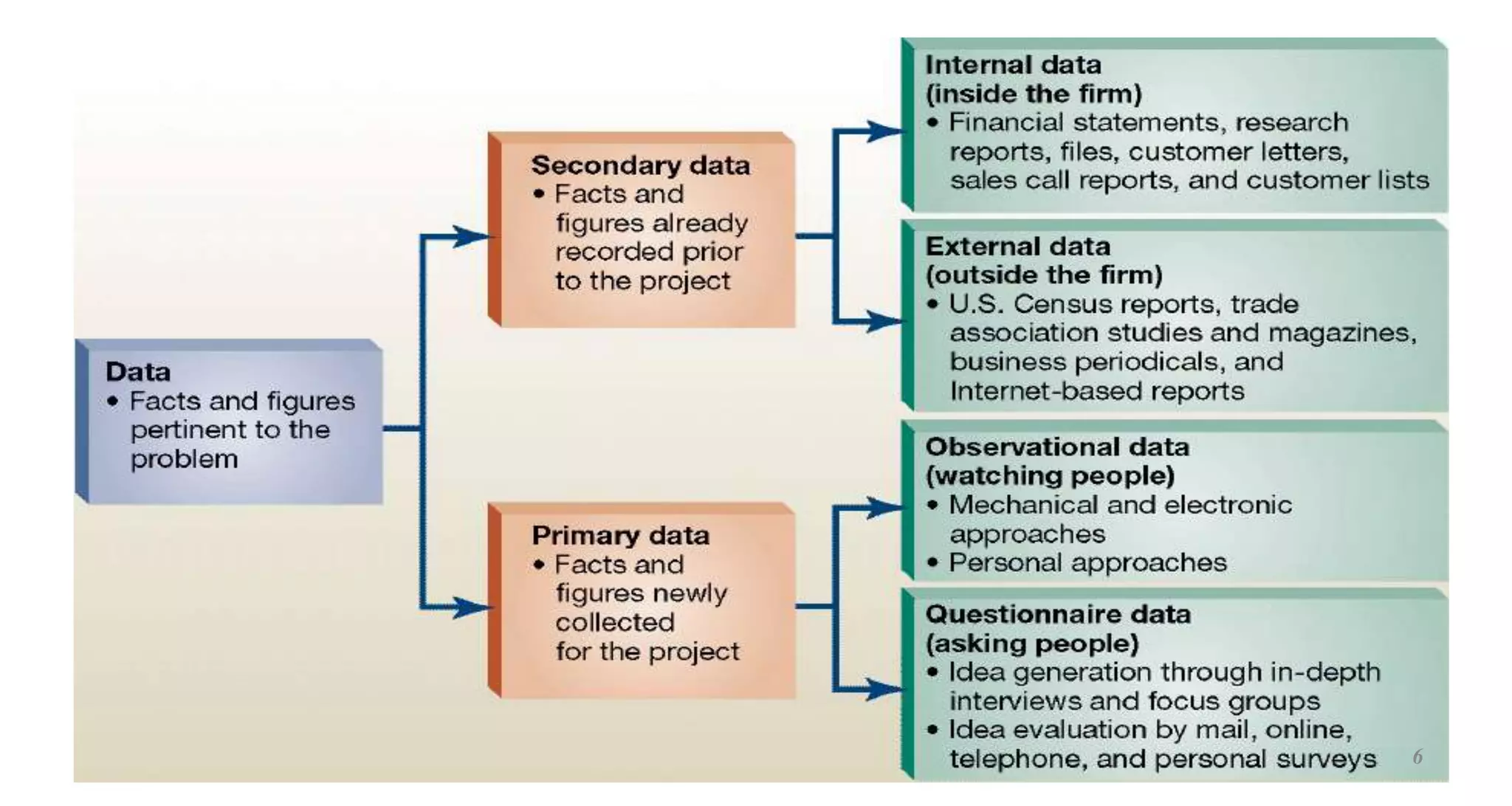
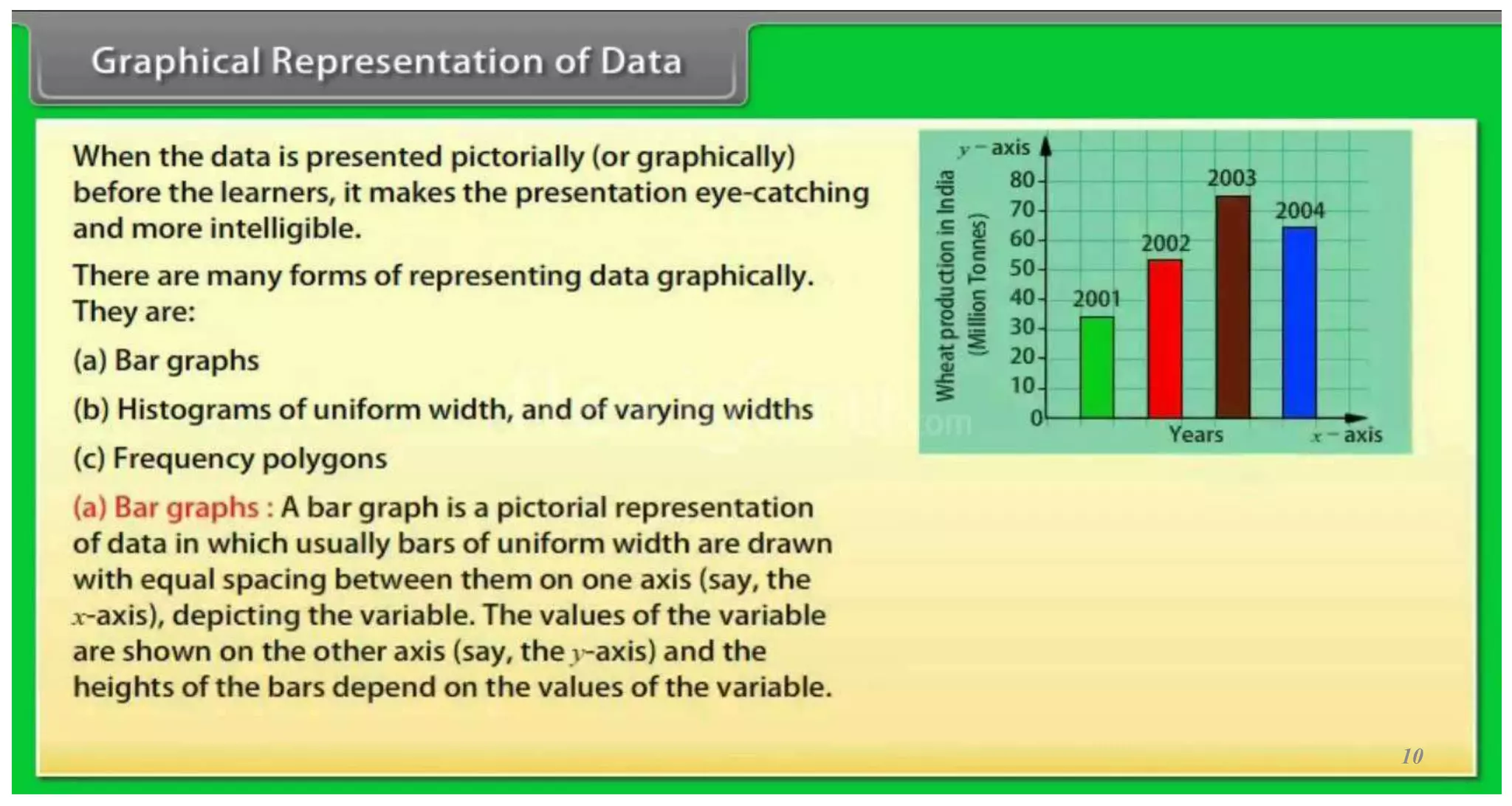
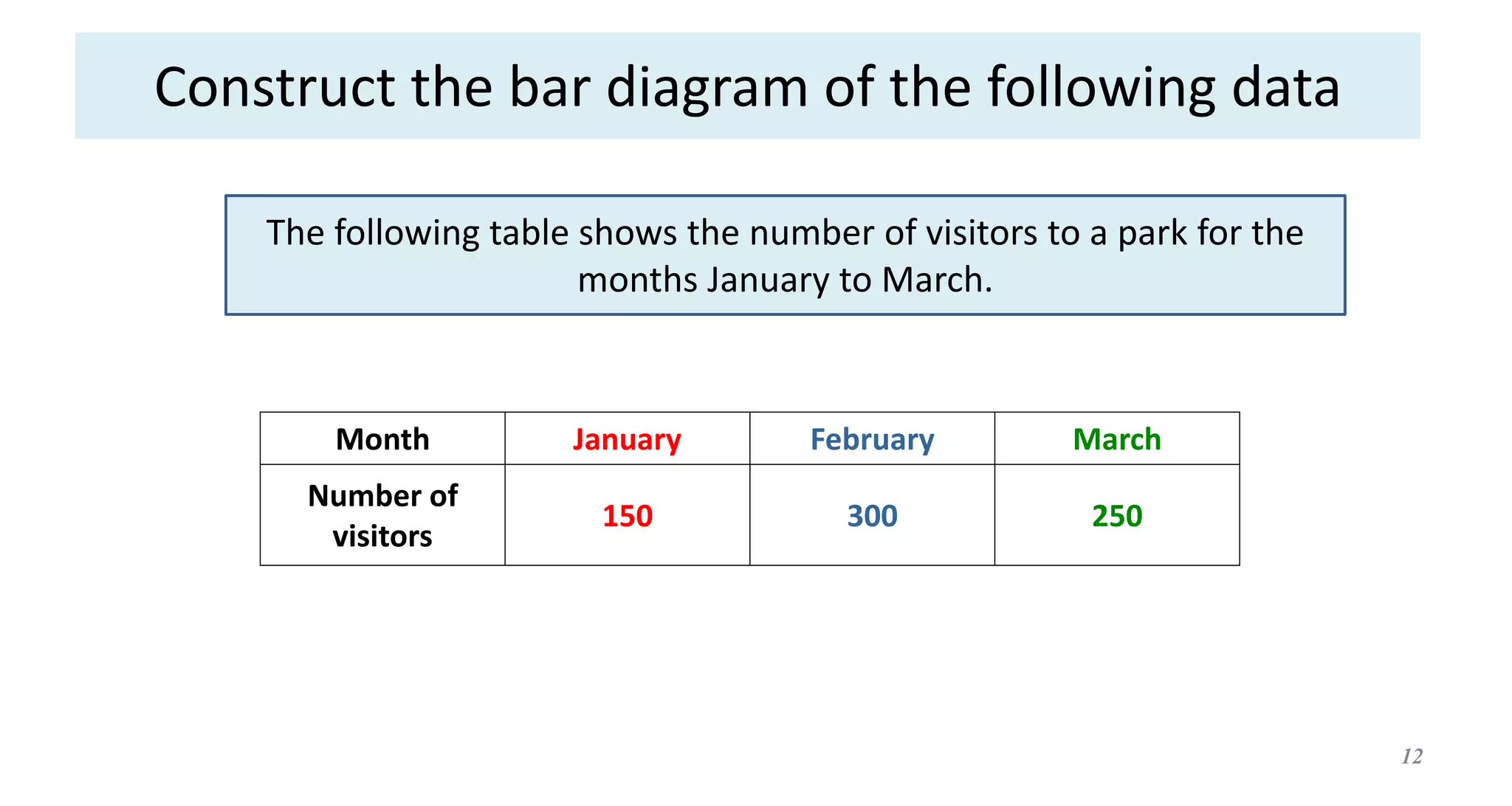
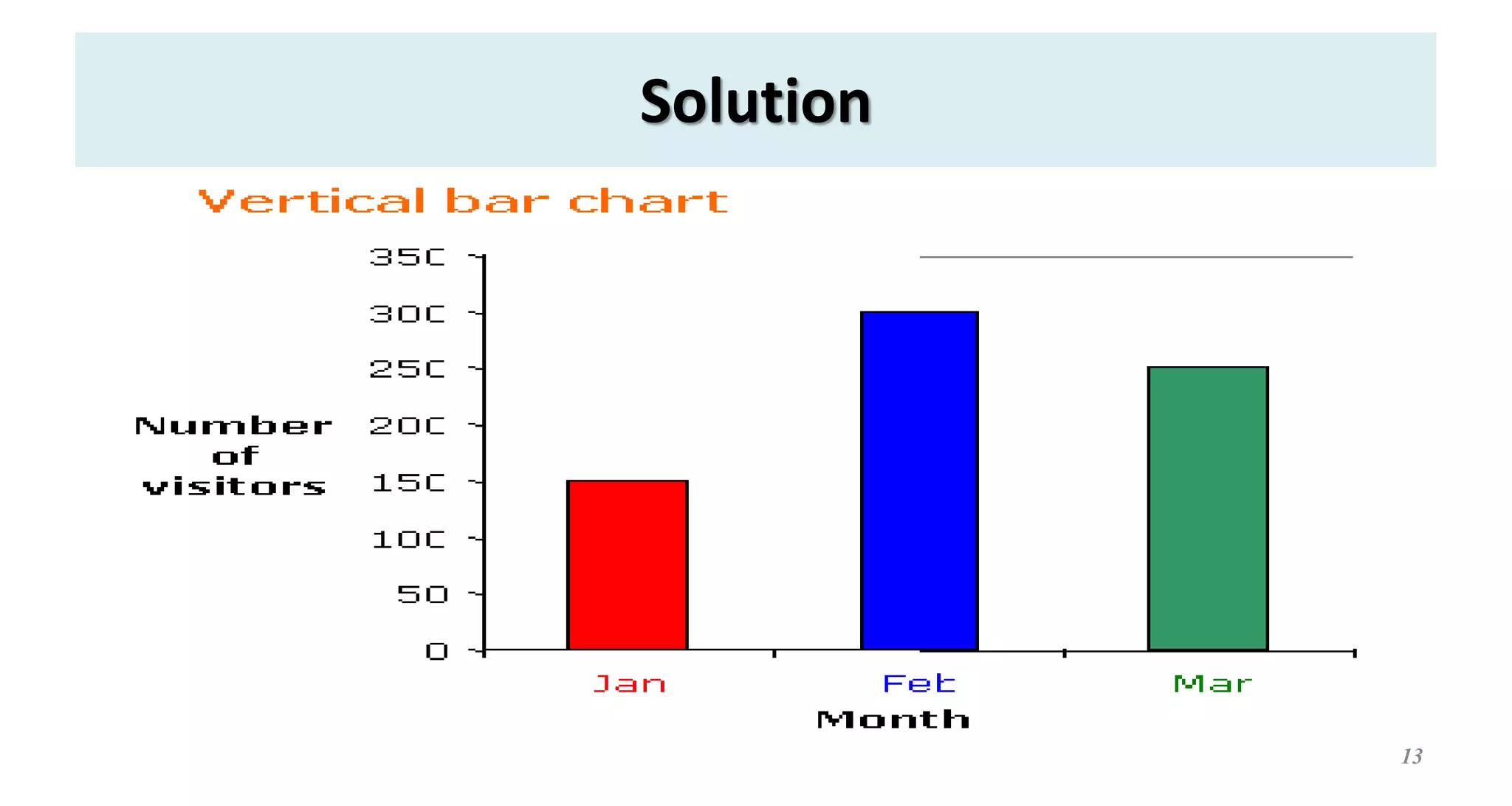
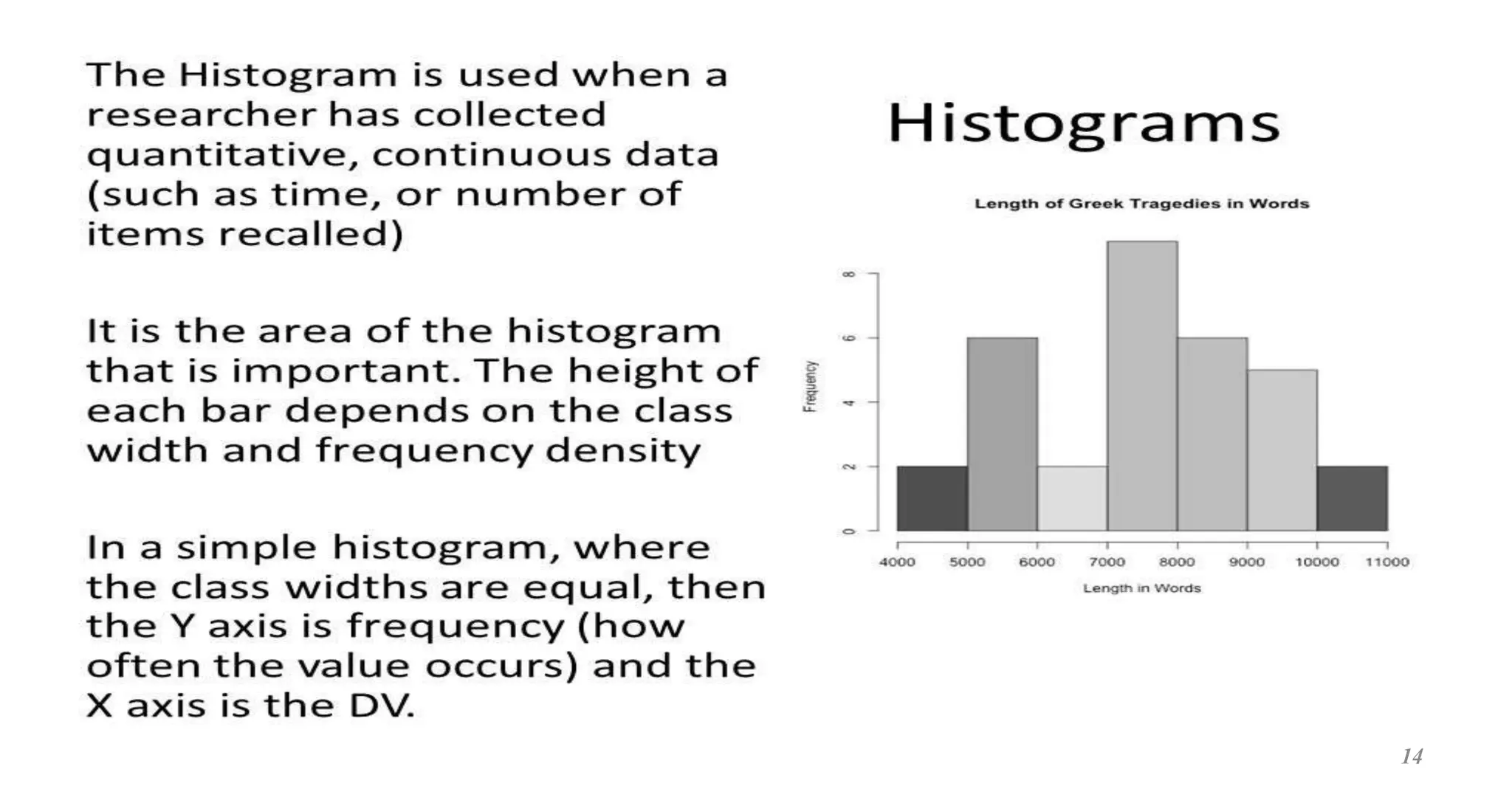
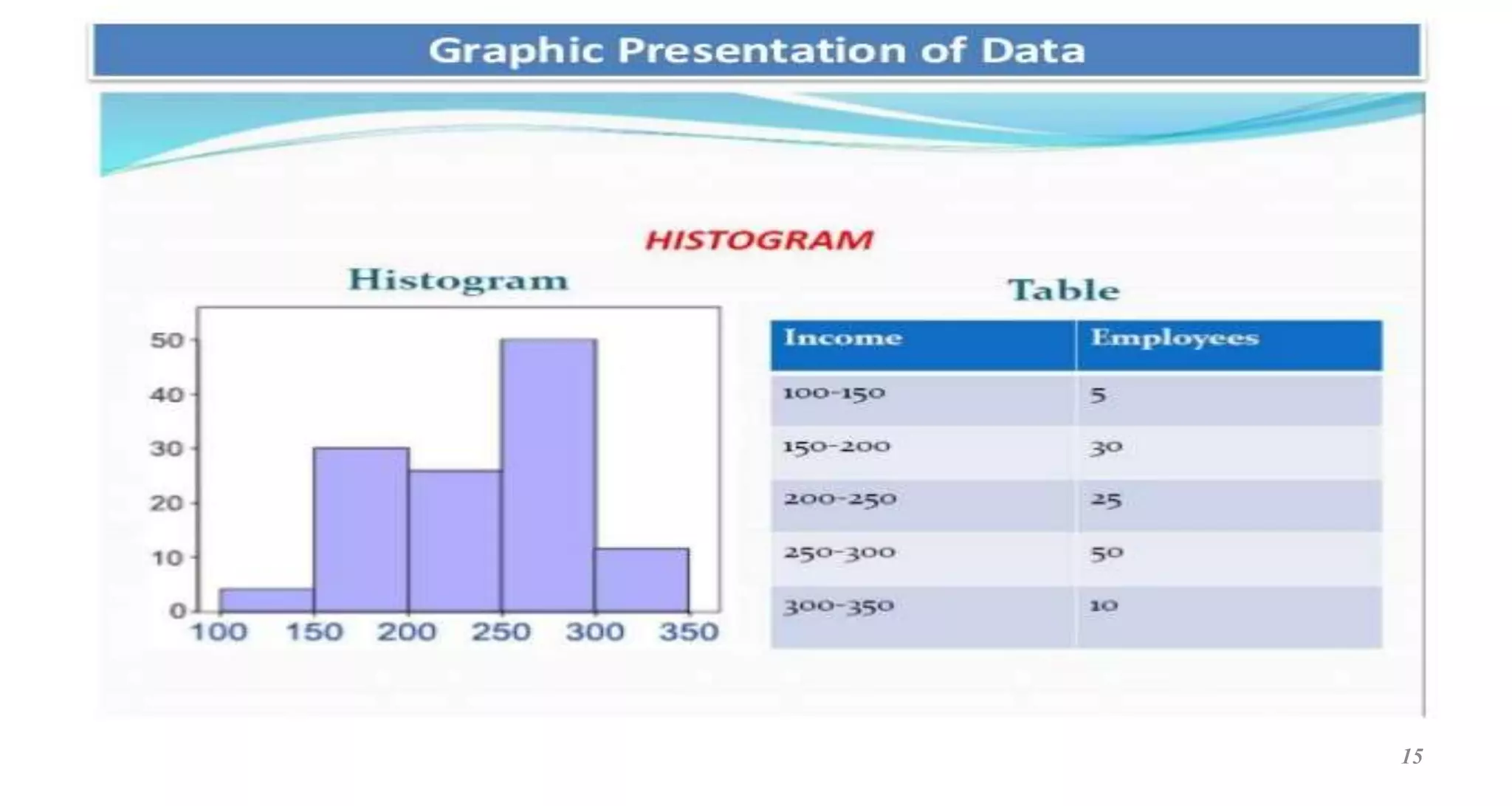
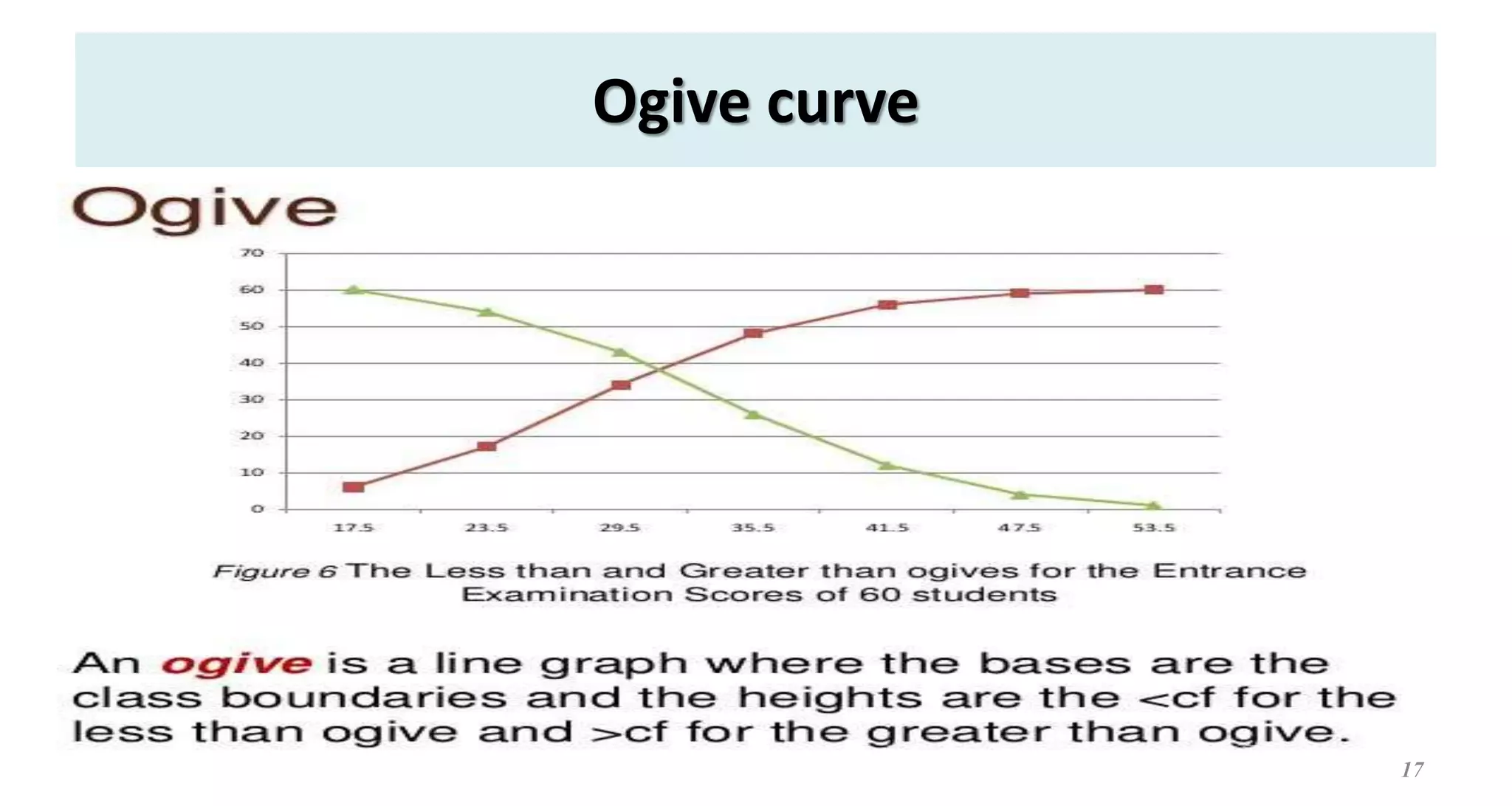
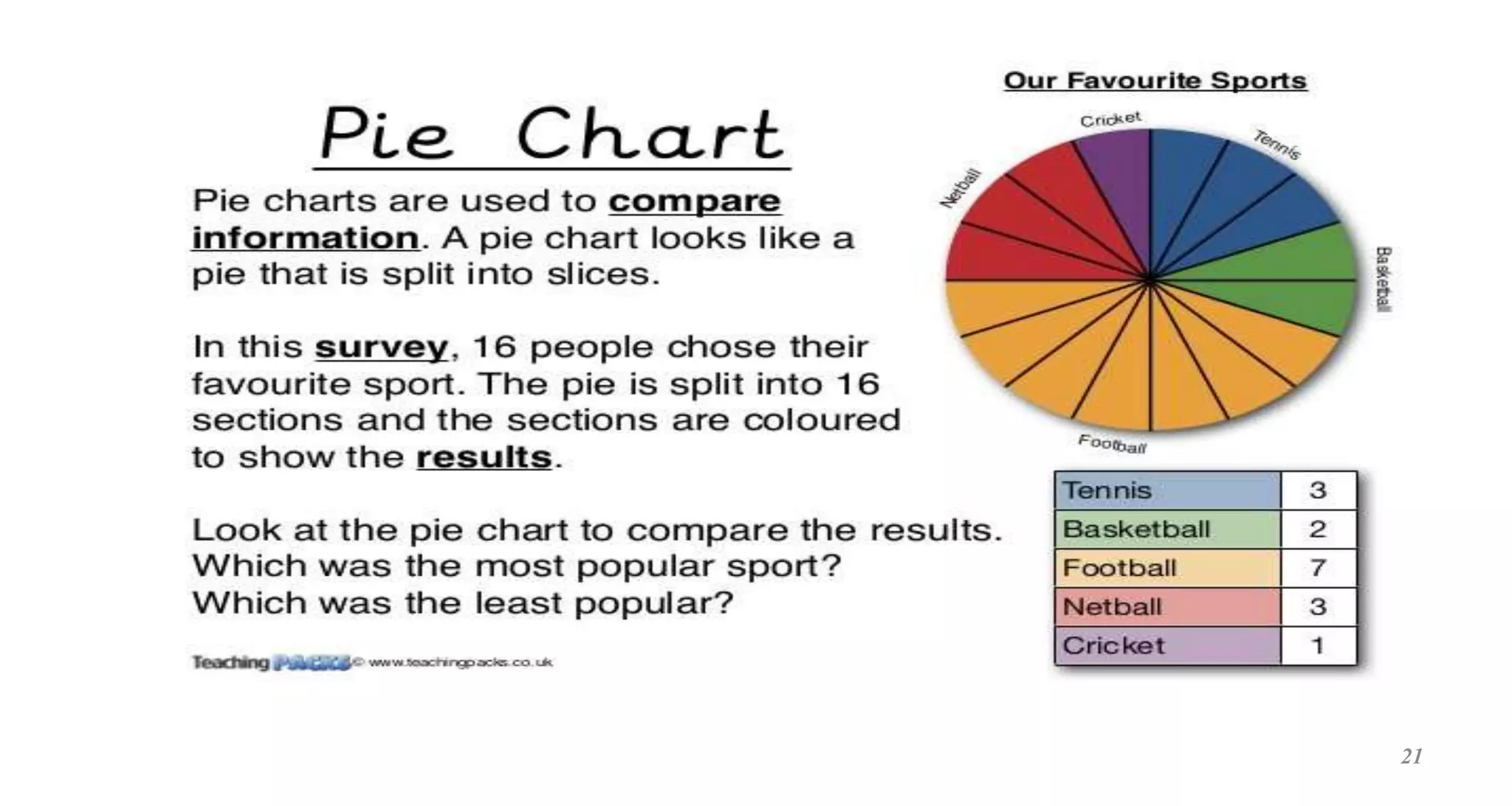
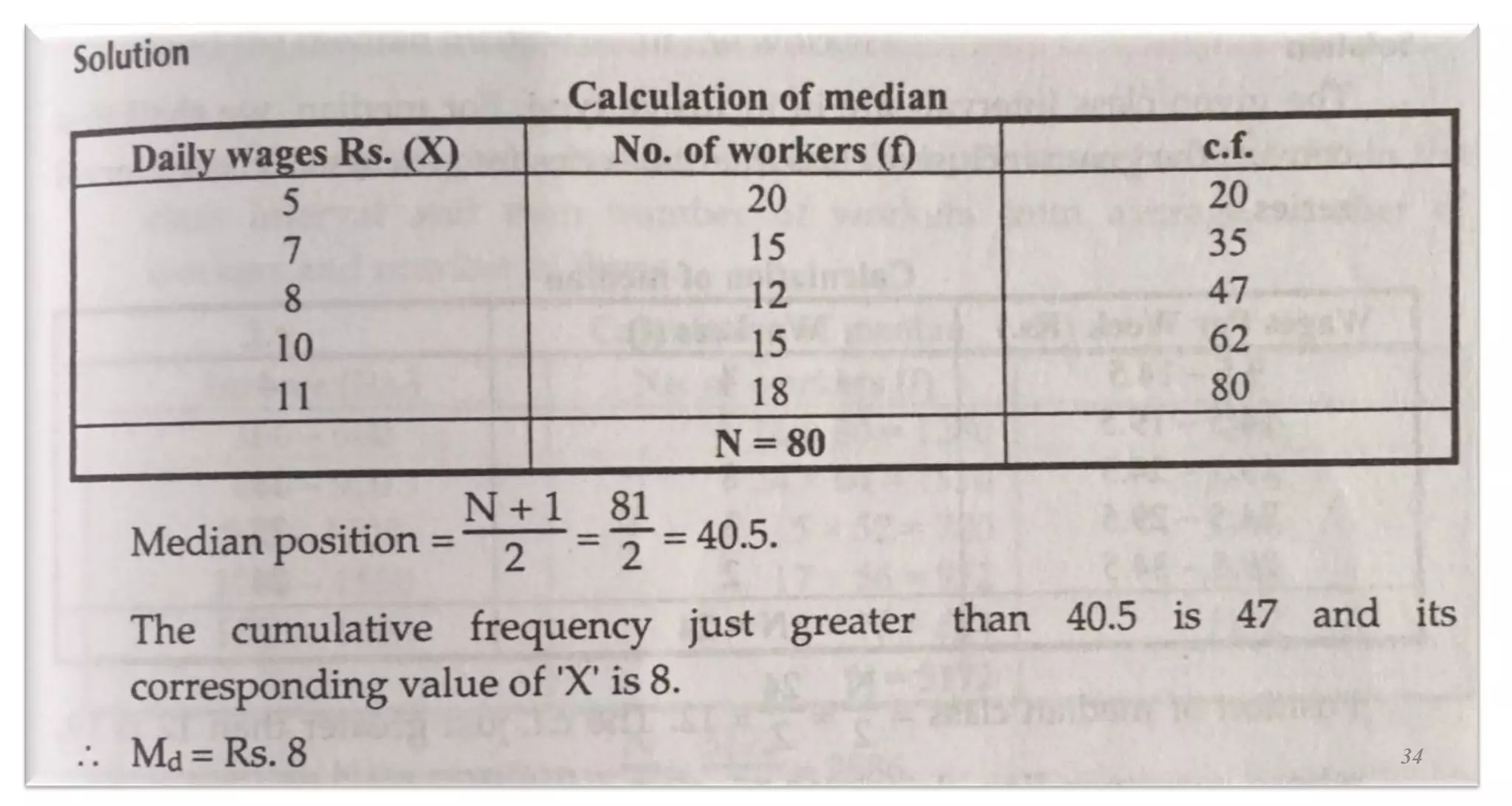
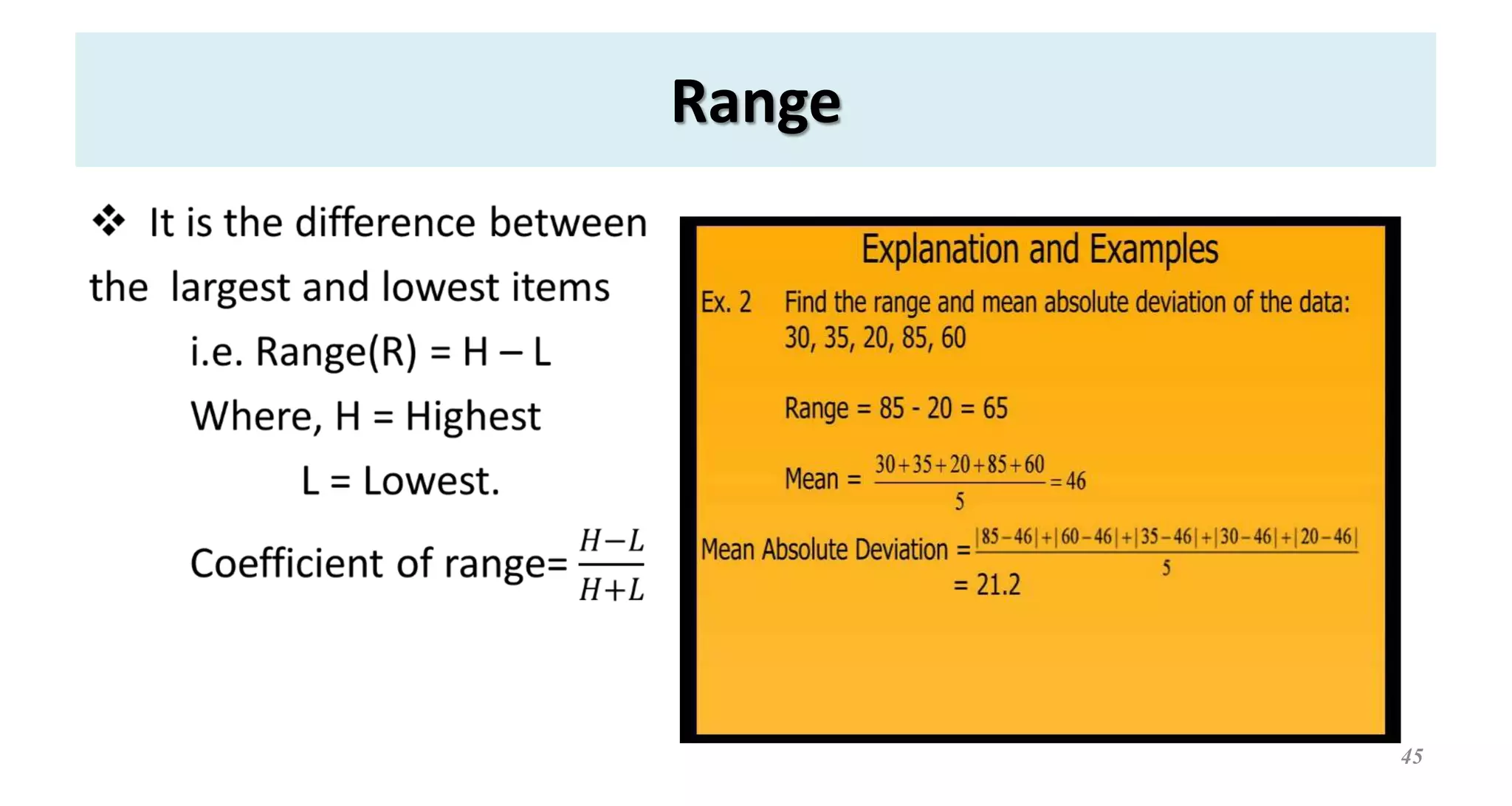
This document provides an overview of descriptive statistics concepts. It defines statistics, descriptive statistics, and inferential statistics. Descriptive statistics involves summarizing and describing data through measures of central tendency like mean, median, and mode, and measures of dispersion like range, standard deviation, and variance. The document discusses different types of data and averages. It also demonstrates how to calculate various descriptive statistics measures and construct graphs like bar diagrams and ogives using sample data.

1. Statistical Techniques BCS-040
Prepared by :Narayan
Thapa
Lecturer at Tribhuvan
University, Amrit Science
College(ASCOL)
Part time lecturer ICA
college 1
Descriptive Statistics

2. Introduction
 Statistics is the science of art of learning from data
 It is concerned with the collection of data, its subsequent description, and its
analysis, which often leads to the drawing of valid conclusions
 It may be defined as the collection, presentation, analysis and interpretation
of numerical data.
2

3. Descriptive statistics
 The part of statistics concerned with the description and summarization
of data is called descriptive statistics
 Descriptive statistics measures the measure of location, measure of
dispersion, measure of skewness, measure of kurtosis etc.
3

4. Inferential statistics
 The part of statistics concerned with the drawing of conclusion is called
inferential statistics
 In inferential statistics; samples are taken from the population in such a
way that the drawn sample can represent the entire population
4

5. Data
 Data are the raw materials
for final statistical conclusions
 It can either be quantitative
or qualitative or attributes
5

6. 6

7. Primary data
 The data which are originally collected by investigator or researcher
for the first time for the purpose of statistical enquiry is called primary
data
 It is collected by government, in individual, institution and research
bodies
 It needs more fund, time and manpower
 It is more reliable and suitable
7

8. Secondary data
 The data that has been already collected for a particular purpose and
used for next purpose is called secondary data
 It is not new and original data
 These types of data are generally published in newspapers,
magazines, bulletins, reports, journals, website, radio etc.
8

9. Population
 It is totality of units or items under study belonging to a particular a class
or group
 For example children in a school, patients in a hospital, fruits in a tree,
fishes in a pond etc.
 Population can be divided
into finite, infinite, homogeneous
population, heterogeneous
population
9

10. 10

11. 11

12. Construct the bar diagram of the following data
Month January February March
Number of
visitors
150 300 250
12
The following table shows the number of visitors to a park for the
months January to March.

13. Solution
13

14. 14

15. 15

16. 16

17. Ogive curve
17

18. Less than ogive curve
18

19. Less than or more than ogive
19

20. Calculation of median from ogive curve
20

21. 21

22. 22

23. Summarisation of data
 Summarization is a key data mining concept which involves techniques
for finding a compact description of a dataset.
 Some of the important measures are
a) Measure of central tendency
b) Measure of dispersion
23

24. Measure of central tendency
 The single value that represents the characteristic of the entire data.
Such a value is called the central value or an average
 The process of obtaining an average value from the entire data is
known as measure of central tendency
 It is designed to measure the concentration of the value in the central
part of the distribution
 It also enables us to compare two or more sets of data to facilitate
comparison
24

25. Types of average
25

26. Mean or Average
26
 Arithmetic mean is defined as the sum of all
observation is divided by the number of the
observation
 It is also called Arithmetic average

27. Calculation of Simple Arithmetic Mean
27

28. Calculate the Arithmetic mean of the following
 Income (Rs.): 1780, 1760, 1680, 1750, 1830, 1940, 1100, 1800, 1060,
1950
Variabes 15 20 25 30 40 45 49 50 54 55
Frequen
cy
2 5 6 7 1 3 4 6 1 1
Marks
obtained
10-20 20-30 30-40 40-50 50-60 60-70 70-80
No. of
students
4 5 7 10 12 6 3
28

29. Median
 The variate value dividing the total number of observation into two
equal parts is called Median
 The median divides the whole observation into two equal halves.
 It is the positional average
 It is denoted by Md
29

30. Calculation of median in individual series
30

31. Calculate the median from the following data
39, 38, 59,40, 67, 52, 77, 75, 24
391,384, 591, 407, 672, 522, 777, 753, 2488, 1490
31

32. Calculation of median in discrete series
32

33. Calculate the median from the following data
Daily
wages(Rs)
5 7 8 10 11
Number of
workers
20 15 12 15 18
33

34. 34

35. Calculation of median in continuous series
35

36. Cont…
36

37. Calculate the median from the following data
Wages per
week
10 - 14 15- 19 20 - 24 25 - 29 30 - 34
No of workers 4 7 8 3 4
37

38. Conversion of inclusive into exclusive class interval
 To convert the inclusive series into exclusive series ;
Correction factor = (15-14)/2=0.5
 This is added to the upper limit and subtracted from the lower limit of
the class. The exclusive class interval table is shown below
Wages per
week
9.5 – 14.5 14.5- 19.5 19.5 – 24.5 24.5 – 29.5 29.5- 34.5
No of workers 4 7 8 3 4
38

39. 39

40. Calculate the median from the following data
Height(in
cm)
161-167 167-173 173-179 179-185 185-191 191-197
No. of
students
79 92 60 22 5 2
Marks
obtained
Below 10 10-20 20-30 30-40 40-50 50 and
above
No. of
students
4 6 10 15 8 7
40

41. Mode
41

42. For asymmetrical distribution
42
For asymmetrical
distribution,
Mode=3Median-
2Mean
For the bimodal data
10,10,20,20,30,31,13

43. Measure of dispersion
 Dispersion means scatter or spread
or variation
 It is the descriptive statistical measure
which is used to measure the variation
or spread of the items from the central
value
43

44. Methods of studying dispersion
 Range
 Quartile deviation (or Semi-Inter Quartile Range)
 Standard deviation
 Mean deviation
 Coefficient of variation
44

45. Range
45

46. Quartile deviation
46

47. Standard deviation
47
Standard deviation is
defined as the positive
square root of the mean of
the squared deviations taken
from the mean. It is the
most important and widely
used measure of dispersion
or variability

48. Variance
48
The square of the
standard deviation is
known as variance

49. Coefficient of Variation (CV)
49