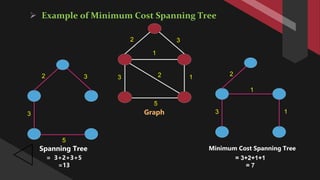
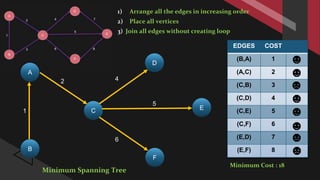
The document outlines Kruskal's algorithm, a greedy method for finding the minimum spanning tree in a connected weighted graph. It describes the necessary properties of spanning trees, the definition of minimum cost spanning trees, and provides a step-by-step algorithm along with its time complexity analysis. The algorithm's performance is characterized as O(e log v) or O(e log e), where e represents the number of edges and v the number of vertices.

1. Minimum
Spanning Tree
Using
Kruskal’s Algorithm

2. Name: Mrunal Patil
Year: First Year MCA
Design & Analysis
of Algorithm
Greedy Technique
Algorithm Design
Technique :
Problem : Kruskal’s Algorithm

3.  Greedy Method
• It is very straight forward algorithm design technique.
• A problem have ‘n’ inputs and we have to obtain subset of inputs that satisfies
some constraint.
• We need to find the feasible solution that either maximizes or minimizes
given objective function.
• A feasible solution, that optimize the solution is called optimal solution.

4.  Spanning Tree
Let G=(V,E) be an undirected connected graph.
A sub-graph t=(V, E’) is a spanning tree of G if and only if, t is tree.
• All vertices should be included
• No Loop should be created
𝑉1
𝑉2 𝑉3
𝑉4
𝐸1
𝐸2 𝐸4
𝐸3
Spanning Tree
Graph

5.  Minimum Cost Spanning Tree
• A minimum cost spanning tree is special kind of tree that minimizes
length of the tree.
• The cost of the spanning tree is the sum of the weights of all
the edges in the tree.
• Minimum spanning tree is the spanning tree where the cost is
minimum among all the spanning trees.

6. 2 3
3
5
2 3
3 1
2
1
5
2
3 1
1
Graph
Minimum Cost Spanning Tree
Spanning Tree
 Example of Minimum Cost Spanning Tree
= 3+2+3+5
=13
= 3+2+1+1
= 7

7. Kruskal’s Algorithms
Kruskal's algorithm is used to find the minimum spanning tree for a
connected weighted graph.
Kruskal's algorithm follows greedy approach which finds an optimum solution at
every stage instead of focusing on a global optimum.

8.  Algorithm

9.  Program

10. A
B
E
F
D
C
1
3
2
5
4
6
7
8
 Consider this graph

11. 3) Join all edges without creating loop
A
B
E
F
D
C
1
2
5
4
6
EDGES COST
(B,A) 1
(A,C) 2
(C,B) 3
(C,D) 4
(C,E) 5
(C,F) 6
(E,D) 7
(E,F) 8
1) Arrange all the edges in increasing order
2) Place all vertices
Minimum Spanning Tree
Minimum Cost : 18

12. Time complexity of Kruskal’s Algorithm
= O(ElogV) or O(ElogE)
Analysis-
•The edges are maintained as min heap.
•The next edge can be obtained in O(logE) time if graph has E edges.
•Reconstruction of heap takes O(E) time.
•So, Kruskal’s Algorithm takes O(ElogE) time.
•The value of E can be at most O(V2).
•So, O(logV) and O(logE) are same.
 Kruskal’s Algorithm Time Complexity-

13. Thank You