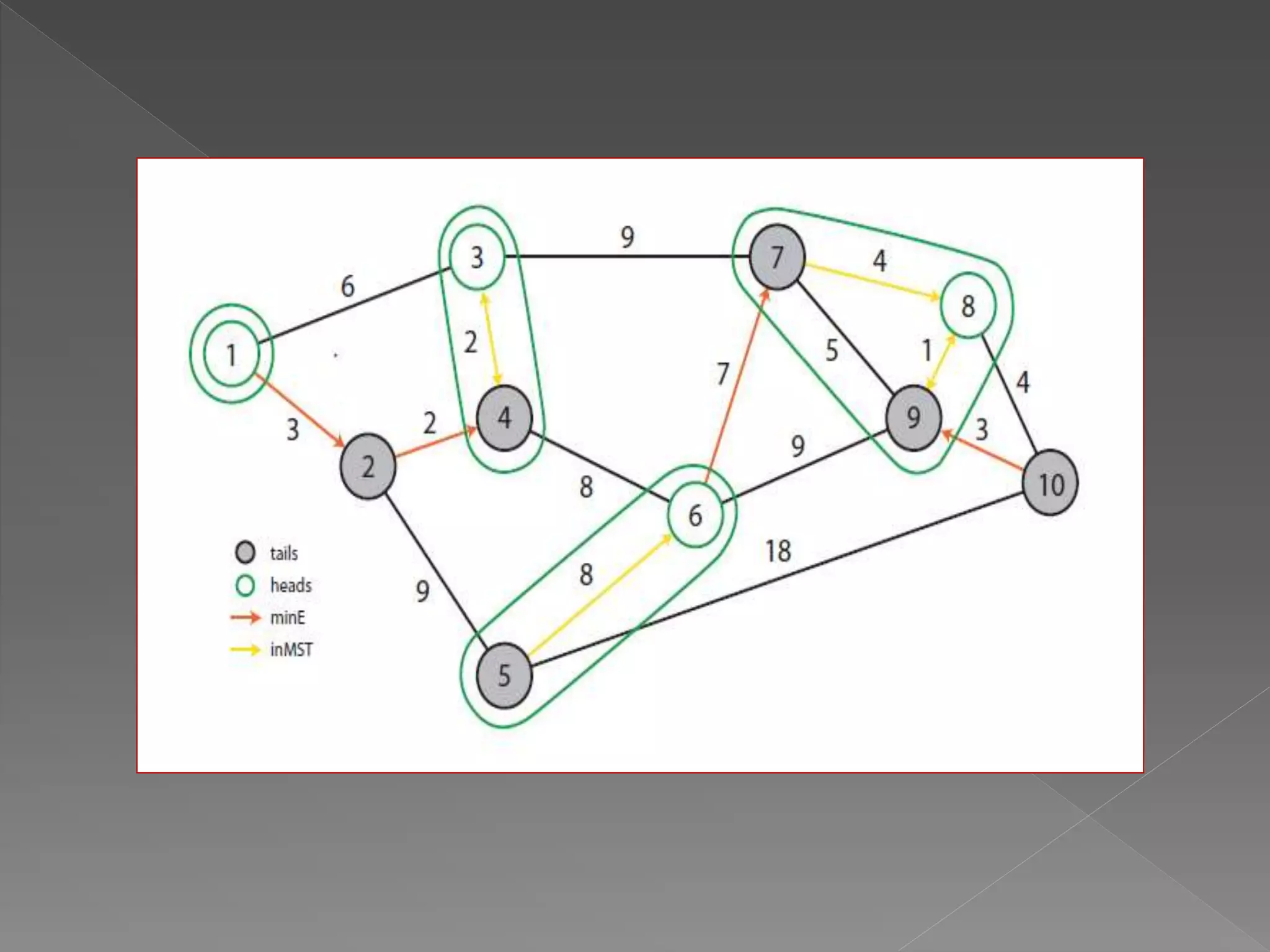
The document describes three algorithms for finding minimum cost spanning trees in graphs: Prim's algorithm, Kruskal's algorithm, and an optimal randomized algorithm. Prim's algorithm finds the minimum spanning tree by building the tree edge by edge in a greedy manner. Kruskal's algorithm finds the minimum spanning tree by adding edges in order of increasing weight, skipping edges that would create cycles. The randomized algorithm samples edges from the graph randomly and finds minimum spanning trees on the induced subgraph to eliminate edges that cannot be in the optimal solution.

1. Data Structure and Algorithm
Minimum Cost Spanning Tree
Submitted by,
M. Kavitha,
II – M.Sc(CS&IT),
Nadar Saraswathi College of
Arts & Science, Theni.

2. Data Structure and Algorithm
Contents :
1. Minimum Cost Spanning Tree
1.1. Prim’s Algorithm
1.2. Kruskal’s Algorithm
1.3. An Optimal Randomized Algorithm (*)

3. Minimum – Cost Spanning Tree
Definition :
* Let G = (V,E) be an undirected connected graph.
* A sub-graph t = (V,E’) of G is a spanning tree of
G iff t is a tree.
1
2
376
5 4
10
28
14 16
24
25
22
18 12
1
2
376
5
4
10
14 16
25
22
12
Fig 1 : Graph and minimum – cost spanning tree

4. Prim’s Algorithm
* A greedy method to obtain a minimum-cost spanning
tree builds the tree edge by edge.
* Prim's algorithm finds a minimum spanning tree
(MST) for a connected weighted graph.
* MST = subset of edges that forms a tree including
every vertex, such that total weight of all edges is minimum cost
spanning.
There are two possible ways:
1. The set of edges so far selected form a tree. If A is the set
of edges selected so far then A forms a tree.
2. The next edge (u,v) to be include in A is a minimum-cost
edge not in A with the property that AU{(u,v)} is also a tree.

5. 1
2
376
5
4
1
2
376
5
4
10
25
10
(A) (B)
1
2
376
5
4
10
25
22
(C)
Stages in Prim’s Algorithm :

6. 1
2
376
5
4
10
25
22
12
1
2
376
5
4
10
16
25
22
12
1
2
376
5
4
10
14 16
25
22
12
(D) (E)
(F)

7. * The algorithm is a minimum cost spanning tree
includes for each vertex v a minimum-cost edge incident to v.
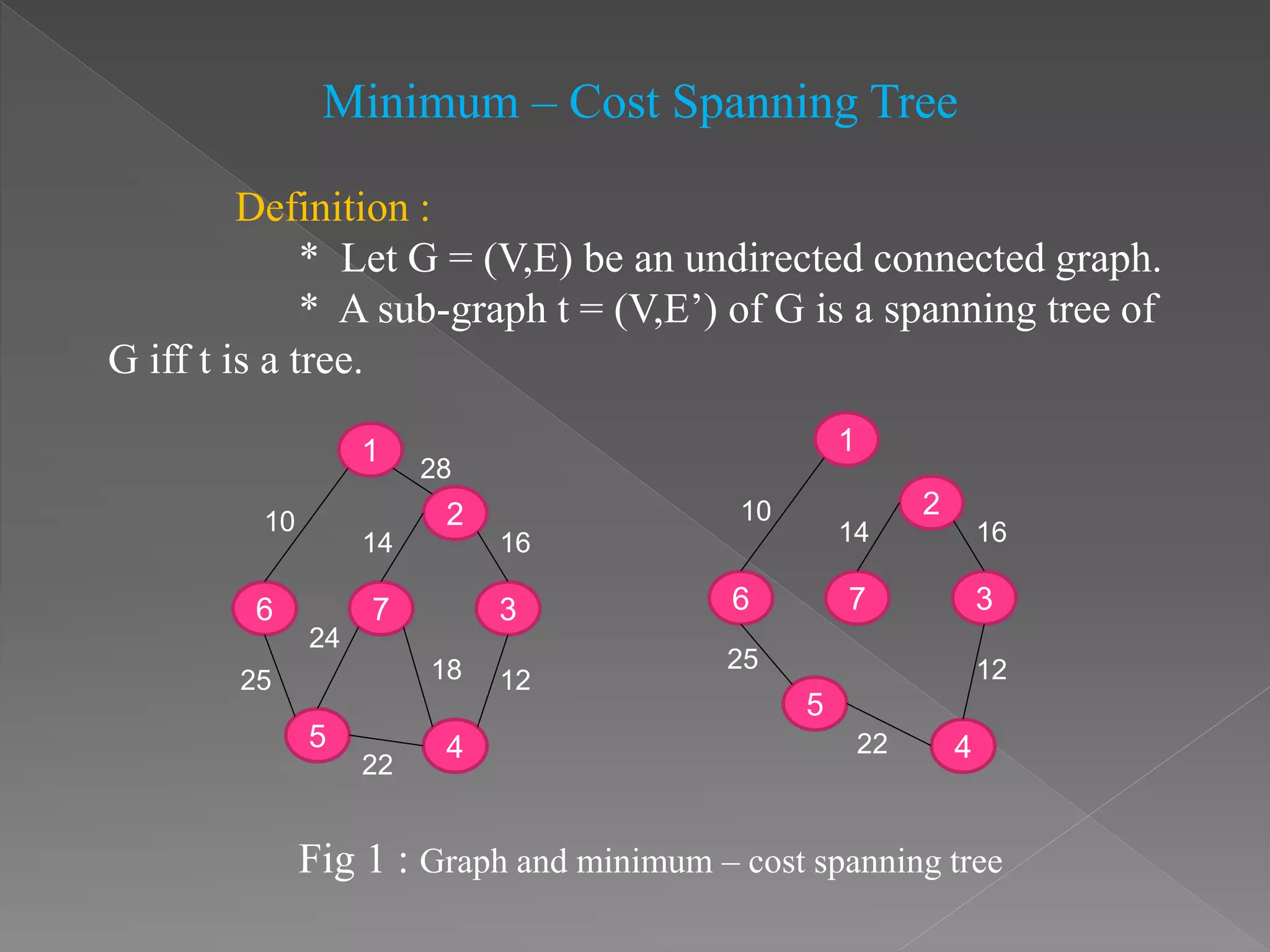
* It support t is a minimum-cost spanning tree for G =
(V,E).
* These algorithms find the minimum spanning forest
in a possibly disconnected graph.
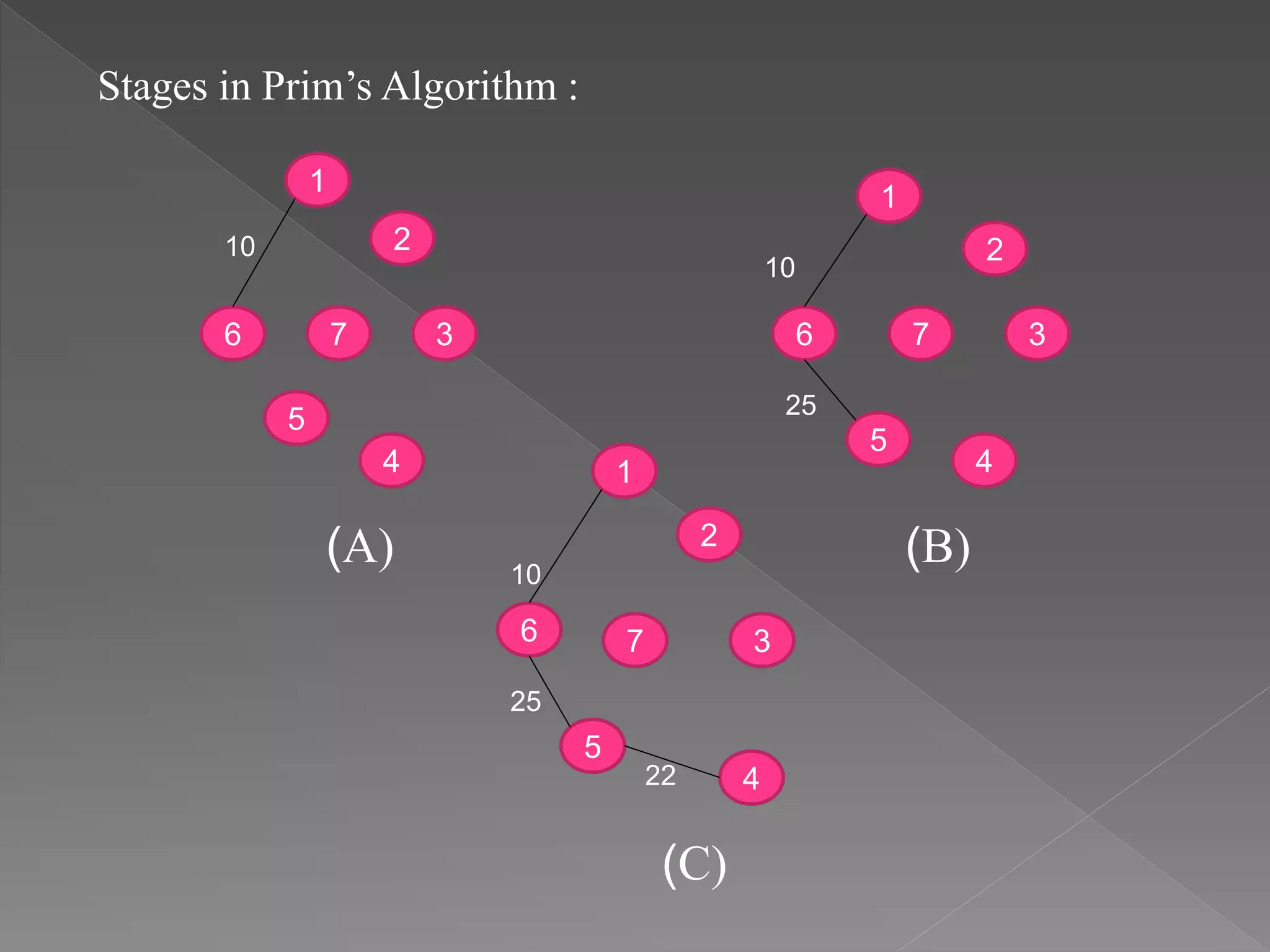
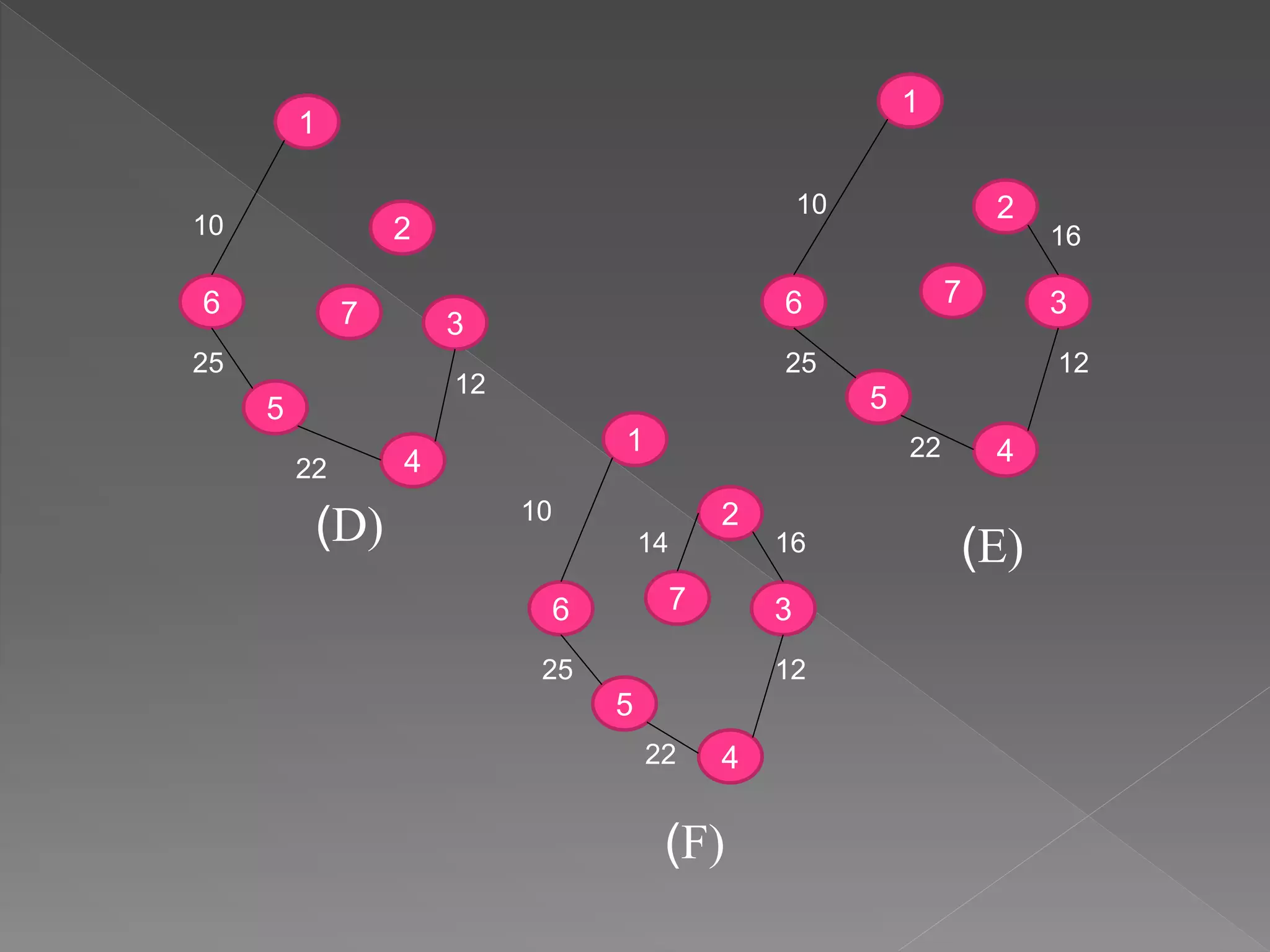
* The most basic form of Prim's algorithm only finds
minimum spanning trees in connected graphs.
mincost :=0;
for i:=2 to n do near[i]:=1;
// Vertex 1 is initially in t.
near[i]:=0;
for i:=1 to n-1 do
{
// Find n-1 edges for t.

8. Algorithm Prim(E,cost,n,t)
{
Let(k,l) be an edge of minimum cost in E;
mincost:=cost[k,l];
t[1,1]:=k; t[1,2]:=l;
for i:=1 to n do
if (cost[i,l]<cost[i,k])then near[i]:=l;
Else near[i]:=k;
near[k]:=near[l]:=0;
for i:=2 to n-1 do {
Let j be an index such that near[j]≠0 and
cost[j,near[j]] is minimum;
t[i,1]:=j;t[i,2]:=near[j];
mincost:=mincost+cost[j,near[j]];
near[j]:=0;
for k:=1 to n do
if((near[k]≠0)and(cost[k,near[k]]>cost[k,j]))
then near[k]:=j; }
return mincost;
}
Prim’s minimum-cost
spanning tree algorithm

9. kruskal’s Algorithm
* Kruskal's algorithm is a greedy algorithm in graph
theory that finds a minimum spanning tree for a connected
weighted graph.
* This means it finds a subset of the edges that forms
a tree that includes every vertex, where the total weight of all
the edges in the tree is minimized.
* If the graph is not connected, then it finds a
minimum spanning forest (a minimum spanning tree for each
connected component).
* Kruskal's Algorithm add edges in increasing weight,
skipping those whose addition would create a cycle.

10. 1
2
376
5
4
1
2
376
5
4
10
1
2
376
5
4
10
12
(A)
(c)
(B)
Stages in Kruskal’s Algorithm :

11. 1
2
37
6
5
4
1
2
376
5
4
10
1
2
376
5
4
10
12
(D)
(F)
(E)
10
12
14
14 16
12
14 16
22

12. t:=0;
while (t has less than n-1 edges) and (E≠0)) do
{
Choose an edge(v,w) from E of lowest cost;
Delete (v,w) from E;
if (v,w) does not create a cycle in t then add (v,w) to t;
else discard (v,w);
}
1.Would create a cycle if v and w are already in the
same component.
2. I We start with a component for each node.
3. I Components merge when we add an edge.
4. Need a way to: check if v and w are in same
component and to merge two components into one.

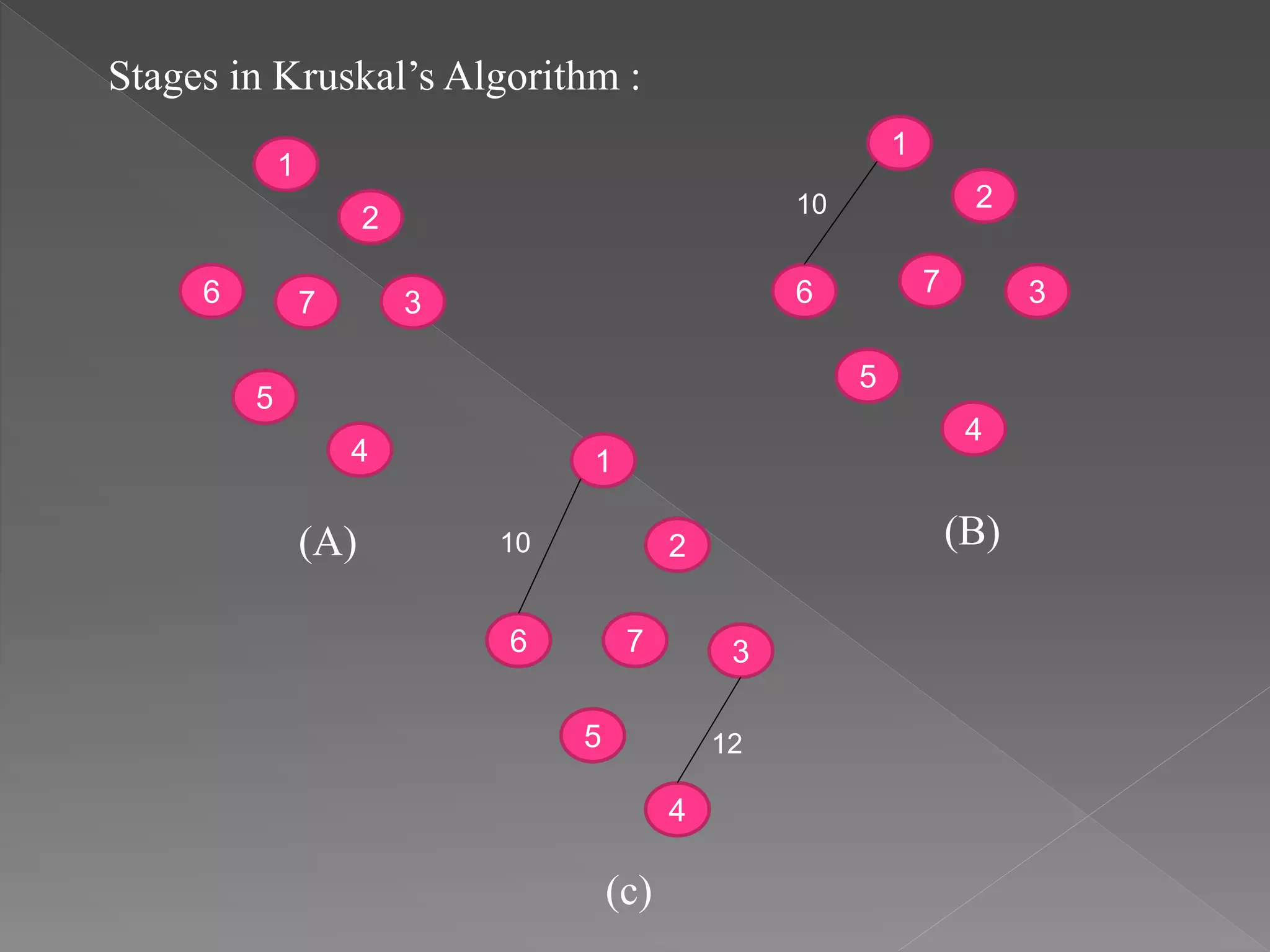
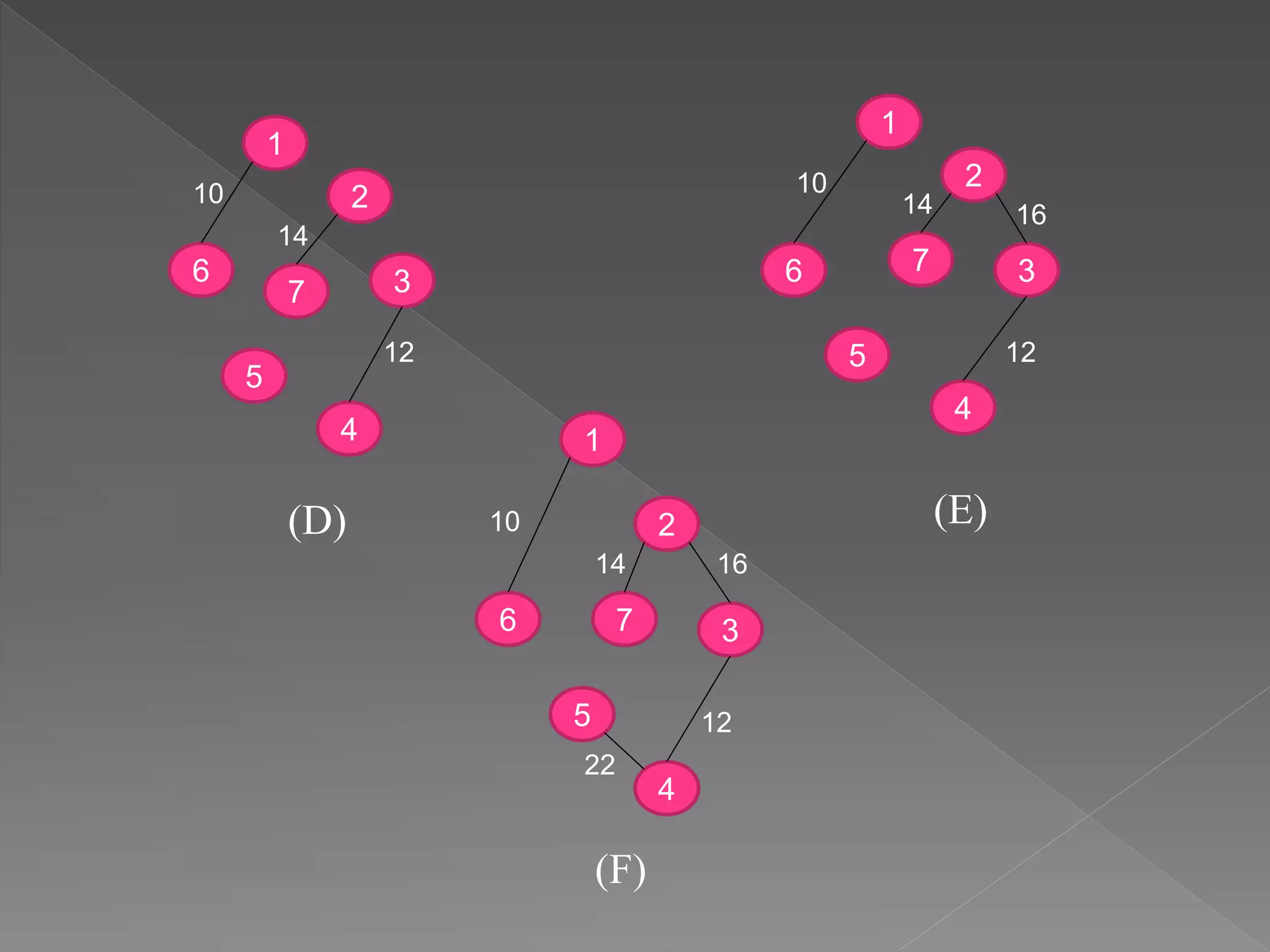
13. Algorithm Kruskal(E,cost,n,t)
{
Construct a heap out of the edge costs using
Heapify;
for i:=1 to n do parent[i]:=-1;
i:=0; mincost:=0.0;
While((i<n-1) and (heap not empty)) do {
Delete a minimum cost edge (u,v) from the
heap and reheapify using Adjust;
j:=Find(u);k:=Find(v);
if(j≠k) then {
i:=i+1;
t[i,1]:=u;t[i,2]:=v;
mincost:=mincost+cost[u,v];
Union(j,k);
} }
if(i≠n-1) then write(“No spanning tree”);
else return mincost;
}
Kruskal’s Algorithm

14. An Optimal Randomized Algorithm (*)
* The minimum-cost spanning tree of a graph G(V,E) to
spend Ω(|V|+|E|) time in worst case.
* A randomized algorithm that runs in time the
Õ(|V|+|E|) can be devised :
1. Randomly sample m edges from G (for some suitable m).
2. Let G’ be the induced sub graph that is G’ has V as its
node set and the sampled edges in its edge set.
3. The sub graph G’ need not be connected a minimum-cost
spanning tree for each component of G;.
4. Let F be the minimum-cost spanning tree forest of G’.
5. F eliminate edges called the F-heavy edges of G that
cannot possibly be in a minimum-cost spanning tree.

16. Thank You