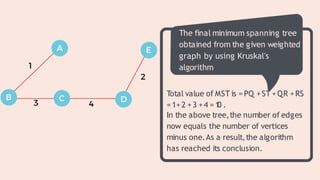
Kruskal's algorithm is designed to find the minimum spanning tree of a connected weighted graph using a greedy approach that optimizes edge selection at each step. The algorithm involves sorting edges by weight, adding them to the spanning tree while ensuring no cycles are formed, until all vertices are connected. Its applications include building electrical wiring and establishing LAN connections.

1. KRUSKAL ALGORITHM
By Group 12

2. Kruskal's Algorithm is used to find the minimum spanning tree for a
connected weighted graph. The main target of the algorithm is to find
the subset of edges by using which we can traverse every vertex of the
graph. It follows the greedy approach that finds an optimum solution at
every stage instead of focusing on a global optimum.
# About Kruskal’s Algorithm

3. Spanning tree - A spanning tree is the subgraph of an undirected
connected graph.
Minimum Spanning tree - Minimum spanning tree can be defined as
the spanning tree in which the sum of the weights of the edge is
minimum. The weight of the spanning tree is the sum of the weights
given to the edges of the spanning tree.
Some Basic Terms Before Starting:

4. InKruskal's algorithm,westart fromedgeswiththelowest
weightandkeepaddingtheedgesuntilthegoalis reached.
Thesteps to implementKruskal's algorithmarelisted as
follows -
First, sort alltheedgesfromlowweighttohigh.
Now
,take the edgewith the lowest weight andaddit
tothespanningtree.If theedgetobeaddedcreatesa
cycle,thenreject theedge.
Continuetoaddtheedges untilwereachallvertices,
anda minimumspanningtreeis created.
Exampleof Kruskal’
s A
lgorithm
How Does Kruskal’s
Algorithm works? Let’
s lookat howKruskal’
s approach functions
using anexample.Using anexample,it willbe
easier to comprehendKruskal’
s algorithm.
Let’
s assumeaweightedgraphis –

5. 1.) Table after organizing the edges in the ascending
order according to their weights :-
Edge AB DE BC CD AE AC AD
Weight 1 2 3 4 5 7 10

6. Phase 1– J
oin the edge PQ
having the weight 1to the
MST.
Phase 2 – J
oin the edge ST
having the weight 2 to the
MST
.Also,point to be
noted that this is not
making any cycle.

7. Phase 3 –Add the edge
QR having the weight 3
to the MST
Phase 4 – Select the edge
RS having the weight 4 to
the MST;also,you will
notice that it is not
composing the cycle

8. Phase 5 –Now, we will select the edge PT having the weight 5.
Adding this edge will form the cycle, so we will dump it.
Phase 6 –Pick the edge PR having the weight 7.Adding this edge
will form the cycle,so we will dump it.
Phase 7–Pick the edge PS having the weight 10.Adding this edge
will form the cycle,so we will dump it.

9. Total value of MST is =PQ +ST +QR +RS
=1+2 +3 +4 =1
0 .
In the above tree,the number of edges
now equals the number of vertices
minus one.As a result,the algorithm
has reached its conclusion.
The final minimum spanning tree
obtained from the given weighted
graph by using Kruskal's
algorithm

10. THE APPLICATIONS OF KRUSKAL’S
ALGORITHM
The technique by Kruskal can be used to build out
electrical wiring across cities.
It’s possible to operate it to set up LAN connections.

11. Group Members:
• Shashwat Mishra 23BAI10448
• Dev Marwah 23BAI10310
• Dhanni Watti 23BCY10343
• Prateek Chhabra 23BAI10169
• Rajrup Roy Choudhury 23BAI10213
• Aryan Desai 23BAI10179

12. THANK YOU