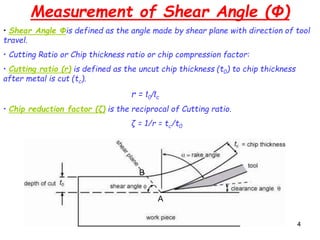
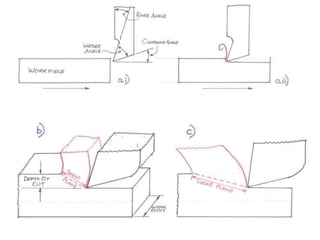
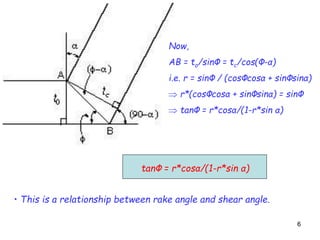
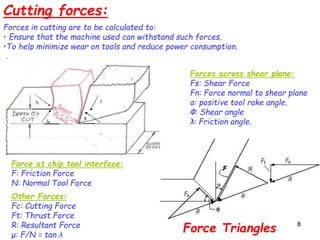
This document discusses the analysis of cutting forces in 2D orthogonal metal cutting using Merchant's circle theory. It introduces the mechanics of chip formation where a wedge-shaped tool shears metal along the primary shear plane at an angle (φ). Merchant's circle relates the shear angle (φ), rake angle (α), and friction angle (λ) and can be used to calculate cutting and thrust forces. The maximum shear stress theory states that the shear angle is selected to minimize the energy of cutting and is calculated based on α, λ, and an assumption that the material behaves plastically. Key cutting force relationships and assumptions of Merchant's model are also outlined.

1. 11
Topic – Analysis of Cutting forces in Orthogonal metal
cutting(2D cutting) with the help of Merchants Circle
by
Mr. Binit kumar
Assistant Prof., ME department
GLBITM, Greater Noida

2. 2
Introduction
• Object of mfg process is to produce piece of specified shape.
• Any of the following three type of operations may be employed for the same:
1. Constant Mass Operation (Casting, rolling etc.)
2. Material Addition Operation (Welding, Bolting, riveting etc)
3. Material Removal Operation (Machining, grinding, lapping etc)

3. 33
Mechanics of chip formation:
• Wedge shape tool is moved relative to work piece.
• Tool exerts pressure on work piece as it makes contact with the same causing
compression of metal near tool tip.
• Shear type plastic deformation within metal starts.
• Metal starts moving upwards along the top face of the tool.
• Tool advances and material ahead is sheared continuously along shear plane
(Primary shear zone).
• Tool surface along which chip moves upwards is called rake surface.
• Tool surface which is helps in avoiding rubbing with machined surface is called
flank surface.

4. 44
Measurement of Shear Angle (Φ)
• Shear Angle Φis defined as the angle made by shear plane with direction of tool
travel.
• Cutting Ratio or Chip thickness ratio or chip compression factor:
• Cutting ratio (r) is defined as the uncut chip thickness (t0) to chip thickness
after metal is cut (tc).
r = t0/tc
• Chip reduction factor (ζ) is the reciprocal of Cutting ratio.
ζ = 1/r = tc/t0
A
B

5. 55

6. 66
tanΦ = r*cosα/(1-r*sin α)
Now,
AB = to/sinΦ = tc/cos(Φ-α)
i.e. r = sinΦ / (cosΦcosα + sinΦsinα)
 r*(cosΦcosα + sinΦsinα) = sinΦ
 tanΦ = r*cosα/(1-r*sin α)
• This is a relationship between rake angle and shear angle.

7. 77
•Now if the length of cut ‘lo’ is known, then as per continuity
equation:
ρlobt = ρlcbtc
Where,
• ρ is the density of the material and material is assumed to be
incompressible.
• lc is the length of the chip.
lc/lo = to/tc = r
• Thus relation b/w rake angle and shear angle can be
redefined.

8. 88
Cutting forces:
Forces in cutting are to be calculated to:
• Ensure that the machine used can withstand such forces.
•To help minimize wear on tools and reduce power consumption.
Forces across shear plane:
Fs: Shear Force
Fn: Force normal to shear plane
α: positive tool rake angle.
Φ: Shear angle
λ: Friction angle.
Force at chip tool interface:
F: Friction Force
N: Normal Tool Force
Other Forces:
Fc: Cutting Force
Ft: Thrust Force
R: Resultant Force
μ: F/N = tan λ
Force Triangles

9. 99
• Shear Force ‘Fs’ is resistance to shear of metal.
• Normal Force ‘Fn’ is the force that w/p provides for backing up.
• Fs and Fn are at right angle to each other.
• R’ is the resultant of Fs and Fn and equal and opposite to R which is the resultant
of F and N. Thus R’ and R can be used interchangeably.
• Normal Tool Force ‘N’ acts at tool chip interface and is provided by the tool.
• Frictional Force ‘F’ is the frictional resistance of the tool acting on chip.
• All these forces can be represented with a circle called Merchant Force Circle.
• On this circle force triangles are superimposed.
• R or R’ forms the diameter of this circle.
Merchant Force Circle
• Orthogonal components of R, cutting
force Fc (horizontal) and thrust force Ft
(vertical) can be measure with the help of
dynamometer.
• Power consumed during cutting ‘E’ is:
E = Fc*V
• Where V is cutting speed.
• Now:
VV
F = Fc*Sinα + Ft*Cosα
N = Fc*Cosα – Ft*Sinα
And
Fs = Fc*CosΦ – Ft*SinΦ
Fn = Fc*SinΦ + Ft*CosΦ
V

10. 1010
Now,
Shear Plane Area ‘As’ is
As = bto/sinΦ
And average stresses on shear plane area are:
Τs = Fs/As
σs = Fn/As
Also from Merchant Force Circle:
Also;
R = Fc*sec(λ-α)
Thus, Fs = Fc*sec(λ-α)*Cos(Φ+λ-α)
Since, Τs = Fs*SinΦ/bto
Thus, Τs = Fc*sec(λ-α)*Cos(Φ+λ-α)*SinΦ/bto
Now ‘α’ for a tool is constant and assuming that ‘λ’ is independent of ‘Φ’, and for
Maximum shear stress:
dΤs/dΦ = 0
Cos(Φ+λ-α)*CosΦ - Sin(Φ+λ-α)*SinΦ
Fs = R*Cos(Φ+λ-α)
and
Fc = R*Cos(λ-α)

11. 11
Now,
Cutting Power Pc:
Pc = Fc*V
V = ΠDN/(1000*60) in m/s
Thus,
Pc = Fc*V/1000 in Kw
tan(Φ+λ-α) = cotΦ = tan(900-Φ)
• Thus on having high value of shear angle for a tool, value of friction angle reduces
• Thus low friction b/w tool and chip occurs and thus tool life increases and cutting
force required decreases.
Assumptions made by Merchant in making shear angle prediction:
• The work material behaves like an ideal plastic.
• The theory involves the minimum energy principle.
• As, Τs and λ are assumed to be constant and independent of Φ.
Φ = 450 + α/2 – λ/2

12. Thank you
12