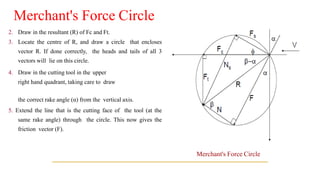
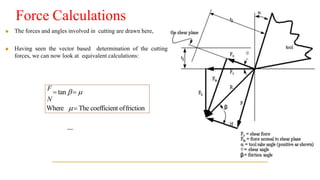
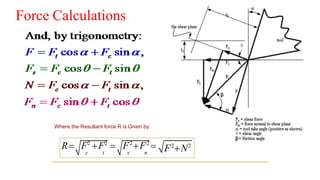
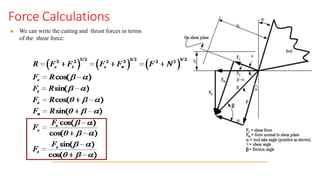
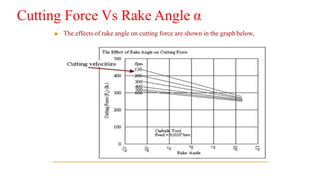
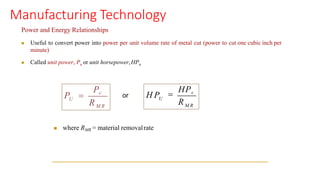
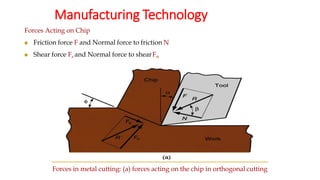
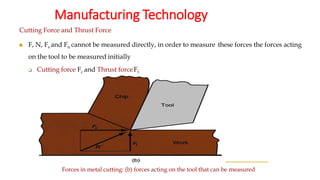
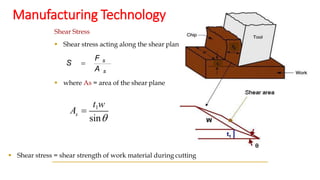
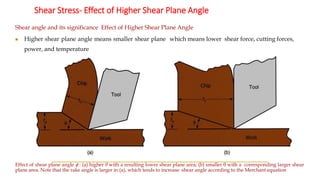
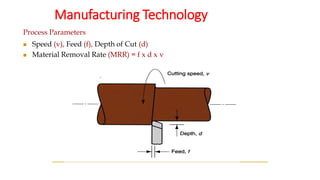
The document describes Merchant's Force Circle method for calculating forces in metal cutting. It involves drawing vectors representing cutting force, thrust force, resultant force, friction force, normal force, and shear force on a circle. The positions of the vectors' heads and tails on the circle allow calculation of these forces and their angles. The method can be used to determine power requirements and optimize cutting conditions like rake angle to minimize forces and temperature.