This document provides information about calculating the mean, variance, and standard deviation of a discrete probability distribution. It defines these key terms and provides the relevant formulas. Two examples are worked through, calculating these values for given probability distributions. In the first example, the mean is 5.45, variance is 1.95, and standard deviation is 1.40. In the second example, the mean is 10.5, variance is 57.25, and standard deviation is 7.57. The document concludes with an activity asking students to answer problems calculating these values.

1. Schedule:
Asynchronous- Tuesday (4:15-5:00 pm)
Synchronous- Thursday (4:15-5:00 pm)

2. MEAN, VARIANCE AND
STANDARD DEVIATION OF A
DISCRETE PROBABILITY
DISTRIBUTION
TCHR. JAKE GAD

3. Objective:
•Ability to compute for the MEAN.
•Ability to compute for the VARIANCE
and it’s function.
•Ability to compute for the STANDARD
VARIATION and it’s function.

4. DEFINITION OF TERMS
1.Mean (𝜇)
2.Variance(𝜎2)
3.Standard Deviation(𝜎)

5. MEAN (𝜇)
•Is the average of given numbers.
(Expected Values)

6. VARIANCE(𝜎2)
• It gives a measure of how the data distributes itself about the
mean.
• It is the average of the squared distance from each point to the
mean.
**Function/ Importance:
• A SMALL VARIANCE indicates that the data points tend to be
very close to the mean.
• A HIGH VARIANCE indicates that the data points are very
spread out from the mean.

7. STANDARD DEVIATION(𝜎)
• Is a measure of dispersion equal to the square root of the
variance.
• Measures the spread of a data distribution.
**Function/ Importance:
• LOW STD DEVIATION means that the most of the numbers are
close to the average.
• HIGH STD DEVIATION means that the numbers are more spread
out.

8. FORMULA
MEAN:
𝜇 = ∑(𝑋 ∙ 𝑃(𝑋))

9. FORMULA
VARIANCE
If Population >> 𝜎2= ∑(𝑋 - 𝜇)2 ∙ 𝑃(𝑋)
OR
If Sample >> 𝜎2 = ∑[𝑋2 ∙ 𝑃(𝑋)] – 𝜇2

10. FORMULA
STANDARD DEVIATION
𝜎 = σ2

11. Example 1: Surgery Patients
The probabilities that a surgeon
operates on patients 3, 4, 5, 6, or 7
in any day are 0.15, 0.10, 0.20, 0.25
and 0.30 respectively. Compute for
the mean, variance and standard
deviation of the random variable.

12. Probability Distribution of Discrete Random Variable
X
Number of Patients 3 4 5 6 7
Probability
P(X)
0.15 0.10 0.20 0.25 0.30

13. SOLUTION: MEAN
Number of Patients (X) 3 4 5 6 7
Probability P(X) 0.15 0.10 0.20 0.25 0.30
𝜇 = ∑(𝑋 ∙ 𝑃(𝑋))
𝜇 = ∑(𝑋 ∙ 𝑃(𝑋))
=3(0.15) + 4(0.10) + 5(0.20) + 6(0.25) + 7(0.30)
=0.45 + 0.4 + 1 + 1.5 + 2.1
𝜇 = 5.45

14. SOLUTION: VARIANCE
Number of Patients (X) 3 4 5 6 7
Probability P(X) 0.15 0.10 0.20 0.25 0.30
𝜎2 = ∑[𝑋2 ∙ 𝑃(𝑋)] – (𝜇2)
𝜎
2
= ∑[𝑋
2
∙ 𝑃(𝑋)] – (𝜇
2
)
= {3
2
(0.15) + 4
2
(0.10) + 5
2
(0.20) + 6
2
(0.25) + 7
2
(0.30)} – (5.45
2
)
= (1.35 + 1.6 + 5 + 9 +14.7) – 29.70
= 31.65 – 29.70
𝜎
2
= 1.95

15. SOLUTION: STANDARD DEVIATION
Number of Patients (X) 3 4 5 6 7
Probability P(X) 0.15 0.10 0.20 0.25 0.30
𝜎 = σ2
𝜎 = 1.95
𝜎 = 1.40

16. MEANING?
Mean = 𝜇 = 5.45
Variance = 𝜎2 = 1.95
Standard Deviation = 𝜎 = 1.40
**Variance is small. It indicates that the data
points tend to be very close to the mean.
**STD Deviation is small. Means that the most of
the numbers are close to the average.

17. X P(X) X • P(X) 𝑿𝟐
• P(X)
1 3/10
6 1/10
11 2/10
16 2/10
21 2/10
Example # 2
Find the mean, variance and standard deviation
of the following probability distribution.

18. X P(X) X • P(X) ∑X • P(X)
1 3/10 1 • 3/10 0.3
6 1/10 6 • 1/10 0.6
11 2/10 11 • 2/10 2.2
16 2/10 16 • 2/10 3.2
21 2/10 21 • 2/10 4.2
Mean (𝜇) 10.5
MEAN

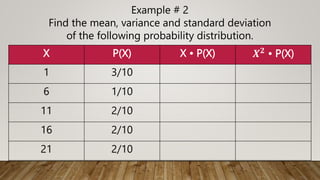
19. X P(X) 𝑿𝟐
• P(X) ∑[𝑋2 ∙ 𝑃(𝑋)]
1 3/10 12
• 3/10 0.3
6 1/10 62
• 1/10 3.6
11 2/10 112
• 2/10 24.2
16 2/10 162
• 2/10 51.2
21 2/10 212
• 2/10 88.2
167.5
𝜎
2 = 167.5 - 10.52
= 57.25
Variance

20. Variance =
𝜎
2 = 57.25
Std Deviation = 𝜎 = σ2
= 57.25
= 7.57

21. Activity:
Answer numbers 1 and 2 in
MODULE 1 (Stat) page 3.