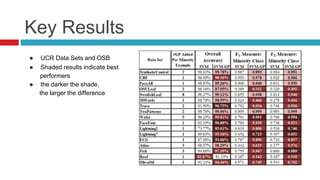
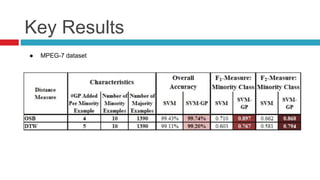
This paper proposes a new technique called "ghost points" to address class imbalance in time series classification problems. Ghost points are synthetic data points generated in the distance space between real data points rather than feature space. The paper defines a methodology to calculate distances between real and ghost points. It tests the approach on 17 time series datasets and an image dataset, finding it significantly improves classification performance over the baselines, especially when used with dynamic time warping and optimal subsequence matching. However, over-sampling adds computational cost and introduces a new parameter around the number of ghost points to generate.

1. Improving SVM classification on imbalanced
time series data sets with ghost points
Presenter: Shang-Tse Chen
Authors: Suzan Köknar-Tezel, Longin Jan Latecki

2. Introduction
● Imbalanced dataset is a challenge for data mining
○ always predict majority class -> high accuracy
○ often, rare events are more interesting
● Common Technique:
○ Up / Down sampling
○ SMOTE (adding synthetic points in feature space)
● This paper
○ adding synthetic points in distance space

3. Research Question
● For time series data
○ not intuitive to represent as features in Rn
○ distance between two sequence is non-metric
○ Cannot use SMOTE
● In many applications, pair-wise distance is more relevant
○ many classifier only need pair-wise distances,
■ eg. SVM, knn
○ many good algorithms to compute distance in time
series data, e.g. DTW, OSB, …, etc.

4. Research Question
● Can we add synthetic data in distance space?
● Does it improve the performance?

5. Methodology
● Given any two points a, b in a distance space X, we can define a
ghost point e = μ(a,b).
● For every x ∈ X, the distance from x to e, d(x, μ(a,b)) is as follows:
○ case 1: {x, a, b} is a metric, then
■ d(x, µ(a, b))2 = ½ d(x, a)2 + ½ d(x, b)2 - ¼ d(a, b)2
○ case 2: If d(a, b) > d(x, a) + d(x, b), then
■ d(x, µ(a, b)) = ½ d(a, b) - d(x, b)
○ case 3a: If d(x, a) > d(x, b) + d(a, b), then
■ d(x, µ(a, b))2 = d(x, b)2 + ¼ d(a, b)2
○ case 3b: If d(x, b) > d(x, a) + d(a, b), then
■ d(x, µ(a, b))2 = d(x, a)2 + ¼ d(a, b)2

6. Data Collection, Processing
● UCR Time series datasets
○ Use 17 datasets from various domains
○ number of classes range from 2 to 50
● MPEG-7
○ 1400 binary images consisting of 70 object classes
○ within each class there are 20 shapes
○ each shape is represented with 100 equidistant sample points on the contour
○ these points are converted into sequences by calculating the curvature of each point with
respect to its five neighbors on each side.
○ this yields 1400 sequences, each of length 100
○ this transformation is invariant to rotation and scale

7. Key Results
● UCR Data Sets and OSB
● Shaded results indicate best
performers
● the darker the shade,
the larger the difference

8. Key Results
● UCR Data Sets and DTW

9. Key Results
● MPEG-7 dataset

10. Summary
● Proposed a new approach for over-sampling the minority
class of imbalanced data
● Unlike other feature based methods, the ghost points
are added in distance space.
● Ghost points can be added to non-metric distance space
○ Can be used with DTW, OSB, and many more.
● Empirical results show significant improvement

11. Critique of work
● For large-scale data, over-sampling is time consuming
● Introduce another parameters, i.e. the number of
ghost points that we should add
● May not perform well in highly noisy data