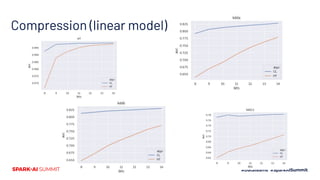
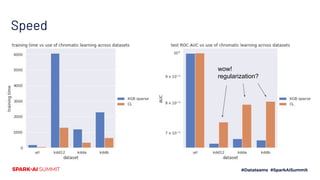
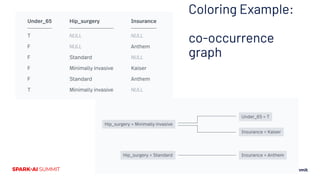
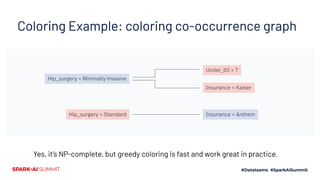
The document presents a novel approach to chromatic sparse learning, focusing on efficiently handling large, sparse datasets in binary classification by employing a graph construction and feature compression methodology. The technique leverages hashing tricks and submodular optimization to reduce dataset dimensions while maintaining classifier quality and allowing for parallel processing. Results indicate significant improvements in dataset compression, facilitating the use of smaller models on modern computational resources.

2. Chromatic Sparse Learning
Vlad Feinberg
Sisu Data
vlad@sisu.ai

3. Outline
Introduction
Methodology
Datasets
Implementation
Results
Conclusion
Technique for sparse data in classification settings.
Not done inside of Spark, but lots of Spark-relevant takeaways.

4. Introduction
Data Expectations
Hashing Trick as a Fair Baseline
Contribution
Related Work

5. Data Expectations
● Large, sparse datasets
● Focus on binary classification
● Less like this
● More like this (but exploded
into a flat, sparse vector)
● Lots of categorical data

6. Data Trends
● JSONB in databases
● Segment, Heap, Fivetran create large analytics tables
● Variable-length set-valued features (lists of posts I liked, things I
retweeted, people I follow, etc.)
● Schema changes often, may not even be fully known
● Schema is large if normalized
● Manual ETL for ML = lots of domain-specific “field work”

7. Structures for your sparse data
● Low-width design matrix
○ Preferably 100s to 1000s of active bits per row (= “nnz”)
● Simplifications
○ Categorical → One-hot “is_CA, is_NV, …”
○ Small counts → unary one-hot “bat [1 time]” “bat [2 times]”
○ Sparse and continuous → bin, one-hot “10K-1M followers”

8. Hashing Trick (HT)
● Weinberger et al 2009 large scale sparse learning
● Mapping 𝜙 from large n to small d
● Split a hash into log d and 1 bits
● “Count-min sketch
with bit flip”
Note “key” j here is int, but is
usually a json key path or word
or bigram (still hashable)

9. How HT Works (Linear Case)
● Large n,
● We would be happy with a linear classifier
● from before is actually a linear map
● Suppose w/ relative error whp
● Then set . By parallelogram law,
● If inner products are preserved:
just learn where
about as good as the real thing

10. How good is the Hashing Trick?
● Hashing trick processes inputs in O(nnz)
● Really fast
● “preserve relative norm” == Johnson-Lindenstrauss property (JL)
● Long body of work:
○ Johnson Lindenstrauss 1984: some projection exists, O(nd) time
○ Alon 2003: need d at least ~1/eps^2
○ Matoušek 2008, Krahmer and Ward 2010: well-behaved (dense) projections have JL
○ Ailon and Chazelle 2009: structured JL projections in O(n lg n + d^3) time
○ Dasgupta, Kumar, Sarlós 2010: HT is a sparse JL matrix, lower bound assumes density
■ Freksen, Kamma, Larsen 2018: Recent tight treatment
● Upshot: HT super fast, but its worst case is sparse data!

11. HT is a strong baseline, but points to possible
improvement
● HT will have JL relative error 𝝐 when
● For bag of words, this holds with 𝝐 = 1/k for at least k-length sentences
● Still works great in practice:

12. Motivation
● Can we take advantage of datasets where nnz per point is small?
● Can this be done in a way that:
#1 does not impact classifier quality?
#2 scales linearly with parallel processing?
● We’ll propose a workflow for handling such datasets and evaluate on
common benchmarks.

13. Contribution
Use an efficient graph construction technique and graph coloring
[1] to shrink datasets from millions of sparse features to 100s of
columns.
Extend a mechanism [2] for categorical feature compression to
featurize effectively. Avoiding so-called target leakage [3] allows high
accuracy with few features.

14. Related Work
● Many individual lines of work are called upon, but these solve more
specific problems and can’t be applied to a general sparse binary
problem:
○ [1] Exclusive Feature Bundling from LGBM (Ke et al 2017)
○ [2] Categorical Feature Compression via Submodular Optimization (Bateni et al 2019)
○ [3] Target leakage from Catboost (Prokhorenkova et al 2018)
● Ultimately, we depend on
the chromatic number of the graph we construct
and submodularity approximations.
● As data-dependent properties
using them enables improvement over HT, which is oblivious.

15. Methodology
Bird’s eye view
Coloring
Submodularity
Intuition

16. Bird’s Eye View: Two Pass Algorithm
● Construct the co-occurrence graph G,
color G, creating 𝜒(G) categorical
variables, associated with each color
● Compress each variable’s values,
mapping multiple similarly-behaving
features to one.
wide but sparse
chi(G)
narrow and dense

17. Coloring
● Sparse data, with low nnz, tends to be mutually exclusive
● Consider a hypothetical medical survey:
○ Multiple-choice questions (“How long ago was your most recent surgery?”) might be represented as binary columns
(surgery_3mo, surgery_12mo, never_had_surgery).
○ All conditional survey sections (“Skip the next section if you are under 65 years old”) will be null when their corresponding
predicates (“Are you under 65 years old?”) are false.
○ And, natural dichotomies may occur: “Who is your employer?” and “Do you use COBRA?”
● Build the graph G with
vertices V for each feature value two vertices are
adjacent if they appear in an example together
(co-occur).

18. Coloring Example:
co-occurrence
graph

19. Coloring Example: coloring co-occurrence graph
Yes, it’s NP-complete, but greedy coloring is fast and work great in practice.

20. Collapse using the color mapping, generating colors as categorical
variables themselves, now shrinking the dataset from 3 columns to 2.
Coloring Example: coloring co-occurrence graph

21. Are we done?
● No. We just “reverse one-hot encoded”
● A speedup for rule-based
classifiers, e.g., GBDTs
● The literature does stop here:
how do we get inputs usable by
LMs, GPs, NNs, FMs?
wide but sparse
chi(G)
narrow and dense
we are
here

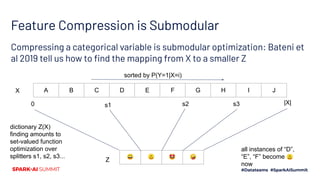
22. Submodular Feature Compression
Detour to Kurkoski and Yagi 2014
View data points as a channel
Encode binary X with multivalue code Y
that “transmits” the label as a message.
But Y might take on lots (M) values. If we
quantize it into a slimmer Z with just K
values, preserve label info with
max_Z I(Z(Y) ; X) [after this slide we’ll go
back to normal lettering, Y is label]
Warning… their X and Y are
flipped from typical ML use

23. Feature Compression is Submodular
Compressing a categorical variable is submodular optimization: Bateni et
al 2019 tell us how to find the mapping from X to a smaller Z
sorted by P(Y=1|X=i)
A B C D E F G H I JX
dictionary Z(X)
finding amounts to
set-valued function
optimization over
splitters s1, s2, s3... 😀 🙃 🤩 🤪
0 |X|s1 s2 s3
Z
all instances of “D”,
“E”, “F” become 🙃
now

24. Global Feature Compression is also Submodular
● Fixes problem if you have multiple categorical variables
● Requires up-front cost of 1 “splitter” per variable
● Then objective = sum of submodular objectives → submodular
X1 X2 X3
Z (one-hot, but now can have
multiple ones in a single row)
P(Y=1|X1) P(Y=1|X2) P(Y=1|X3)

25. Warning: Double Dipping
● Submodular Feature Compression looks at the label
● High-P(Y=1|X) feature values get collapsed together
● If you try to learn on such a feature, you’ll be overconfident
● We propose a quick fix: split the dataset in two!
● Pass 1: Graph structure and coloring
● Pass 2: On half the data, estimate P(Y=1|X). Then compress and learn
on the other half.

26. Intuition
● Why do we expect this to work?
● Erdos-Renyi model: doesn’t require many colors
● G(n, p) random graph with n vertices and edge b/w two vertices wp p
● Achlioptas and Naor 2004: 𝜒(G(n, p)) ~ np log (np)
● Erdos-Renyi isn’t an amazing proxy for the co-occurrence graph but
serves as a baseline where we can approximately equate np with nnz.

27. Datasets
Sparse datasets assessed (thank you to libsvm for curation)
If your feature appears <10%, consider it “sparse”, else “dense”.
For chromatic sparse learning, ignore sparse feature values (implicit
value is just 1.0 for all sparse features). For baseline, keep the
information.
If this worries you, you can use the aforementioned unary encoding.

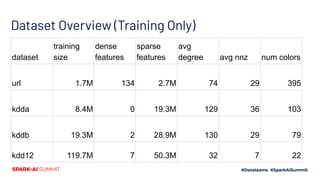
28. URL
● Ma et al 2009
● Sequential data, so train on early days, predict on late [all datasets will
be like this]
● Input: lexical and host-based features of url
● Output: is this a malicious website?

29. KDDA + KDDB
● Yu et al 2010 featurization, Niculescu-Mizil et al 2010 data
● Student interactions in courses (A) and (B) with teaching software
● Input: flattened sequence
of interactions with the
software.
● Output: was the student
able to get the right
answer on their first
attempt?

30. KDD12
● Tencent Weibo is a Twitter-like platform
● Input: User information (who they follow, what they
retweet, what topics they subscribe to)
● Output: Whether the user will follow a recommended topic

31. Dataset Overview (Training Only)
dataset
training
size
dense
features
sparse
features
avg
degree avg nnz num colors
url 1.7M 134 2.7M 74 29 395
kdda 8.4M 0 19.3M 129 36 103
kddb 19.3M 2 28.9M 130 29 79
kdd12 119.7M 7 50.3M 32 7 22

32. Implementation
Top-level overview
Implementation nuggets

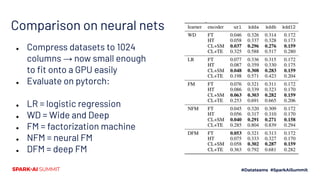
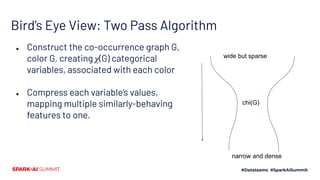
33. Top-level Implementation
● Input format: SVMlight-ish
○ newline-separated [(feature, value)] records
● Coloring
○ Each record is a co-occurence clique
○ Union these into a dataset co-occurence graph
● Color the graph (data-independent)
● Collect P(Y=1|feature)
○ Just some counts for each feature
● Run feature compression (data-independent)
● Recode data
● Note: data-independent != free
wide but sparse
chi(G)
narrow and dense

34. u64 -> u32 Systems Hashing Trick
● Features can be long strings. High memory to track.
● “Systems” HT: Use a u64 hash as the key, map to feature counter u32
● 1B features ~ 2^30
● p(any colliding birthdays) ~ 1 - exp(-2^(-1 - 64 + 30 * 2)) < 3%
● Swiss hash table u64 -> u32 is pretty lean and data-independent
● Do a cheap map-reduce pass to get feature indices going forward

35. Graph Unions
● Each record becomes a clique, then union all records
● Union is commutative and associative
● Basically begging for map-reduce
● Unfortunately, serial merge at
end is killer (my guess for why
“large corpora” are expensive
to build term-to-index maps as
well).

36. Sharded Unions
● Don’t build a single dictionary with map reduce
○ For P processors, E edges, this will have
○ O(P * E) memory usage total
○ O(E * log P) lower bound on runtime due to tree depth of reduce
● Instead, hash join
○ Split hash space (of edges) into P parts
○ Mappers build edges, send to a writer owning that edge’s hash space
○ Writers keep disjoint sets of edges, mutex-guarded
○ Expected contention for a writer is negligible if it’s faster to add to a set than
generate (it is)
● Now O(E + P^2) memory, O(E/P) runtime
● On Malicious URLs, 16 threads:
edge collection 177s → 86s
max rss size 15.7GB → 8.93GB

37. Dataset Splitting
● Can we split data (for feature compression and later training) without
generating a bunch of copies?
● Yes, can do so deterministically and use results across passes.
hash(row) & 1
use for gathering statistics P(Y=1|X) for
feature compression
1
0
use for training ML model

38. Results
● End-to-end compression
● Speed

39. Compression (linear model)

40. Speed
wow!
regularization?

41. Comparison on neural nets
● Compress datasets to 1024
columns → now small enough
to fit onto a GPU easily
● Evaluate on pytorch:
● LR = logistic regression
● WD = Wide and Deep
● FM = factorization machine
● NFM = neural FM
● DFM = deep FM

42. Conclusion
For datasets with a low 𝜒(G), can greatly contract data!
Learned nice nuggets along the way
Systems HT
Sharded Unions / Hash-join reduce
Online Data Splitting to avoid double dip
This is probably just the tip of the iceberg
co-occurrence graph G can be weighted,
promising for deeper exploratory analysis