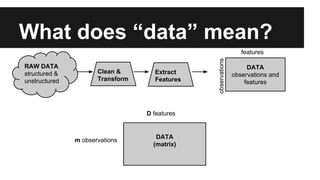
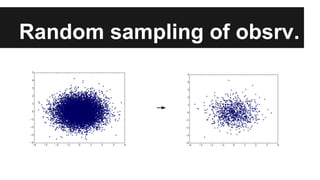
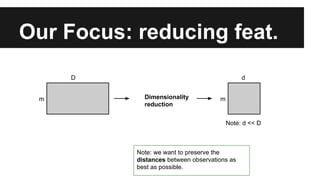
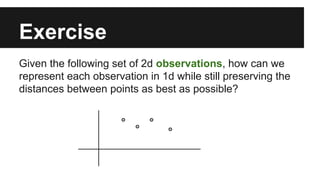
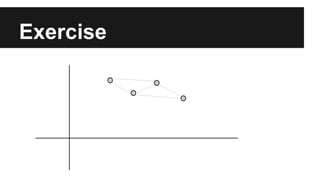
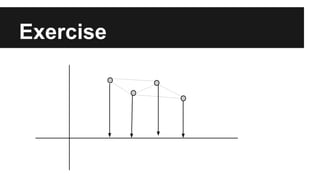
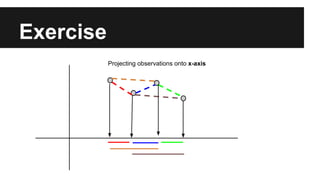
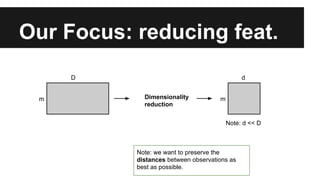
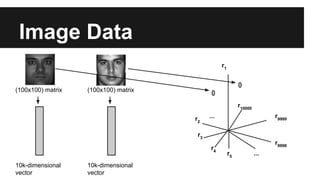
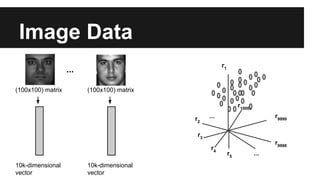
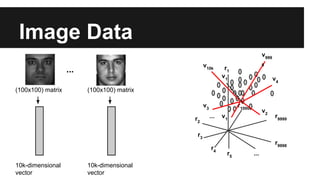
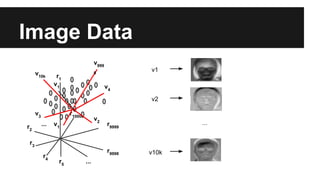
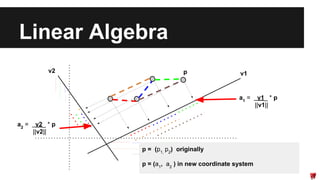
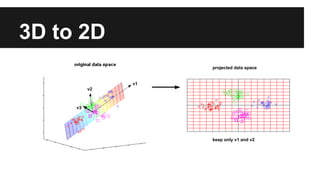
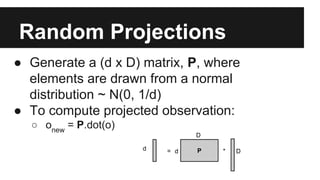
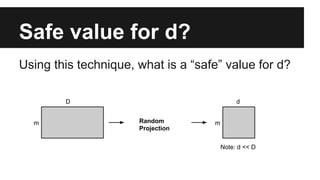
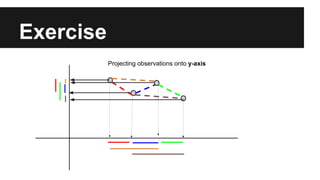
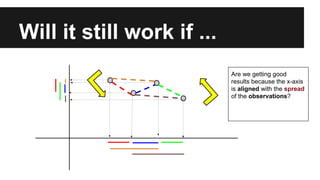
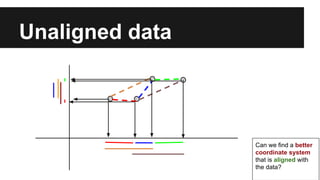
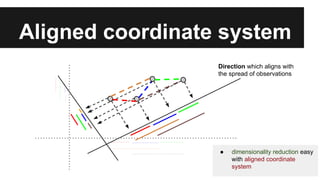
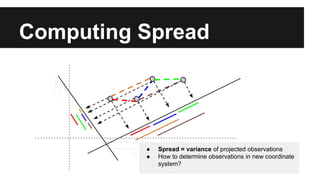
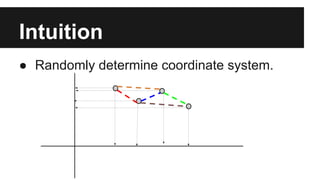
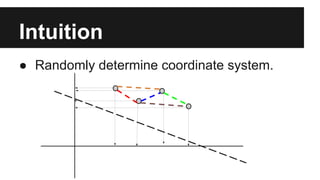
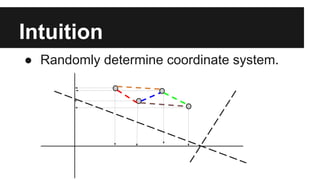
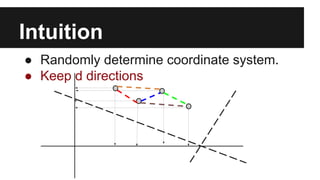
- The document discusses techniques for reducing the size of large datasets ("big data") by reducing the number of observations and features. - Dimensionality reduction techniques like principal component analysis (PCA) and random projections can reduce the number of features to a lower dimensional space while preserving distances between observations. - PCA finds an aligned coordinate system that maximizes the spread of data, while random projections randomly determine a coordinate system. Both techniques can significantly compress datasets, especially those with many redundant features like images.

1. Making BIGDATA
smaller
Tony Tran

2. About Me
● I am from SF
○ SF Bay Area Machine Learning Meetup
○ www.sfdatajobs.com
● Background:
○ BS/MS CompSci (focus on ML/Vision)
○ 4 years as Data Engineer in Ad Tech
○ Currently Consulting

3. What does “data” mean?
RAW DATA
structured &
unstructured
Clean &
Transform
Extract
Features
DATA
observations and
features
observations
features
D features
DATA
(matrix)
m observations

4. What is “Big Data?”
Big data is an all-encompassing term for any collection of data sets so large
and complex that it becomes difficult to process them using traditional data
processing applications -- Wikipedia

5. What is “Big Data?”
Big data is an all-encompassing term for any collection of data sets so large
and complex that it becomes difficult to process them using traditional data
processing applications -- Wikipedia
To me, Big Data is when:
● run out of disc space
● run into “Out Of Memory” Errors
● S3 billing triggers your credit company to call you
● you are willing to go through the pains of setting up a hadoop/spark/etc
cluster (have you tried configuring your own cluster?)

6. Question
● Can we make big data smaller?
● What are the benefits of smaller data?

7. Question
● Can we make big data smaller?
● Benefits of having “small data”:
○ Reduce storage costs
○ Reduce computational costs
○ No more “Out Of Memory” Errors

8. Ideas for making data small
● Reduce the number of observations
○ Only keep observations that are “important”
○ Remove redundant observations
○ Randomly sample
● Reduce the number of features
○ removing non-useful features
○ combining features
○ something clever

9. Random sampling of obsrv.

10. Ideas for making data small
● Reduce the number of observations
○ Only keep rows that are “important”
○ Remove redundant rows
○ Randomly sample
● Reduce the number of features
○ removing non-useful features
○ combining features
○ something clever

11. Our Focus: reducing feat.
m
D
m
d
Dimensionality
Reduction
Note: d << D
Dimensionality
reduction
Note: we want to preserve the
distances between observations as
best as possible.

12. Exercise
Given the following set of 2d observations, how can we
represent each observation in 1d while still preserving the
distances between points as best as possible?

13. Exercise

14. Exercise

15. Exercise
Projecting observations onto x-axis

16. Exercise
Projecting observations onto y-axis

17. Will it still work if ...
Are we getting good
results because the x-axis
is aligned with the spread
of the observations?

18. Unaligned data
Can we find a better
coordinate system
that is aligned with
the data?

19. Aligned coordinate system
Direction which aligns with
the spread of observations
● dimensionality reduction easy
with aligned coordinate
system

20. Computing Spread
● Spread = variance of projected observations
● How to determine observations in new coordinate
system?

21. Linear Algebra
v2 v1
a1 = v1_ * p
||v1||
p
a2 = v2_ * p
||v2||
p = (p1, p2) originally
p = (a1, a2 ) in new coordinate system

22. Observations
● Finding an aligned coordinate system makes
it easy for us to do dimensionality reduction.
○ represent observations in new coordinate system
then remove features (axes).
● The direction parallel to spread of data
maximizes interpoint distances.

23. New tool (PCA)
● How do we find aligned coordinate system?
Is there a tool already developed for this?

24. New tool (PCA)
● How do we find aligned coordinate system?
● Principal Component Analysis
○ Given set of observations, finds an aligned
coordinate system.
○ First direction of coordinate system will contain the
most spread, followed by the second, so forth.
○ O(m3) runtime

25. PCA (scikit-learn)
>>> X = … data matrix of size (m x D) ...
>>> from sklearn.decomposition import PCA
>>>
>>> pca = PCA(n_components=d)
>>> pca.fit(X) # fits new coordinate system to data
>>> pca.transform(X) # transforms data to new coordinate
# system and removes dimensions
>>>> gives us matrix of size (m x d)

26. Our Focus: reducing feat.
m
D
m
d
Dimensionality
Reduction
Note: d << D
Dimensionality
reduction
Note: we want to preserve the
distances between observations as
best as possible.

27. 3D to 2D
v1
v2
v3
projected data space
keep only v1 and v2

28. Image Data
● What if our data is images? How do we
represent an image as an observation?
(100x100) matrix

29. Images and vectors
(100x100) matrix
10k-dimensional
vector

30. Image Data
(100x100) matrix
10k-dimensional
vector
(100x100) matrix
10k-dimensional
vector
r3
r1
r2
r4 r5 ...
r9999
r9998
r10000
...

31. Image Data
(100x100) matrix
10k-dimensional
vector
(100x100) matrix
10k-dimensional
vector
r3
r1
r2
r4 r5 ...
r9999
r9998
r10000
...
...

32. Image Data
(100x100) matrix
10k-dimensional
vector
(100x100) matrix
10k-dimensional
vector
r3
r1
r2
r4 r5 ...
r9999
r9998
r10000
...
...
v999
9
v4
v2
v1
v10k
v1
v3

33. Image Data
v1
v2
v10k
...
r3
r1
r2
r4 r5 ...
r9999
r9998
r10000
...
v999
9
v4
v2
v1
v10k
v1
v3

34. Image Data

35. Image Data
= a1 + a2 +…+ a10k
Original Image

36. Image Data
= a1 + a2 +…+ a10k
Original Image
= a1 + …+ a20
reconstruct with 20 directions

37. Image Data
= a1 + a2 +…+ a10k
Original Image
= a1 + …+ a20
reconstruct with 20 directions
= a1 + …+ a90
reconstruct with 90 directions

38. Image Data
= a1 + a2 +…+ a10k
Original Image
= a1 + …+ a90
reconstruct with 90 directions
Compression!
Each image can now be represented by 90 weights!

39. Image Data
= a1 + …+ a90
reconstruct with 90 directions
● original image representation: 10k values
● compression requires:
○ 90 direction vectors = (90 x 10k values)
○ 1 image = 90 weights (for the direction vectors)

40. Image Data
= a1 + …+ a90
reconstruct with 90 directions
● For 200 images:
○ original representation: 200*10k
○ compression: (90x10k) + 200*90

41. Image Data
= a1 + …+ a90
reconstruct with 90 directions
● For 200 images:
○ original representation: 200*10k
○ compression: (90x10k) + 200*90
makes sense to use this
compression technique when
we have more than 90 images
to compress

42. Keep in mind
● O(m3) runtime
● Need to keep around d directions of length D to
perform projection.
● Requires to be able to read in data to memory.
● What if data is non-linear?

43. Random Projections
● Generate a (d x D) matrix, P, where
elements are drawn from a normal
distribution ~ N(0, 1/d)
● To compute projected observation:
○ onew = P.dot(o)
D
d = d P
* D

44. Intuition
● Randomly determine coordinate system.

45. Intuition
● Randomly determine coordinate system.

46. Intuition
● Randomly determine coordinate system.

47. Intuition
● Randomly determine coordinate system.
● Keep d directions

48. Safe value for d?
Using this technique, what is a “safe” value for d?
m
D
m
d
Dimensionality
Reduction
Note: d << D
Random
Projection

49. Safe value for d?
>> from sklearn.random_projection import johnson_lindenstrauss_min_dim
def johnson_lindenstrauss_min_dim(n_observations,eps=0.1):
● input:
○ n_observations -- the number of observations you have
○ eps -- the amount of error you’re willing to tolerate
● output:
○ safe number of features that you can project down to

50. Mathematical Guarantees
Original distance
Projected distance
d >= 4 log(m) / (eps^2 / 2 - eps^3 / 3)

51. Practical usage
● High probability that projection will be good,
but there’s still a chance that it will not be!
○ Create multiple projections and test guarantees with
sampled observations.

52. Comparison
● PCA
○ finds aligned coordinate system which maximizes spread.
○ o(m3) runtime + requires all points to be read into memory.
○ o(dD) space to store aligned coordinate system for projection.
● Random Projection
○ finds random coordinate system
○ o(dD) runtime and space to construct projection Matrix
○ Guaranteed with high probability to work

53. Thank you
Tony Tran
tony@sfdatajobs.com
@quicksorter

54. References
● http://www.cs.princeton.edu/~cdecoro/eigenfaces/
● http://scikit-learn.org/stable/modules/generated/sklearn.
decomposition.PCA.html#sklearn.decomposition.PCA
● http://scikit-learn.org/stable/modules/random_projection.
html
● http://blog.yhathq.com/posts/sparse-random-projections.
html