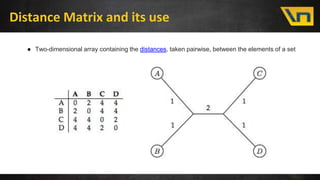
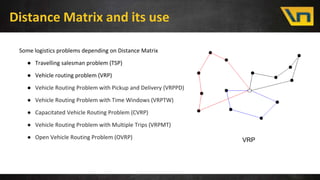
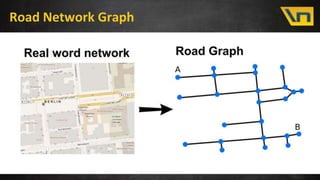
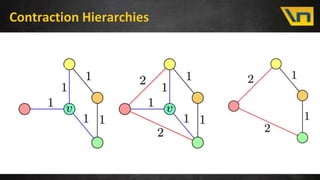
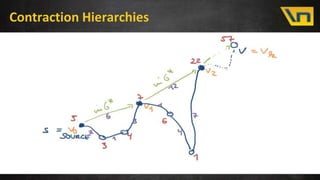
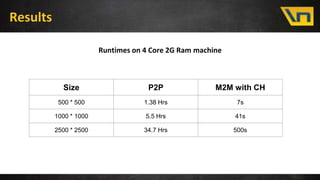
This document discusses fast distance matrix computation using contraction hierarchies. It begins with an overview and introduction to distance matrices and their uses in logistics problems. It then discusses standard graph algorithms like Dijkstra's algorithm and bidirectional Dijkstra. Challenges with naive algorithms are presented, including large search spaces. Contraction hierarchies are then introduced as a technique to preprocess the graph to reduce the search space for queries. With contraction hierarchies, the number of explored nodes is reduced dramatically, leading to much faster computation of distance matrices. Results show improvements from hours to seconds for larger problem sizes.

1. Fast Distance Matrix Computation
using
Contraction Hierarchies
By
Vikas Veshishth Gargay
Geo Intelligence Team

2. Overview
1. Distance matrix and its use
2. Some well known problems which use distance matrix
3. Road Network Graph
4. Basic Graph algorithms
5. Algorithms for Distance Matrix
6. Challenges !
7. Contraction Hierarchies
8. Improved Distance Matrix computation
9. Results
10. References
11. Questions

3. Distance Matrix and its use
● Two-dimensional array containing the distances, taken pairwise, between the elements of a set

4. Distance Matrix and its use
Some logistics problems depending on Distance Matrix
● Travelling salesman problem (TSP)
● Vehicle routing problem (VRP)
● Vehicle Routing Problem with Pickup and Delivery (VRPPD)
● Vehicle Routing Problem with Time Windows (VRPTW)
● Capacitated Vehicle Routing Problem (CVRP)
● Vehicle Routing Problem with Multiple Trips (VRPMT)
● Open Vehicle Routing Problem (OVRP) VRP

5. Road Network Graph

6. 1.Basic Graph algorithms
1 function Dijkstra(Graph, source):
2 dist[source] ← 0 // Initialization of MST
3
4 create vertex set Q
5
6 for each vertex v in Graph:
7 if v ≠ source
8 dist[v] ← INFINITY // Unknown distance from source to v
9 prev[v] ← UNDEFINED // Predecessor of v
10
11 Q.add_with_priority(v, dist[v])
12
13
14 while Q is not empty: // The main loop
15 u ← Q.extract_min() // Remove and return best vertex
16 for each neighbor v of u: // only v that is still in Q
17 alt = dist[u] + length(u, v)
18 if alt < dist[v]
19 dist[v] ← alt
20 prev[v] ← u
21 Q.decrease_priority(v, alt)
22
23 return dist[], prev[]
Dijkstra

7. Basic Graph algorithms
● Alternate between forward and
backward dijkstra search from s and t
respectively
● Stop when settling a node that is
already settled in the other Dijkstra
● Observe : That node settled by both
searches is not necessarily on the SP
The cost of the shortest path is then :
min {dist s[u] + dist t[u] : for all u visited
in both}
Bidirectional Dijkstra

8. Algorithms for Distance Matrix
P2P algorithm :
● Run Dijkstra’s Algorithm for every source and target node
● Dijkstra’s Algorithm is repeated over same portions of search space
● O (S * T dijkstras) time
One to many dijkstra :
● Run Dijkstra’s Algorithm for every source to all target nodes
● Dijkstra’s Algorithm is repeated over same portions of search space
● Computation time increases much faster as the search radius increases and more nodes are added
● O(S dijkstras) time

9. Algorithms for Distance Matrix

10. Algorithms for Distance Matrix
Bidirectional Many-to-Many Algorithm with Bucketing

11. Algorithms for Distance Matrix
Bucket data structure
}

12. Algorithms for Distance Matrix
Complexity for many to many with bucketing
● Time complexity is order of | S + T | dijkstras
– Plus going through ALL nodes explored from both sides !
● Space consumed is HUGE !
– Each bucket has O(T) space
– Each node has a bucket
– There are 1,00,000 nodes searched for an average point to point search in a
20km radius

13. Challenges!
● P2P distance matrix algorithm takes less space but huge time
● One to many is theoretically slow
● Many to many algorithm should be fast but is slowed down by huge search space
– Search space can be reduced by tracking reached nodes in priority queue but with caveats
Runtimes on 4 Core 2G Ram machine
Size P2P
500 * 500 1.38 Hrs
1000 * 1000 5.5 Hrs

14. Challenges!
● How to recover ?
– Break m * n into parallel m/2 * n/2 calls
– Use a distributed framework , spark, etc to separate out the forward
searches
– Increase Heap size
– Use one to many
● Or solve the problem at root , decrease search space
but how ?

15. Contraction Hierarchies

16. Contraction Hierarchies
Contraction of a single node
● This is the basic building block of the CH precomputation
– Idea: take out a node, and add all necessary arcs such that all SP distances in the
remaining graphs are preserved
– Formally, a node v is contracted as follows
• Let {u1,...,ul} be the incoming arcs, i.e. (ui, v) ϵ E
• Let {w1,...,wk} be the outgoing arcs, i.e. (v, wj) ϵ E
• For each pair {ui, wj }, if (ui, v, wj) is the only shortest path from ui to wj, add
the shortcut arc (ui, wj )
• Then remove v and its adjacent arcs from the graph

17. Contraction Hierarchies

18. Contraction Hierarchies
Query
● Given G* = (V, E*) and a source s and a target t
● Define the upwards graph G* = (V, {(u, v) ϵ E* : v > u})
● Define the downwards graph Gb* = (V, {(u, v) ϵ E* : v < u}) : v < u})
● Do a full Dijkstra computation from s forwards in G*
● Do a full Dijkstra computation from t backwards in Gb*
● Let I be the set of nodes settled in both Dijkstras
● Take dist(s, t) =min {dist(s, v) + dist(v, t) : v ϵ I}

19. Contraction Hierarchies
●Why it works ?
●How is node ordering chosen?

20. Contraction Hierarchies

21. Improved Distance Matrix computation
●Used the processed graph
●Reduced the number of explored nodes in search
space
●From 1,00,000 to 1000 nodes on average
●Reduced heavily the space and hence computation
time over nodes.

22. Results
Runtimes on 4 Core 2G Ram machine
Size P2P M2M with CH
500 * 500 1.38 Hrs 7s
1000 * 1000 5.5 Hrs 41s
2500 * 2500 34.7 Hrs 500s

23. References
Most Images/material are from :
● https://en.wikipedia.org/wiki/Distance_matrix
● http://rosalind.info/media/distance_based_phylogeny.png
● https://en.wikipedia.org/wiki/Vehicle_routing_problem
● http://2014.berlinbuzzwords.de/sites/2014.berlinbuzzwords.de/files/media/documents/peter_karich_-
_how_we_made_graphhopper_scale.pdf
● http://www.redblobgames.com/pathfinding/a-star/introduction.html
● http://www.cc.gatech.edu/~thad/6601-gradAI-fall2014/02-search-01-Astart-ALT-Reach.pdf
● http://i11www.iti.uni-karlsruhe.de/_media/teaching/theses/files/da-sknopp-06.pdf
● http://algo2.iti.kit.edu/schultes/hwy/distTableSlides.pdf
● http://algo2.iti.kit.edu/download/algeng-workshop-google-routing.pdf
● http://ad-teaching.informatik.uni-freiburg.de/route-planning-ss2012/lecture-7.pdf
● http://algo2.iti.kit.edu/schultes/hwy/contract.pdf

24. Questions
?
[ e-mail : vikas.v.iitr@gmail.com ]

25. Thank You