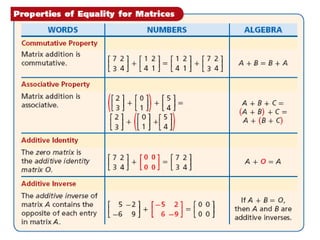
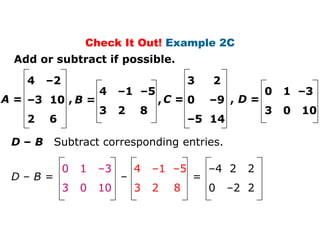
The document provides a lesson on matrices and matrix operations including addition, subtraction, and scalar multiplication of matrices. It begins with examples of displaying data in matrix form and finding entries, dimensions, and addresses of matrices. It then covers adding and subtracting matrices if they have the same dimensions, as well as multiplying matrices by scalars. The document concludes with examples of simplifying matrix expressions and a quiz to assess understanding.

1. Matrices and Data
Warm Up
Lesson Presentation
Lesson Quiz

2. Warm Up
Distribute.
1. 3(2x + y + 3z) 6x + 3y + 9z
2. –1(x – y + 2) –x + y – 2
State the property illustrated.
3. (a + b) + c = a + (b + c)
Associative Property of Addition
4. p + q = q + p
Commutative Property of Addition

3. Objectives
Use matrices to display mathematical
and real-world data.
Find sums, differences, and scalar
products of matrices.

4. Vocabulary
matrix
dimensions
entry
address
scalar

5. Matrix A has two rows and three columns. A matrix
with m rows and n columns has dimensions m
n, read “m by n,” and is called an m n matrix. A has
dimensions 2 3. Each value in a matrix is called an
entry of the matrix.

6. The address of an entry is its location in a matrix,
expressed by using the lower case matrix letter with
row and column number as subscripts. The score
16.206 is located in row 2 column 1, so a21 is 16.206.

7. Example 1: Displaying Data in Matrix Form
6 in 9 in
The prices for different
Roast beef $3.95 $5.95
sandwiches are
Turkey $3.75 $5.60
presented at right.
Tuna $3.50 $5.25
3.95 5.95
A. Display the data in
matrix form. P = 3.75 5.60
3.50 5.25
B. What are the dimensions of P?
P has three rows and two columns, so it is a 3 2
matrix.

8. Example 1: Displaying Data in Matrix Form
6 in 9 in
The prices for different
Roast beef $3.95 $5.95
sandwiches are
Turkey $3.75 $5.60
presented at right.
Tuna $3.50 $5.25
C. What is entry P32? What does it represent?
The entry at P32, in row 3 column 2, is 5.25. It is
the price of a 9 in. tuna sandwich.
D. What is the address of the entry 5.95?
The entry 5.95 is at P12.

9. Check It Out! Example 1
Use matrix M to
answer the
questions below.
a. What are the dimensions of M? 3 4
b. What is the entry at m32? 11
c. The entry 0 appears at what two addresses?
m14 and m23

10. You can add or subtract two matrices only
if they have the same dimensions.

11. Example 2A: Finding Matrix Sums and Differences
Add or subtract, if possible.
3 –2 4 7 2 1 4 2 –2 3
W= ,X= , Y= , Z=
1 0 5 1 –1 –2 3 1 0 4
W+Y
Add each corresponding entry.
3 –2 1 4 3+1 –2 + 4 4 2
W+Y= + = =
1 0 –2 3 1 + (–2) 0+3 –1 3

12. Example 2B: Finding Matrix Sums and Differences
Add or subtract, if possible.
3 –2 4 7 2 1 4 2 –2 3
W= ,X= , Y= , Z=
1 0 5 1 –1 –2 3 1 0 4
X–Z
Subtract each corresponding entry.
4 7 2 2 –2 3 2 9 –1
X–Z= – =
5 1 –1 1 0 4 4 1 –5

13. Example 2C: Finding Matrix Sums and Differences
Add or subtract, if possible.
3 –2 4 7 2 1 4 2 –2 3
W= ,X= , Y= , Z=
1 0 5 1 –1 –2 3 1 0 4
X+Y
X is a 2 3 matrix, and Y is a 2 2 matrix.
Because X and Y do not have the same dimensions,
they cannot be added.

14. Check It Out! Example 2A
Add or subtract if possible.
4 –2 3 2
4 –1 –5 0 1 –3
A = –3 10 , B = ,C = 0 –9 , D =
3 2 8 3 0 10
2 6 –5 14
B+D Add each corresponding entry.
B+D=
4 –1 –5 0 1 –3 44+ 0 –8 + 1 –5 + (–3)
0 –1
+ =
3 2 8 3 0 10 36+ 3
2 18
2+0 8 + 10

15. Check It Out! Example 2B
Add or subtract if possible.
4 –2 3 2
4 –1 –5 0 1 –3
A = –3 10 , B = ,C = 0 –9 , D =
3 2 8 3 0 10
2 6 –5 14
B–A
B is a 2 3 matrix, and A is a 3 2 matrix.
Because B and A do not have the same
dimensions, they cannot be subtracted.

16. Check It Out! Example 2C
Add or subtract if possible.
4 –2 3 2
4 –1 –5 0 1 –3
A = –3 10 , B = ,C = 0 –9 , D =
3 2 8 3 0 10
2 6 –5 14
D–B Subtract corresponding entries.
0 1 –3 4 –1 –5 –4 2 2
D–B= – =
3 0 10 3 2 8 0 –2 2

17. You can multiply a matrix by a number, called a scalar.
To find the product of a scalar and a matrix, or the
scalar product, multiply each entry by the scalar.

18. Example 3: Business Application
Use a scalar Shirt Prices
product to find T-shirt Sweatshirt
the prices if a Small $7.50 $15.00
10% discount is Medium $8.00 $17.50
applied to the Large $9.00 $20.00
prices above. X-Large $10.00 $22.50
You can multiply by 0.1 and subtract from the
original numbers.
7.5 15 7.5 15 6.75 15
7.5 13.50
0.75 1.5
8 17.5 7.20 17.5
15.75
– 0.1 8 17.5
= 8
– 0.8 1.75
9 20 9 20 8.10 20
9 18.00
0.9 2
10 22.5 10 22.5 9.00 22.5
10 20.25
1 2.25

19. Example 3 Continued
The discount prices are shown in the table.
Discount Shirt Prices
T-shirt Sweatshirt
Small $6.75 $13.50
Medium $7.20 $15.75
Large $8.10 $18.00
X-large $9.00 $20.25

20. Check It Out! Example 3
Use a scalar product Ticket Service Prices
to find the prices if a Days Plaza Balcony
20% discount is 1—2 $150 $87.50
applied to the ticket 3—8 $125 $70.00
service prices.
9—10 $200 $112.50
You can multiply by 0.2 and subtract from the
original numbers.
150 87.5 150 87.5 150 87.5
120 70 30 17.5
125 70 – 0.2 125 70 = 125 70
100 56 – 25 14
200 112.5 200 112.5 200 112.5
160 90 40 22.5

21. Check It Out! Example 3 Continued
Discount Ticket Service Prices
Days Plaza Balcony
1—2 $120 $70
3—8 $100 $56
9—10 $160 $90

22. Example 4A: Simplifying Matrix Expressions
3 –2 1 4
4 7 2
P= 1 0 Q= R = –2 3
5 1 –1
2 –1 0 4
Evaluate 3P — Q, if possible.
P and Q do not have the same dimensions; they
cannot be subtracted after the scalar products are
found.

23. Example 4B: Simplifying Matrix Expressions
3 –2 1 4
4 7 2
P= 1 0 Q= R = –2 3
5 1 –1
2 –1 0 4
Evaluate 3R — P, if possible.
1 4 3 –2 3 0 14
3(1)123(4) 3 –2 –2
3
= 3 –2 3 – 1 0 = 3(–2) 9 – –
–6 9 3(3) 1
–7 0
1 0
0 4 2 –1 0 –2 13
3(0)123(4) 2 –1 –1
2

24. Check It Out! Example 4a
4 –2 4 –1 –5 3 2
A= B= C= D = [6 –3 8]
–3 10 3 2 8 0 –9
Evaluate 3B + 2C, if possible.
B and C do not have the same dimensions; they
cannot be added after the scalar products are found.

25. Check It Out! Example 4b
4 –2 4 –1 –5 3 2
A= B= C= D = [6 –3 8]
–3 10 3 2 8 0 –9
Evaluate 2A – 3C, if possible.
4 –2 3 2 2(4) 2(–2) –3(3) –3(2)
=2 –3 = +
–3 10 0 –9 2(–3) 2(10) –3(0) –3(–9)
8 –4 –9 –6 –1 –10
= + =
–6 20 0 27 –6 47

26. Check It Out! Example 4c
4 –2 4 –1 –5 3 2
A= B= C= D = [6 –3 8]
–3 10 3 2 8 0 –9
Evaluate D + 0.5D, if possible.
= [6 –3 8] + 0.5[6 –3 8]
= [6 –3 8] + [0.5(6) 0.5(–3) 0.5(8)]
= [6 –3 8] + [3 –1.5 4]
= [9 –4.5 12]

28. Lesson Quiz
1. What are the dimensions of A? 3 2
2. What is entry D12? –2
Evaluate if possible.
3. 2A — C 4. C + 2D 5. 10(2B + D)
Not possible